
3.主链含5个碳原子,有甲基、乙基2个支链的烷烃有 ( )
A 2种 B 3种 C 4种 D 5种
2.下列说法正确的是 ( )
A.凡是分子组成相差一个或若干个“CH2”原子团的物质,彼此一定是同系物
B.相对分子质量相同的物质,互称同分异构体
C. 化学性质相似的物质是同系物
D.相对分子质量相同,组成元素的质量分数相同的不同有机物一定是同分异构体
1.2005年1月,欧洲航天局的惠更斯号探测器首次成功登陆土星的最大卫星--土卫六。科学家对探测器发回的数据进行了分析,发现土卫六的大气层中含有95%的氮气,剩余的气体为甲烷和其它碳氢化合物。下列关于碳氢化合物的叙述正确的是 ( )
A.碳氢化合物的通式为CnH2n+2 B.石油的主要成分是碳氢化合物
C.乙炔是含碳量最高的碳氢化合物 D.碳氢化合物中的化学键都是极性键
21.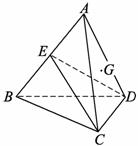
(1) 证明:∵BC=AC,E为AB的中点,∴AB⊥CE.
又∵AD=BD,E为AB的中点∴AB⊥DE. ∵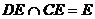
∴AB⊥平面DCE∵AB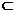 平面ABC,∴平面CDE⊥平面ABC.
平面ABC,∴平面CDE⊥平面ABC.
(2)∵在△BDC中,DC=3,BC=5,BD=4,∴CD⊥BD,
在△ADC中,DC=3,AD=BD=4,AC=BC=5,∴CD⊥AD,
∵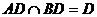 ∴CD⊥平面ABD.所以线段CD的长
∴CD⊥平面ABD.所以线段CD的长
是三棱锥C-ABD的高。…………6分
又在△ADB中,DE=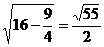 ∴VC-ABD=
∴VC-ABD=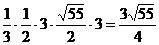
(3)在AB上取一点F,使AF=2FE,则可得GF∥平面CDE
取DC的中点H,连AH、EH
∵G为△ADC的重心,∴G在AH上,且AG=2GH,连FG,则FG∥EH
又∵FG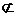 平面CDE, EH
平面CDE, EH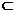 平面CDE,∴GF∥平面CDE
平面CDE,∴GF∥平面CDE
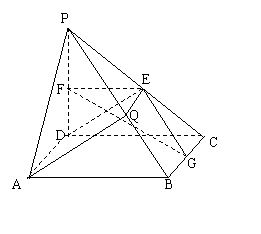
20. (1)证明:∵PE=EC,PF=FD∴EF∥CD,CD∥AB,∴EF∥AB
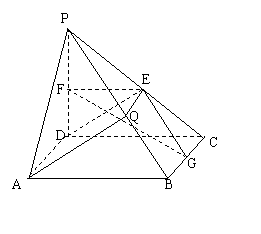 ∴EF∥平面PAB,同理EG∥平面PAB. 又∵EF∩EG=E
∴EF∥平面PAB,同理EG∥平面PAB. 又∵EF∩EG=E
∴平面PAB∥平面EFG,而PA在平面PAB内,
∴PA∥平面EFG。
(2)取PB中点为Q,则Q满足题意。
证明:由中点可知: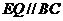 ,而
,而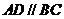 ,
,
∴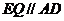 ,∴A、D、E、Q四点共面。
,∴A、D、E、Q四点共面。
∵CD⊥AD,面PDC⊥面ABCD于CD,AD在平面ABCD内,
∴AD⊥平面PDC,AD⊥PC又PD=DC, ∠PDC=
∠PDC=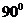
∴△PDC为等腰直角三角形,
∵PE=EC, ∴DE⊥PC,AD∩DE=D,
∴PC⊥面ADEQ∴Q为PB的中点时,PC⊥面ADQ
19. 解 如图
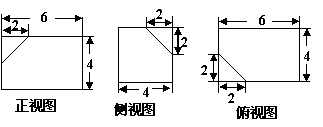
(2)解 所求多面体的体积
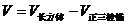
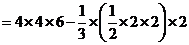 =
=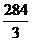 (cm3).
(cm3).
 (3)证明 如图(2),在长方体
(3)证明 如图(2),在长方体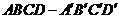 中,
中,
连结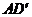 ,则
,则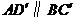 .
.
因为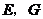 分别为
分别为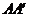 ,
,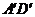 的中点,
的中点,
所以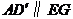 ,
,
从而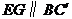 .又
.又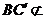 平面
平面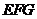 ,
,
所以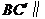 面
面 .
.
18. (1)解 由CE=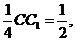
∴VC-BDE=VE-BCD=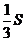 △BCD·CE=
△BCD·CE=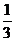 ×
×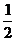 ×1×1×
×1×1×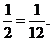
(2)证明连结AC、B1C
∵AB=BC,∴BD⊥AC.
∵A1A⊥底面ABCD,∴BD⊥A1A.
∵A1A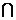 AC=A,∴BD⊥平面A1AC.
AC=A,∴BD⊥平面A1AC.
∴BD⊥A1C
∴tan∠BB1C=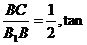 ∠CBE=
∠CBE=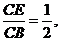 ∴∠BB1C=∠CBE.
∴∠BB1C=∠CBE.
∵∠BB1C+∠BCB1=90°,∴∠CBE+∠BCB1=90°.∴BE⊥B1C
∵BE⊥A1B1,A1B1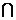 B1C=B1,∴BE⊥平面A1B1C.∴BE⊥A1C.
B1C=B1,∴BE⊥平面A1B1C.∴BE⊥A1C.
∵BD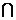 BE=B,BE
BE=B,BE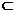 平面BDE,BD
平面BDE,BD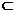 平面BDE,∴A1C⊥平面BDE.
平面BDE,∴A1C⊥平面BDE.
17. 证明:(1)连CD1交CD1于O点,连OE
因为O是CD1的中点,所以OE∥BD1,所以BD1∥平面C1DE。
(2)过B1点作B1P⊥C1E,交CC1于P点。在正方形BCC1B1中,易证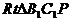 ≌
≌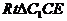 ,得P是CC1的中点。
,得P是CC1的中点。
因为A1B1⊥平面B1C,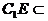 平面B1C
平面B1C
所以A1B1⊥C1E
又因为C1E⊥B1P,所以C1E⊥平面A1B1P
所以平面A1B1P⊥平面C1DE
故取CC1的中点P,就有平面A1B1P⊥平面C1DE
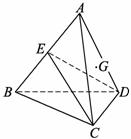
21.如图,已知,在空间四边形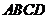 中,
中,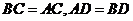 ,
,
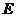 是
是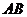 的中点.
的中点.
(1)求证:平面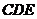 ⊥平面
⊥平面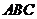 ;
;
(2)若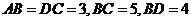 ,求几何体
,求几何体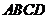 的体积;
的体积;
(3)若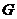 为△
为△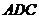 的重心,试在线段
的重心,试在线段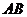 上找一点
上找一点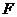 ,使得
,使得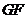 ∥平面
∥平面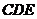 .
.
ADCDA BCCCC 11. 2 12.6 13. 60o 14. 1+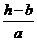 15. 0<a<
15. 0<a<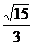 16.①②④
16.①②④
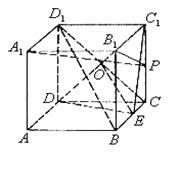
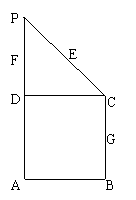
20.如下图所示,在直角梯形ABCD中,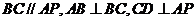 ,
,
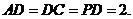
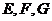 分别为线段
分别为线段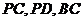 的中点,现将
的中点,现将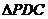 折起,使平面
折起,使平面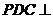 平面
平面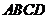 。
。
(1)求证: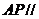 平面
平面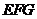 ;
;
(2)在线段PB上确定一点Q,使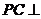 平面
平面 试给出证明。
试给出证明。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com