
(1)计算: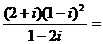 ( )
( )
(A)2 (B)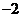 (C)
(C)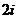 (D)
(D)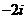
(2)已知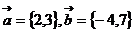 ,则
,则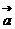 在
在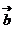 上的射影为
上的射影为
(A) 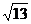 ; (B)
; (B) 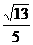 ; (C)
; (C) 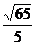 ; (D)
; (D) 
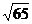
(3)已知a、b为直线,α、β为平面.在下列四个命题中,
① 若a⊥α,b⊥α,则a∥b ; ② 若 a∥α,b ∥α,则a∥b;
③ 若a⊥α,a⊥β,则α∥β; ④ 若α∥b,β∥b ,则α∥β.
正确命题的个数是
(A) 1 (B) 3 (C) 2 (D) 0
(4)函数f(x)=A·tan(ωx+φ)(φ>0)在区间[m,n]上的函数值都小于0,则函数g(x)=A·cot(ωx+φ)在[m,n]上的函数值
(A) 都大于0,且有最大值为g(m) (B) 都小于0,且有最大值为g(m)
(C) 都大于0,且有最小值为g(m) (D) 都小于0,且有最小值为g(m)
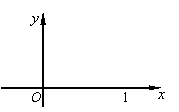 (5)已知函数
(5)已知函数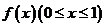 的图象的一段圆弧(如图所示)
的图象的一段圆弧(如图所示)
若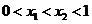 ,则
,则
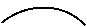 (A)
(A)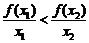 (B)
(B)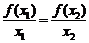
(C)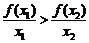 (D)前三个判断都不正确
(D)前三个判断都不正确
(6)对于四条曲线:① 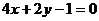 ;②
;② 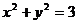 ;③
;③ 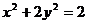 ;
;
④ 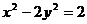 . 其中与直线2 x + y +3=0有交点的所有曲线是
. 其中与直线2 x + y +3=0有交点的所有曲线是
(A) ②,③,④ (B) ①,② (C) ②,④ (D) ①,②,③
(7)将4名司机和8名售票员分配到四辆公共汽车上,每辆车上分别有1名司机和2名售票员,则可能的分配方案种数是
(A)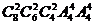 (B)
(B)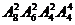 (C)
(C)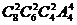 (D)
(D)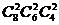
(8)定义在R上的偶函数f(x)在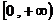 上递增,
上递增,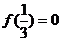 ,则满足
,则满足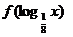 >0的x的取值范围是
>0的x的取值范围是
(A)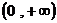 (B)
(B)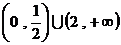 (C)
(C) 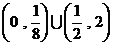 (D)
(D) 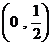
(9)现有一个长方体水箱,从水箱里面量得它的深是30cm,底面的长是25cm,宽是20cm.设0< a ≤8,水箱里盛有深为a cm的水,若往水箱里放入棱长为10cm的立方体铁块,则水深为
(A) 2 cm
(B) 10 cm
(C) (a+2) cm
(D) 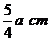
(10)我国首航员杨利伟乘坐的“神舟五号”载人宇宙飞船的运行轨道是以地球的中心F为一个焦点的椭圆,近地点A距地面为m公里,远地点B距地面为n公里.若地球的半径为R公里,则飞船运行轨道的短轴长为
(A) mn (B) 2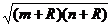 (C) 2nm (D)
(C) 2nm (D) 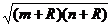
(11)已知函数f(x)的图象过点(0,-5),它的导数f /(x)=4x3-4x,则当f(x)取得最大值-5时,x的值应为
(A) -1 (B) 0 (C) 1 (D) ±1
(12)在平面直角坐标系中,有两个区域M、N,M是由三个不等式y≥0、y≤x和y≤2-x确定的;N是随t变化的区域,它由不等式t≤x≤t+1(0≤t≤1)所确定.设M、N的公共部分的面积为f(t),则f(t)等于
(A)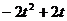 (B)
(B)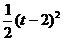 (C)
(C)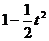 (D)
(D) 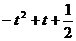
(17)(本小题満分12分)
设一部机器在一天内发生故障的概率为0.2,机器发生故障时全天停止工作.若一周5个工作日里均无故障,可获利润10万元;发生一次故障可获利润5万元,只发生两次故障可获利润0万元,发生三次或三次以上故障就要亏损2万元.求一周内期望利润是多少?
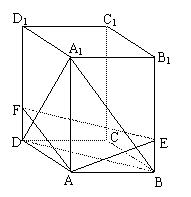 (18)(本小题满分12分)
(18)(本小题满分12分)
正四棱柱ABCD-A1B1C1D1的底面边长是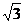 ,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
(Ⅰ)求证:A1C⊥面AEF;
(Ⅱ)求截面AEF与底面ABCD所成的二面角的大小;
(Ⅲ)求点B到面AEF的距离.
(19)(本小题満分12分)
若数列{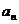 }的通项
}的通项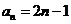 ,设数列{
,设数列{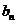 }的通项
}的通项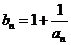 ,又记
,又记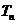 是数列{
是数列{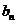 }
}
的前n项的积.
(Ⅰ)求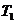 ,
,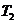 ,
,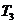 的值;
的值;
(Ⅱ)试比较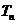 与
与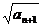 的大小,并证明你的结论.
的大小,并证明你的结论.
(20)(本小题満分12分)
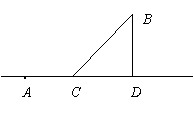 如图,有甲乙两个村庄,甲村位于一直线河岸的岸边A处,乙村与甲村在河的同侧,乙村位于离河岸40km的B处,乙村到河岸的垂足D与A相距50km,两村要在此岸边合建一个自来水厂C,从自来水厂到甲村和乙村的水管费用分别为每千米
如图,有甲乙两个村庄,甲村位于一直线河岸的岸边A处,乙村与甲村在河的同侧,乙村位于离河岸40km的B处,乙村到河岸的垂足D与A相距50km,两村要在此岸边合建一个自来水厂C,从自来水厂到甲村和乙村的水管费用分别为每千米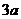 元和
元和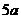 元. 现要进行工程费用测算.
元. 现要进行工程费用测算.
(Ⅰ)求出水管总费用关于水厂C到D的距离的函数关系式;
(Ⅱ)问自来水厂C建在何处,才能使水管总费用最省?
(21)(本小题満分12分)
在以O为原点的直角坐标系中,点A(3,-1)为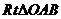 的直角顶点. 已知|AB|=2|OA|,且点B的纵坐标大于零.
的直角顶点. 已知|AB|=2|OA|,且点B的纵坐标大于零.
(Ⅰ)求向量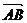 的坐标;
的坐标;
(Ⅱ)是否存在实数a,使二次函数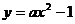 的图像上总有关于直线OB对称的两个不同的点?若不存在,说明理由;若存在,求a的取值范围.
的图像上总有关于直线OB对称的两个不同的点?若不存在,说明理由;若存在,求a的取值范围.
(22)(本小题満分14分)
已知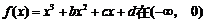 上是增函数,在[0,2]上是减函数,且方程
上是增函数,在[0,2]上是减函数,且方程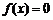 有三个根,它们分别为
有三个根,它们分别为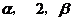 .
.
(Ⅰ)求c的值;
(Ⅱ)求证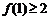 ;
;
(Ⅲ)求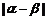 的取值范围.
的取值范围.
(13)平面内一动点P到直线2x+3y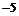 =0和到点M(1,1)的距离相等,则P点的轨迹为______________
(写出轨迹名称).
=0和到点M(1,1)的距离相等,则P点的轨迹为______________
(写出轨迹名称).
(14)函数y=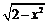 (
(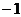 ≤x≤0)的反函数为_______________.
≤x≤0)的反函数为_______________.
(15)若甲以10发8中,乙以10发6中,丙以10发7中的命中率打靶,三人各射击一次,则三人中只有一人命中的概率是___________.
(16)一个三位数abc称为“凹数”,如果该三位数同时满足a>b且b<c,那么所有不同的三位“凹数”的个数是_____________________.
(1)设集合A = {x|x2-1>0}, B= {x|log2x>0}, 则A∩B等于
(A){x|x>1} (B) {x|x>0} (C){x|x<-1} (D) {x|x<-1或x>1}
(2)若(x2-1)+(x2-2x-3)i是纯虚数,则实数x的值是
(A)1 B) -1 (C) ±1 (D) 以上都不对
(3)已知等差数列{an}的各项均为正,且公差不为0,设P=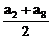 ,Q=
,Q=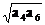 ,则P与Q的大小关系为
,则P与Q的大小关系为
(A) P>Q (B) P<Q (C) P=Q (D) 无法确定
(4)已知sin(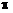 +
+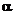 )=
)=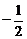 且tan
且tan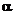 <0则cos
<0则cos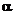 的值为
的值为
(A) 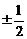 (B)
(B)
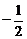 (C)
(C) 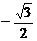 (D)
(D) 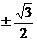
(5)直线l1,l2互相平行的一个充分条件是
(A) l1,l2都平行于平面 (B)
l1,l2与平面
(B)
l1,l2与平面 所成的角相等
所成的角相等
(C) l1平行于l2所在平面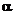 (D) l1,l2都垂直于平面
(D) l1,l2都垂直于平面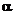
(6)平面上有四个互异的点A、B、C、D,满足(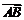 -
-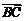 )·(
)·(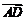 -
-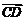 )=0,则三角形ABC是
)=0,则三角形ABC是
(A) 直角三角形 (B) 等腰三角形
(C) 等腰直角三角形 (D) 等边三角形
(7)将一张坐标纸折叠一次,使点(10,0)与(-6,8)重合,则与点(-4,2)重合的点是
(A) (4,-2) (B) (4,-3) (C) (3, 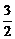 ) (D) (3,-1)
) (D) (3,-1)
(8)对一组数据Zi(i=1,2,3,…,n),如果将它们改变为Zi-C(i=1,2,3,…,n),其中C≠0,则下面结论正确的是
(A) 平均数与方差均不变 (B) 平均数变了,而方差保持不变
(C) 平均数不变,方差变了 (D) 平均数与方差均发生了变化
(9)正方体的八个顶点中有四个恰为正四面体的顶点,则正方体的全面积与正四面体的全面积之比为
(A) 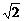 (B)
(B) 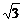 (C)
(C)
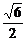 (D)
(D)
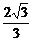
(10)F1、F2是双曲线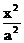
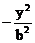 =1的左、右两个焦点,P是双曲线右支上任一点,从右焦点向∠F1PF2的平分线作垂线,垂足为M,点M的轨迹是曲线C的一部分,则曲线C是
=1的左、右两个焦点,P是双曲线右支上任一点,从右焦点向∠F1PF2的平分线作垂线,垂足为M,点M的轨迹是曲线C的一部分,则曲线C是
(A) 圆 (B) 椭圆 (C) 双曲线 (D) 抛物线
(11)已知函数f(x)=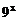
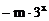 +m+1对x∈(0,
+m+1对x∈(0,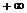 )的图象恒在x轴上方,则m的取值范围是
)的图象恒在x轴上方,则m的取值范围是
(A) 2-2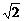 <m<2+2
<m<2+2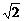 (B) m<2
(B) m<2
(C) m<2+2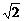 (D) m≥2+2
(D) m≥2+2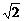
(12)a1、b1、c1、a2、b2、c2均为非零实数,不等式a1x2+b1x+c1>0和a2x2+b2x+c2>0的解集分别为集合M和N,那么“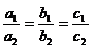 ”是“M=N”的
”是“M=N”的
(A)充分非必要条件. (B)必要非充分条件.
(C)充要条件 (D)既非充分又非必要条件.
(17)(本小题满分8分)
设平面上有两个向量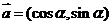
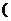 00≤α<3600
00≤α<3600 ,
,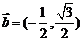
(Ⅰ)证明:(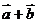 )⊥(
)⊥(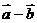 );
);
(Ⅱ)若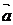 ∥
∥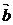 ,求角
,求角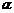 。
。
(18)(本小题满分10分)
已知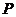 是正方形
是正方形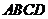 平面外一点,
平面外一点,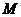 、
、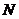 分别是
分别是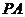 、
、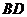 上的点,且
上的点,且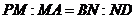
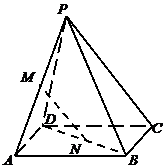
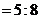 .求证:直线
.求证:直线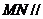 平面
平面
(19)(本小题满分10分)
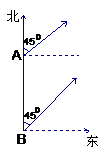 甲船由A岛出发向北偏东450的方向作匀速直线航行,速度为15
甲船由A岛出发向北偏东450的方向作匀速直线航行,速度为15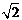 海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东450的方向作匀速直线航行,速度为20
海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东450的方向作匀速直线航行,速度为20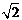 海里/小时(如图)。求两船出发后多长时间相距最近?最近距离为多少海里?
海里/小时(如图)。求两船出发后多长时间相距最近?最近距离为多少海里?
(20)(本小题满分12分)
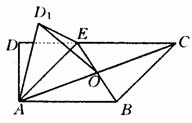 如图,在梯形ABCD中,AB∥CD,∠ADC=90°,3AD=DC=3,AB=2,E是DC上一点,满足DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=60°,设AC与BE的交点O.
如图,在梯形ABCD中,AB∥CD,∠ADC=90°,3AD=DC=3,AB=2,E是DC上一点,满足DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=60°,设AC与BE的交点O.
(Ⅰ)试用基向量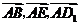 表示向量
表示向量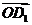 ;
;
(Ⅱ)求异面直线OD1与AE所成的角;
(Ⅲ)判断平面D1AE与平面ABCE是否垂直?并说明理由.
(13)已知|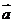 |=1,|
|=1,|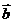 |=2,|
|=2,|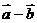 |=2,则|
|=2,则|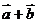 |= .
|= .
(14)把函数f(x)的图象按向量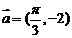 平移后得到函数
平移后得到函数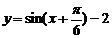 的图象, 则f(x)=
.
的图象, 则f(x)=
.
(15)已知RtΔABC,∠ACB=90°,点P是ΔABC所在平面α外的一点,若PA=PB=PC,则平面PAB与平面α的位置关系是 .
(16)若Rt△ABC在给定平面α上的射影有如下判断:
①可能是一条线段;②可能是直角三角形;③可能是锐角三角形;④可能是钝角三角形;⑤可能是一条直线。
其中正确判断的序号是 (把你认为正确的判断的序号都填上)。
(1)在平面四边形ABCD中,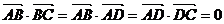 ,则该四边形是
,则该四边形是
(A)平行四边形 (B)矩形 (C)菱形 (D)正方形
(2)三个平面两两相交有三条交线,则这三条交线的位置关系
(A)互相平行 (B)相交于一点
(C)互相平行或交于一点 (D)与以上不同的答案
(3)已知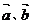 是两个非零向量,则
是两个非零向量,则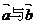 不共线是
不共线是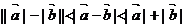 的
的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)不充分不必要条件
(4)已知异面直线a、b分别在平面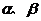 内,且
内,且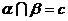 那么直线c
那么直线c
(A)与a、b都相交 (B)与a、b都不相交
(C)只与a、b中的一条相交 (D)至少与a、b中的一条相交
(5)已知a、b为两条不同的直线,α、β为两个不同的平面,且a⊥α,b⊥β,则下列命题中的假命题是
(A)若a∥b,则α∥β (B)若α⊥β,则a⊥b
(C)若a、b相交,则α、β相交 (D)若α、β相交,则a、b相交
(6)下列命题是真命题的是
(A)分别表示空间向量的有向线段所在的直线是异面直线,则这两个向量不是共面向量
(B)若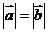 ,则
,则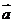 ,
,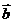 的长度相等而方向相同或相反
的长度相等而方向相同或相反
(C)若向量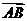 ,
,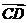 满足
满足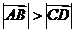 ,且
,且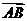 与
与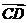 同向,则
同向,则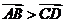
(D)若两个非零向量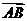 与
与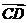 满足
满足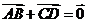 ,则
,则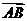 //
//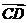
(7)A、B、C是不共线的三点,O是空间任意一点,若点P满足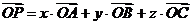 ,则当实数
,则当实数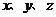 满足下列那个条件时,P、A、B、C四点共面.
满足下列那个条件时,P、A、B、C四点共面.
(A)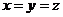 (B)
(B)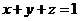 (C)
(C)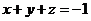 (D)
(D)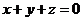
(8)已知一个简单多面体的各个顶点处都有三条棱,则顶点数V与面数F满足的关系式是
 (A)2F+V=4;
(B)2F-V=4;
(A)2F+V=4;
(B)2F-V=4;
(C)2F+V=2; (D)2F-V=2;
(9)如图,四棱锥P-ABCD的底面ABCD是一个正方形,PD垂直
于底面ABCD,则这个四棱锥的五个面中,互相垂直的平面共有
(A)3对 (B)4对
(C)5对 (D)6对
(10)若O为△ABC所在平面内一点,且满足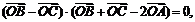 则一定有
则一定有
(A)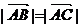 (B)
(B)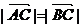
(C)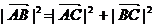 (D)
(D)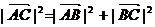
(11)设m,n是两条不同的直线,α、β、γ是三个不同的平面。给出下列四个命题:
①若m⊥α,n∥α,则m⊥n; ②若α∥β,β∥γ,m⊥α,,则m⊥γ;
③若m∥α,n∥α,则m∥n; ④若α⊥γ,β⊥γ,则α∥β。
其中正确命题的序号是:(A)①和② (B)②和③ (C)③和④ (D)①和④
(12)从正方体的八个顶点中任取三个点为顶点作三角形,其中直角三角形的个数为
(A)40 (B)48 (C)52 (D)56
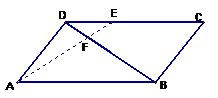
(17)(本小题满分8分)
平行四边形ABCD中,已知: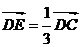 ,
,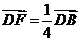 , 求证:A、E、F三点共线。
, 求证:A、E、F三点共线。
(18)(本小题满分10分)
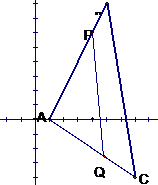
已知△ABC的顶点坐标为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在边AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分.
(19)(本小题满分10分)在正方体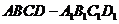 中,E、F、G、H为
中,E、F、G、H为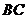 、
、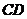 、
、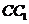 、
、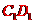 中点.
中点.
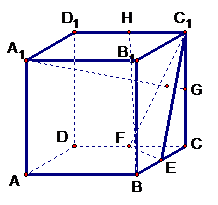 (Ⅰ)求证:
(Ⅰ)求证: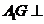 平面
平面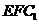 ;
;
(Ⅱ)求证: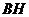 //平面
//平面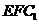 。
。
(20)(本小题满分12分)
已知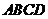 为直角梯形,
为直角梯形,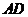 //
//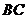 ,
,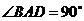 ,
,  ,
, 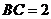 ,
, 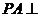 平面
平面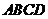 ,
,
(Ⅰ)若异面直线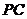 与
与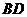 所成的角为
所成的角为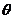 ,且
,且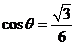 ,求
,求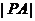 ;
;
(Ⅱ)在(Ⅰ)的条件下,设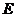 为
为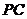 的中点,能否在
的中点,能否在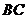 上找到一点
上找到一点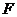 ,使
,使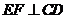 ?
?
(Ⅲ)在(Ⅱ)的条件下,求二面角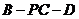 的大小.
的大小.
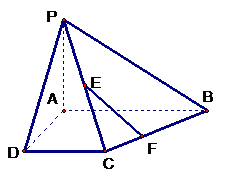
(13) 是球
是球 面上的四个点,
面上的四个点, 两两垂直,且
两两垂直,且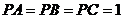 ,则球的体积为__________.
,则球的体积为__________.
(14)设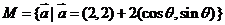 ,
,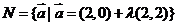 ,则
,则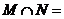
(15)已知: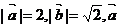 与
与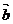 的夹角为45°,要使
的夹角为45°,要使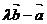 与
与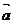 垂直,则
垂直,则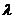 =
.
=
.
(16)向量的命题:①若非零向量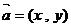 ,向量
,向量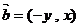 ,则
,则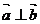 ;②四边形ABCD是菱形的充要条件是
;②四边形ABCD是菱形的充要条件是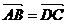 且
且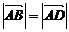 ;③若点G是
;③若点G是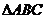 的重心,则
的重心,则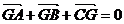 ④
④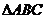 中,
中,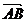 和
和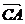 的夹角为
的夹角为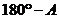 ,其中正确的命题序号是
__________.
,其中正确的命题序号是
__________.
(1)已知向量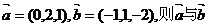 的夹角为
的夹角为
(A)0° (B)45°
(C)90° (D)180°
(2)在空间四边形ABCD中,AB=BC,AD=DC,则对角线AC与BD所成角的大小是
(A)90° (B)60° (C)45° (D)30°
(3)将函数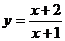 的图象按向量
的图象按向量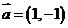 平移后所得图象的函数解析式为
平移后所得图象的函数解析式为
(A)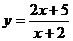 (B)
(B)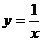 (C)
(C)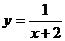 (D)
(D)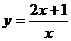
(4)已知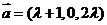 ,
,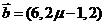 ,若
,若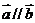 ,则
,则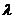 与
与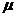 的值分别为
的值分别为
(A)-5,-2 (B)5,2
(C)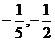 (D)
(D)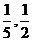
(5)若向量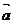 、
、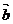 的坐标满足
的坐标满足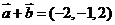 ,
,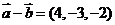 ,则
,则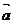 ·
·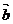 等于
等于
(A)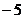 (B)
(B)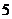 (C)
(C)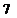 (D)
(D)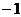
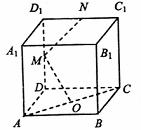 (6)在正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,M、N分别
(6)在正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,M、N分别
是棱DD1、D1C1的中点,则直线OM
(A)是AC和MN的公垂线
(B)垂直于AC,但不垂直于MN
(C)垂直于MN,但不垂直于AC
(D)与AC、MN都不垂直
(7)地球表面上从A地(北纬45°,东经120°)到B地(北纬45°,东经30°)的球面距离为(地球半径为R)
(A)R (B)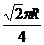 (C)
(C)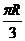 (D)
(D)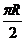
(8)如图,在一根长11cm,外圆周长6cm的圆柱形柱体外表面,用一根细铁丝缠绕,组成10个螺旋,如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为
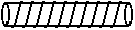 (A)61cm
(B)
(A)61cm
(B)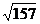 cm
cm
(C)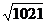 cm (D)
cm (D)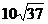 cm
cm
(9)在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是 ( )
(A)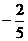 (B)
(B)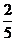 (C)
(C)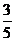 (D)
(D)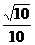
(10)平面内有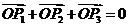 且
且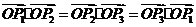 ,则
,则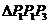 一定是
一定是
(A)钝角三角形 (B)直角三角形
(C)等腰三角形 (D)等边三角形
(11)在棱长为2的正方体AC1中,点E,F分别是棱AB,BC的中点,则点C1到平面B1EF的距离是
(A)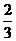 (B)
(B)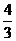 (C)
(C)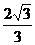 (D)
(D)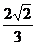
(12)设PA,PB,PC是从点P引出的三条射线,每两条的夹角都等于60°,则直线PC与平面APB所成角的余弦值是
(A)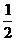 (B)
(B)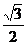 (C)
(C)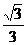 (D)
(D)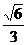
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com