
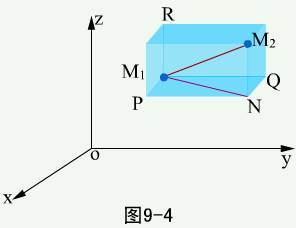
设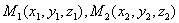 ,则两点间距离为
,则两点间距离为
第二节 矢量的概念及其运算
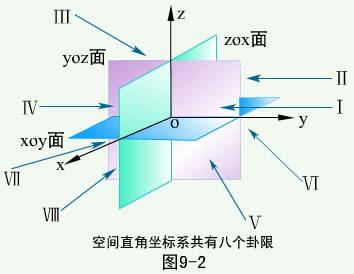
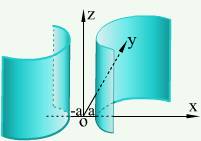
由三条相互垂直相交的数轴x轴(横轴)、y轴(纵轴)、z轴(竖轴)按右手法则构成的坐标系称为空间直角坐标系,三个数轴的公共交点O为坐标原点。
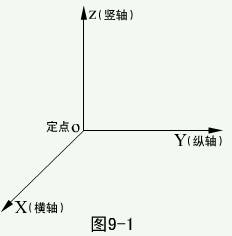
其中任两个数轴确定一个平面,称为坐标面,三个坐标面:XOY面,XOZ面,YOZ面。三个坐标面将空间分成了八个部分,称为八个卦限,记为:Ⅰ-Ⅷ。(见图)
空间中的点P与坐标 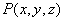 一一对应,特殊点的坐标的特点:坐标面上的点,坐标轴上的点。(见图)
一一对应,特殊点的坐标的特点:坐标面上的点,坐标轴上的点。(见图)
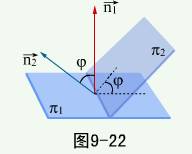
两平面的夹角:指它们的法矢量间的夹角 (取锐角)
(取锐角)
设 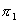 :
: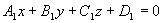
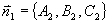
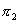 :
: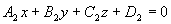
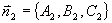
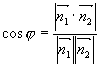
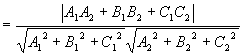
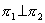 的充要条件:
的充要条件: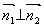 ,即
,即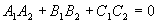
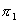 ∥
∥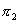 的充要条件:
的充要条件: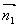 ∥
∥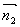 ,即
,即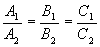
例9 研究下列各组平面的位置关系
(1)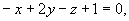 与
与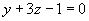 ;
;
(2)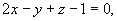 与
与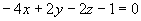 ;
;
(3)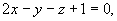 与
与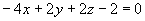 。
。
解 (1)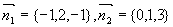
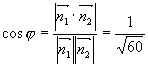 ,所以相交,夹角
,所以相交,夹角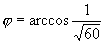
(2)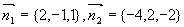
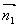 ∥
∥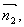 平行,但不重合。(因为点
平行,但不重合。(因为点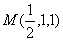 在第一个平面上,但不在第二个平面上)。
在第一个平面上,但不在第二个平面上)。
(3)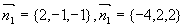
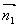 ∥
∥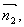 平行,且重合。
平行,且重合。
例10 设有两平面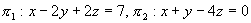 ,求这两平面的夹角。
,求这两平面的夹角。
解 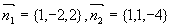
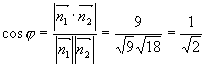
所以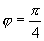
例11 设有两平面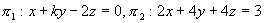 ,如果两平面垂直,则
,如果两平面垂直,则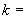 ?
?
解 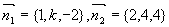
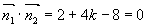 ,
,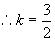
 两直线的夹角:指它们的方向矢量间的夹角
两直线的夹角:指它们的方向矢量间的夹角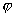 (取锐角)
(取锐角)
设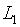 :
: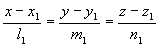
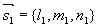
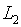 :
: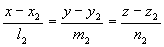
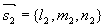
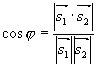
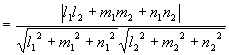
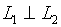 充要条件:
充要条件: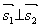 ,即
,即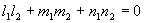
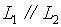 充要条件:
充要条件: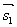 ∥
∥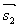 ,即
,即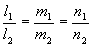
例12 求两条直线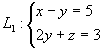 与
与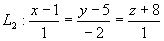 的夹角。
的夹角。
解 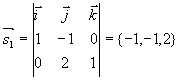 ,
,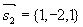
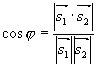
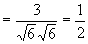
所以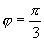
 平面与直线的夹角:指直线与它在平面上的投影直线间的夹角
平面与直线的夹角:指直线与它在平面上的投影直线间的夹角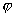 (取锐角)
(取锐角)

设平面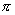 :
: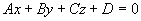
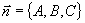
直线L: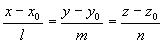
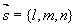
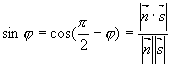
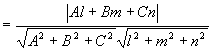
 的充要条件:
的充要条件: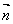 ∥
∥ ,即
,即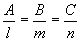
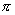 ∥
∥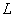 的充要条件:
的充要条件: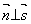 ,即
,即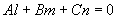
例13 求直线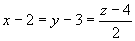 与平面
与平面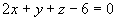 的交点和夹角。
的交点和夹角。
解 直线的参数方程为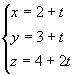
代入平面方程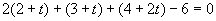
解得 t=-1 ,代入直线的参数方程中得交点(1,2,2)
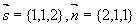
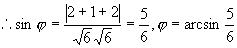
例14 求过平面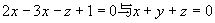 的交线,且与第二个平面垂直的平面方程。
的交线,且与第二个平面垂直的平面方程。
解 法一:设所求平面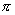 的法线矢量为
的法线矢量为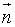 ,由题意
,由题意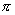 过直线
过直线
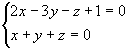
将其化为对称式
令z=2,解得直线过点(-1,-1,2)
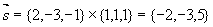
 直线对称式方程为
直线对称式方程为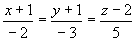
又因为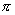 的法线垂直于
的法线垂直于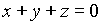 的法矢量且垂直于
的法矢量且垂直于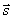
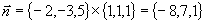
点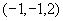 在所求平面
在所求平面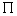 上,由点法式得
上,由点法式得
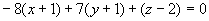
即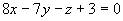
法二:设所求平面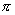 的方程为
的方程为
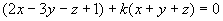
即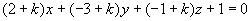
注:这是过两平面交线的平面束方程。
又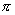 垂直于平面
垂直于平面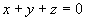 ,由两平面垂直的充要条件
,由两平面垂直的充要条件
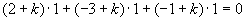
解出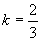 ,代入上面方程得
,代入上面方程得
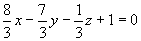
即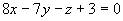
例15 求过直线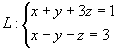 且与平面
且与平面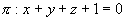 垂直的平面方程。
垂直的平面方程。
解 设所求平面方程为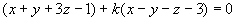
即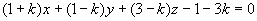
因所求平面方程与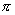 垂直,所以
垂直,所以
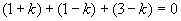
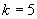
所求平面方程为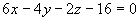
即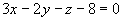
例16 求过点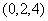 且与平面
且与平面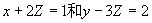 都平行的直线方程。
都平行的直线方程。
解 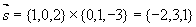
所求直线为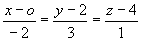
例17 求过点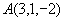 及直线
及直线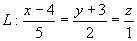 的平面方程。
的平面方程。
解 点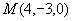 在所求平面上,作
在所求平面上,作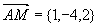
直线的方向矢量 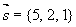
所求平面方程法矢量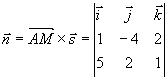
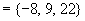
所求平面方程为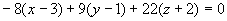
即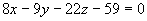 。
。
例18 求过两条直线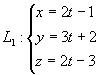 与
与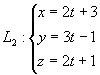 的平面方程。
的平面方程。
解 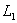 上的点
上的点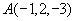 ,
,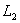 上的点
上的点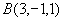 均在所求平面上,
均在所求平面上,
作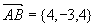 所求平面法矢量为
所求平面法矢量为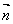 ,有
,有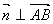 且
且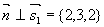
可取
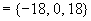
所求平面方程为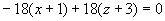
即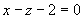
平行于某直线L的非零矢量称为该直线的方向矢量,记为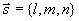
对称式方程:已知直线L过点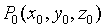 且方向矢量
且方向矢量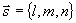 ,求此直线方程。
,求此直线方程。
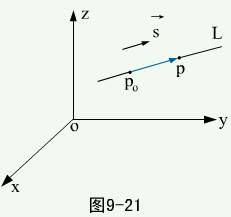
在直线上任取一点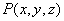 ,作矢量
,作矢量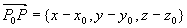 则
则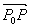 ∥
∥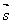 ,所以有
,所以有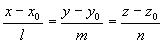 ,此称为直线的对称式方程。
,此称为直线的对称式方程。
注:当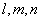 中有零时,直线仍可写成对称式形式如
中有零时,直线仍可写成对称式形式如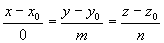 应理解为两个平面的交线,即
应理解为两个平面的交线,即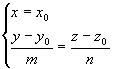 。
。
参数式方程: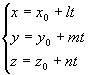 其中
其中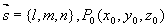 为直线上一点。
为直线上一点。
一般式方程: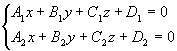
其中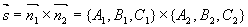
例7 求平行于直线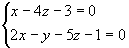 且过点
且过点 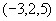 的直线方程。
的直线方程。
解 所求直线方向矢量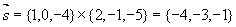 所求直线方程为
所求直线方程为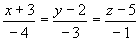
例8 化直线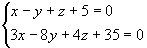 为对称式方程。
为对称式方程。
解 令z=-5,解方程组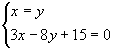 得
得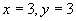 ,点
,点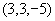 在直线上。
在直线上。
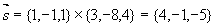
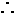 对称式方程为
对称式方程为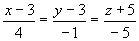
垂直于某平面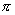 的非零矢量称为该平面的法线矢量,记作
的非零矢量称为该平面的法线矢量,记作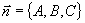 。
。
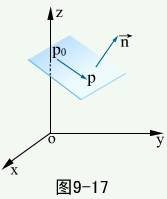
点法式方程:已知平面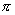 过点
过点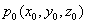 ,且与非零矢量
,且与非零矢量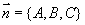 垂直(法矢量),求平面方程。
垂直(法矢量),求平面方程。
在平面上任取一点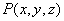 ,作矢量
,作矢量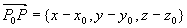 ,则
,则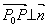 ,所以有
,所以有
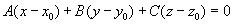
此称为平面的点法式方程。
一般式方程: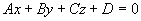
其中:法矢量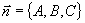 ,
,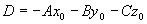
截矩式方程: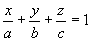
注:三元一次方程表示一个平面。
特殊位置的平面方程:
(1)过原点 ( )
)
(2)平行于坐标轴
平行于x轴( )
)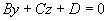 过X轴(
过X轴(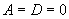 )
)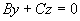
平行于y轴(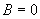 )
)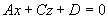 过Y轴(
过Y轴(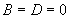 )
)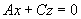
平行于z轴(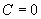 )
)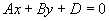 过Z轴(
过Z轴(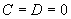 )
)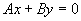
(3)垂直于坐标轴
垂直于x轴(平行于YOZ坐标面)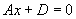
垂直于y轴(平行于XOZ坐标面)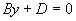
垂直于z轴(平行于XOY坐标面)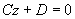
例1 求过点(6,2,-2)且与平面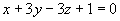 平行的平面方程。
平行的平面方程。
解 所求平面方程法矢量为
由点法式得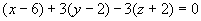
即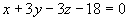
例2 求过三点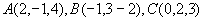 的平面方程。
的平面方程。
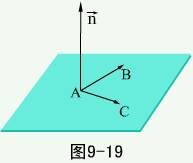
解 作矢量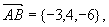
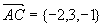
取法矢量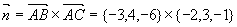
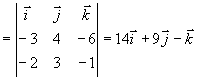
由点法式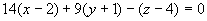
即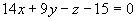 。
。
此题也可用下面的方法求解:
设平面方程为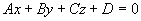
因平面过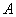 、
、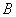 、
、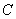 三点,将三点的坐标代入方程,得
三点,将三点的坐标代入方程,得
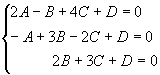
解出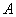 、
、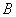 、
、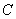 、
、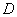 即可。
即可。
例3 求过三点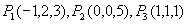 的平面方程。
的平面方程。
例4 过点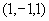 作垂直于两平面
作垂直于两平面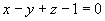 和
和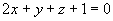 的平面,求此平面方程。
的平面,求此平面方程。
解 设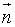 为所求平面法向量
为所求平面法向量
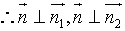 可取
可取
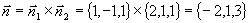
由点法式得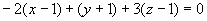
即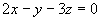
例5 求过点(1,-2,1)且与平面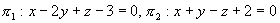 都垂直的平面方程。
都垂直的平面方程。
例6 求平面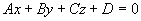 外一点
外一点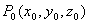 到该平面的距离
到该平面的距离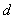 。
。
解 在平面上任取一点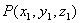 ,作矢量
,作矢量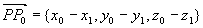
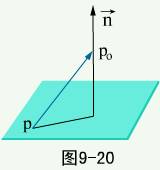
则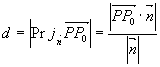
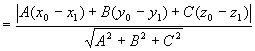
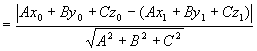
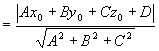
如:点(1,-1,2)到平面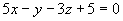 的距离为
的距离为
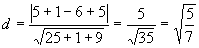
一条平面曲线c,绕着同一平面内的一条直线L旋转一周,这时由c所产生的曲面称为旋转面,c称为旋转面的母线,L为旋转面的轴。
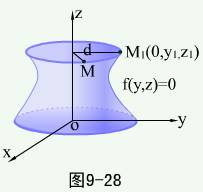
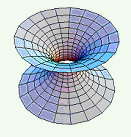
YOZ平面内曲线 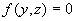 ,绕Z轴旋转所得旋转面方程为
,绕Z轴旋转所得旋转面方程为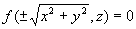 ,绕Y轴旋转所得旋转面方程为
,绕Y轴旋转所得旋转面方程为 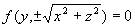 。
。
XOZ平面内曲线 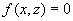 绕Z轴旋转所得旋转面方程为
绕Z轴旋转所得旋转面方程为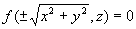 ,绕X轴旋转所得旋转面方程为
,绕X轴旋转所得旋转面方程为 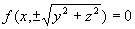 。
。
XOY平面内曲线 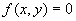 绕X轴旋转所得旋转面为
绕X轴旋转所得旋转面为 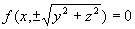 ,绕Y轴旋转所得曲面为
,绕Y轴旋转所得曲面为 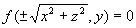 。
。
例4 由抛物线 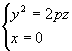 绕Z轴旋转产生的旋转面方程为
绕Z轴旋转产生的旋转面方程为 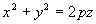 (旋转抛物面)。
(旋转抛物面)。
例5 由椭圆 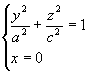 绕Z轴、Y轴旋转,求旋转面方程。
绕Z轴、Y轴旋转,求旋转面方程。
解 绕Z轴旋转 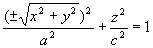 既
既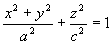 (旋转椭球面)
绕Y轴旋转
(旋转椭球面)
绕Y轴旋转 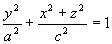 (旋转椭球面)。
(旋转椭球面)。
先分析一个例子
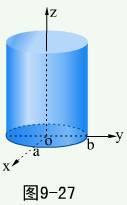
例3 方程 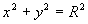 表示怎样的曲面?
表示怎样的曲面?
解 方程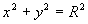 在
在 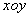 面上表示圆心在原点、
面上表示圆心在原点、
半径为 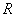 的圆。
的圆。
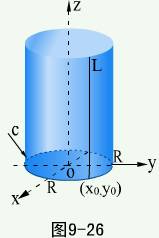
在空间直角坐标系中,这方程不含z,即不论空间点的竖坐标 怎样,只要它的横坐标
怎样,只要它的横坐标  和纵坐标
和纵坐标 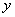 能满足这方程,那么这些点就在这曲面上。即凡是通过
能满足这方程,那么这些点就在这曲面上。即凡是通过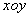 面内圆
面内圆 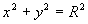 上一点
上一点 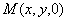 ,且平行于
,且平行于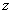 轴的直线
轴的直线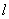 都在这曲面上,因此,这曲面可以看作是由平行于
都在这曲面上,因此,这曲面可以看作是由平行于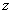 轴的直线
轴的直线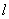 沿
沿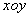 面上的圆
面上的圆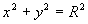 移动而形成的。这曲面叫圆柱面,
移动而形成的。这曲面叫圆柱面,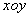 面上的圆
面上的圆 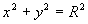 叫做它的准线,平行于
叫做它的准线,平行于 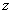 轴的直线
轴的直线 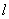 叫做它的母线。
叫做它的母线。
一般地,沿定曲线c并平行于定直线Z移动的动直线 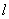 所形成的轨迹叫柱面,定曲线c叫准线,动直线
所形成的轨迹叫柱面,定曲线c叫准线,动直线 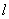 叫柱面的母线。
叫柱面的母线。
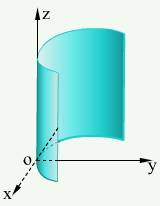
 不含
不含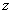 的方程
的方程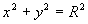 表示母线平行于
表示母线平行于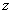 轴的圆柱面。类似地,方程
轴的圆柱面。类似地,方程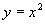 表示母线平行于
表示母线平行于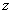 轴的抛物柱面。方程
轴的抛物柱面。方程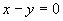 表示母线平行于
表示母线平行于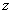 轴的平面,
轴的平面,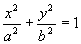 表示母线平行于
表示母线平行于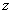 轴的椭圆柱面,
轴的椭圆柱面,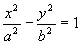 表示母线平行于
表示母线平行于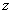 轴的双曲柱面。
轴的双曲柱面。
一般地,只含  、
、  而缺
而缺 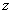 的方程
的方程 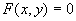 ,在空间直角坐标系中表示母线平行于
,在空间直角坐标系中表示母线平行于 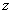 轴柱面,其准线是
轴柱面,其准线是 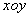 面上的曲线c:
面上的曲线c: 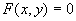 。
。
由类似的分析方法可知:
母线平行于 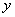 轴的柱面方程为
轴的柱面方程为 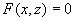
母线平行于 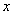 轴的柱面方程为
轴的柱面方程为 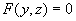
像在平面解析几何中把平面曲线当作动点的轨迹一样,在空间解析几何中,任何曲面都看作动点的几何轨迹。这样,在空间直角坐标系中,根据动点的运动规律可建立起关于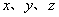 的方程
的方程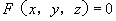 。
。
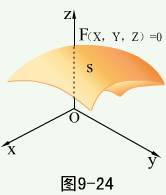
定义:如果曲面S与一个三元方程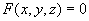 存在关系
存在关系
(1)曲面上任何点的坐标都满足方程,
(2)凡是坐标满足方程的点都在曲面上,
那么方程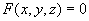 称为曲面S的方程,曲面S称为方程
称为曲面S的方程,曲面S称为方程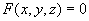 的图形。
的图形。
研究空间曲面时有两方面的问题:(1)已知一曲面作为动点的几何轨迹,建立曲面的方程,(2)已知方程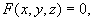 研究它所表示的曲面的形状。
研究它所表示的曲面的形状。
作为问题(1),我们建立球面方程和旋转曲面的方程,作为问题(2)我们讨论柱面。
例1 到定点的距离等于定长的点的几何轨迹是球面,定点是球心,定长是半径。建立球心在点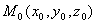 ,半径为
,半径为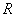 的球面方程。
的球面方程。
解: 设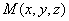 是球面上的任一点, 则
是球面上的任一点, 则 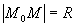
即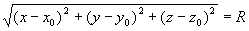
所以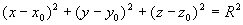
球心在原点,半径为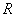 的球面方程为
的球面方程为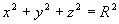 。
。

例2 讨论方程 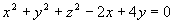 表示怎样的曲面?
表示怎样的曲面?
解 通过配方,原方程可写为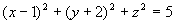
所以,此方程表示球心在点 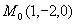 ,半径为
,半径为 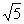 的球面。
的球面。
通过空间曲线 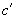 作母线平行于z轴(x轴,y轴)的柱面,这柱面称为
作母线平行于z轴(x轴,y轴)的柱面,这柱面称为 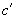 在xoy(yoz,zox)坐标面上的投影柱面,投影柱面与xoy坐标面的交线c称为
在xoy(yoz,zox)坐标面上的投影柱面,投影柱面与xoy坐标面的交线c称为 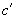 在xoy坐标面上的投影曲线。
在xoy坐标面上的投影曲线。
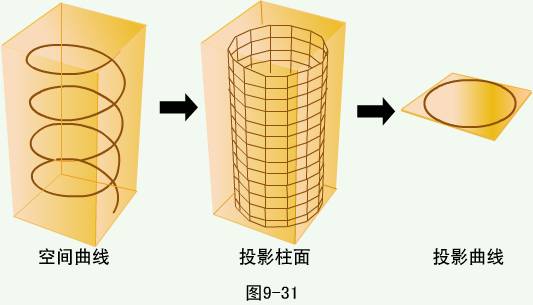
曲线 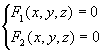 在xoy坐标面上的投影曲线方程为
在xoy坐标面上的投影曲线方程为 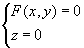 ,
, 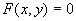 是由曲线方程消去变量z后得到的。
是由曲线方程消去变量z后得到的。
同样可得,在yoz坐标面上的投影曲线方程为 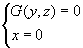 ,在zox坐标面上的投影曲线方程为
,在zox坐标面上的投影曲线方程为 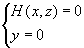 。
。
例3 求曲线 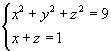 在坐标面上的投影曲线的方程。
在坐标面上的投影曲线的方程。
解 消去z,得到在xoy面上的投影曲线为 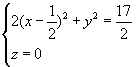 消去x,得到在yoz面上的投影曲线为
消去x,得到在yoz面上的投影曲线为 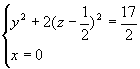 消去y,得到在xoz面上的投影曲线为
消去y,得到在xoz面上的投影曲线为
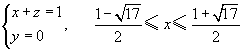 。
。
空间曲线除了可用一般式方程表示外,也可用参数方程来表示,在一般式方程中,令 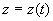 ,解出
,解出 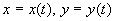 ,则可得到空间曲线的参数方程。
,则可得到空间曲线的参数方程。
空间曲线的参数方程为 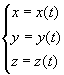 (随着t的变动可得到曲线C上的全部点)。
(随着t的变动可得到曲线C上的全部点)。
例2 将曲线的一般方程 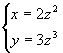 化为参数方程。
化为参数方程。
解 令 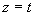 ,得曲线的参数方程为
,得曲线的参数方程为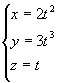
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com