
2. 函数和、差、积、商的微分法则
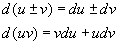
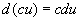 (C为常数)
(C为常数)
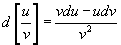
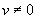
1. 由基本导数公式可得基本微分公式,书中168页的表要背下来。
3.设 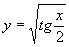 ,则
,则
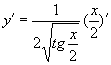
例16 设下列函数可导,求它们的导数
(1) 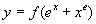 (2)
(2) 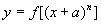
(3) 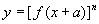
解 (1) 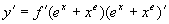
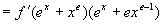
(2) 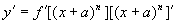
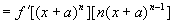
(3) 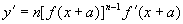
例17 设 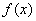 可导,且
可导,且
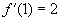 ,求
,求
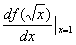
解 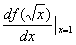
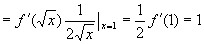
例18 已知 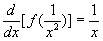 ,求
,求
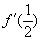
解 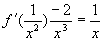 ,
, 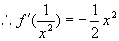 ,
,
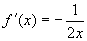 ,
,
所以 
例19 设 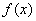 是可导的偶函数,证明:
是可导的偶函数,证明:
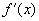 是奇函数。
是奇函数。
证明 :因 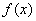 是偶函数,
是偶函数,
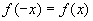
等号两边对 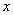 求导,
求导,
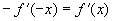 ,即
,即
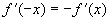
所以 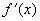 是奇函数。
是奇函数。
此结论也可用导数的定义证明。
2.设 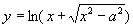 ,则
,则
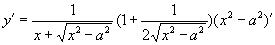
1.设 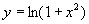 ,则
,则
(1) 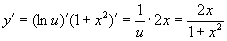
(2) 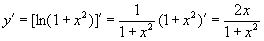
(3) 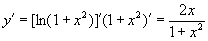
2. 当积分上限的函数是复合函数时,有
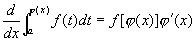
更一般的有 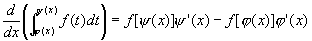
例1 (1)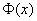
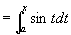 ,
则:
,
则: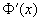 =
= 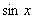
(2)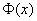
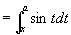
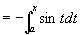 ,则:
,则: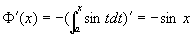
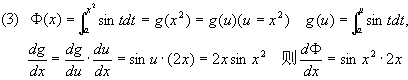
(4)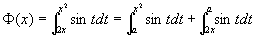 ,则:
,则:
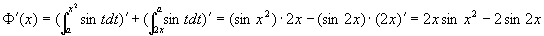
(5)设 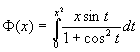 ,求:
,求: 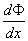
此题中 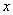 为函数的自变量,
为函数的自变量,
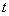 为定积分的积分变量,因而是两个函数乘积的形式
为定积分的积分变量,因而是两个函数乘积的形式
由求导法则
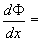
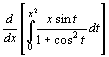 =
= 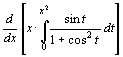
=
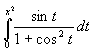 +
+ 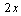
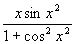
(6) 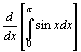 =0(因定积分的结果为一常数,故导数为零)
=0(因定积分的结果为一常数,故导数为零)
(7)设
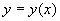 是方程
是方程
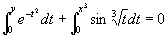 所确定的函数,求
所确定的函数,求
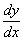
解 利用隐函数求导法则和变限积分求导法则有
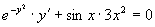 则
则 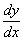 =
= 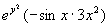
例2 设 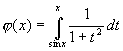 ,求
,求
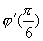 。
。
例3 设 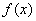 为连续函数,(1)若
为连续函数,(1)若 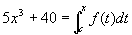 ,则
,则
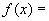 ______ ,
______ ,
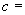 ___ 。 (2)
___ 。 (2)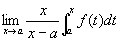
例4 求 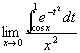
解 这是 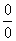 型不定式,用罗必塔法则
型不定式,用罗必塔法则
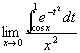
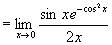
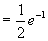

定理 (牛顿--莱公式)如果函数 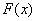 是连续函数
是连续函数
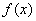 在区间
在区间
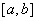
上的一个原函数,则
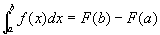
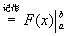
此公式表明:一个连续函数在区间 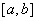 上的定积分等于它的任一个原函数在该区间上的增量,此公式也称为微积分基本公式。
上的定积分等于它的任一个原函数在该区间上的增量,此公式也称为微积分基本公式。
例5 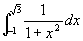
解 原式 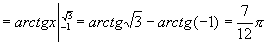
例6 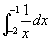
解 原式 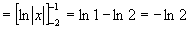
例7  求
求 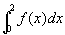
解 利用定积分的可加性分段积分,
 =
= 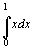 +
+ 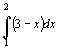 =2
=2
例8 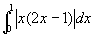
解 被积函数是分段函数,分段点 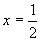 在积分区间
在积分区间
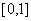 内,
内,
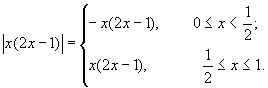
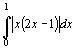 =
= 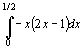 +
+ 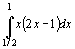 =1/4
=1/4
例9 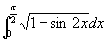
解 原式 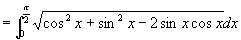
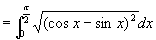
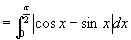
注意: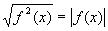 是分段函数
是分段函数
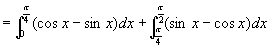
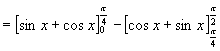
1. 由原函数的定义知, 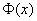 是连续函数
是连续函数
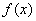 的一个原函数,因此,此公式
揭示了定积分与原函数之间的联系。
的一个原函数,因此,此公式
揭示了定积分与原函数之间的联系。
3. 规定 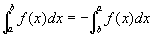
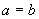 时 ,
时 , 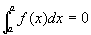

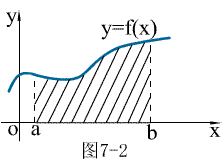
在 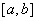 上
上
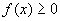 时,
时, 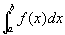 表示曲线
表示曲线
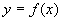 、两条直线
、两条直线
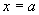 、
、
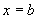 与
与
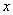 轴所围成的曲边梯形的面积;
轴所围成的曲边梯形的面积;
在 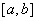 上
上
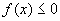 时,
时, 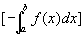 表示曲线
表示曲线
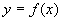 、两条直线
、两条直线
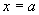 、
、
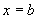 与
与
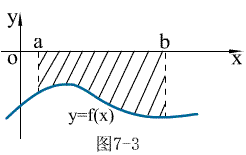
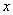 轴所围成的曲边梯形的面积(此时,曲边梯形在
轴所围成的曲边梯形的面积(此时,曲边梯形在
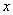 轴的下方);
轴的下方);
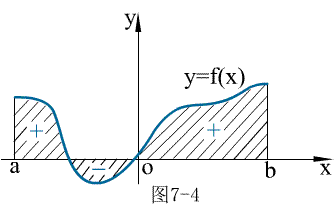
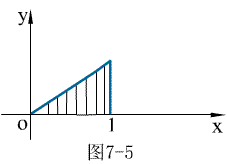
例1 利用定积分的几何意义写出下列积分值
(1) 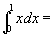
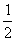 (三角形面积)
(2)
(三角形面积)
(2) 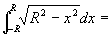
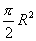 (半圆面积)
(半圆面积)


设 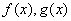 可积
可积
性质1 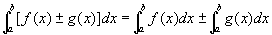
性质2 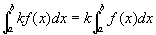
性质3 (定积分对区间的可加性) 对任何三个不同的数 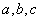 ,有
,有
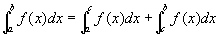
性质4 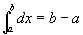
性质5 如果在区间 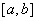 上,
上,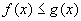 ,则
,则
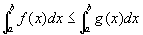
推论 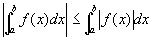
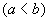
性质6 (定积分的估值) 设 M 及 m 分别是函数 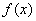 在区间
在区间
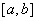 上的最大值及最小值,则
上的最大值及最小值,则
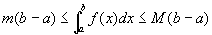
性质7 (定积分中值定理)
如果函数 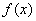 在区间
在区间
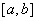 上连续,则在
上连续,则在
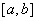 上至少有一点
上至少有一点
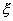 ,使
,使 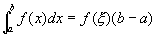
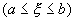 成立
成立
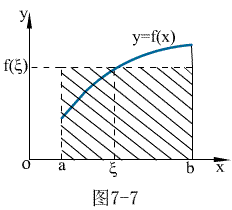
例2 比较下面两个积分的大小
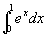 与
与 
解 设 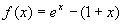 ,
,
在(0,1)内, 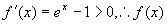 单调增
单调增
当 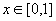 时,有
时,有
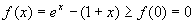 ,即
,即
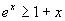
由性质5, 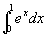


例3 估计积分 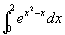 的值
的值
解 只需求出  在区间
在区间
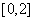 上的最大值、最小值即可。设
上的最大值、最小值即可。设
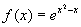 ,
,
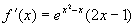 ,令
,令  ,得
,得 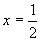 ,
,
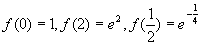
所以,在区间 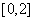 上
上 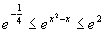
由性质6, 

设 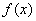 在区间
在区间
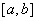 上连续,
上连续,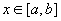 ,则定积分
,则定积分
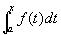 一定存在,
当
一定存在,
当 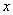 在
在
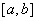 上变动时,它构成了一个
上变动时,它构成了一个
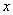 的函数,称为
的函数,称为
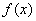 的变上限积分函数,
记作
的变上限积分函数,
记作 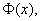 即
即
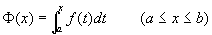

定理 如果函数 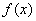 在区间
在区间
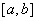 上连续,则积分上限的函数
上连续,则积分上限的函数
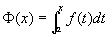 在
在
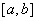 上具有导数,且导数是
上具有导数,且导数是
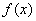 ,即
,即
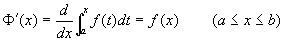
说明:
2. 由定义可知,定积分的值只与被积函数和积分区间有关,而与积分变量无关,所以
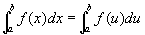
1. 如果(*)式右边极限存在,称 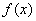 在区间
在区间
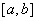 可积,下面两类函数在区间
可积,下面两类函数在区间
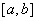 可积,(1)
可积,(1)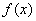 在区间
在区间 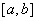 上连续,则
上连续,则
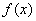 在
在
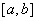 可积。(2)
可积。(2)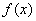 在区间
在区间 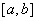 上有界且只有有限个间断点,则
上有界且只有有限个间断点,则
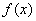 在
在
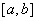 上可积。
上可积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com