
4.本课小结
(1)同角三角函数的三组关系式的前提是“同角”,因此 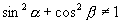 ,
,
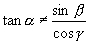 …….
…….
(2)诸如 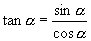 ,
,
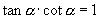 ,……它们都是条件等式,即它们成立的前提是表达式有意义.
,……它们都是条件等式,即它们成立的前提是表达式有意义.
(3)利用平方关系时,往往要开方,因此要先根据角所在象限确定符号,即要就角所在象限进行分类讨论.
课时作业:
3.演练反馈(投影)
(1)已知: 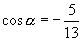 ,求
,求
 的其他各三角函数值.
的其他各三角函数值.
(2)已知 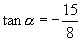 ,求
,求
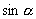 ,
,
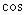 .
.
(3)化简: 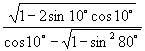
解答:(1)解:∵ 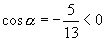 ,所以
,所以
 是第二、第三象限的角.
是第二、第三象限的角.
如果  是第二象限的角,则:
是第二象限的角,则:
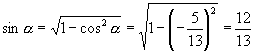
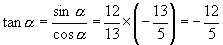
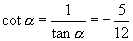
又 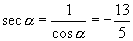
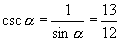
如果  是第三象限的角,那么
是第三象限的角,那么
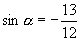
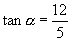
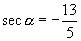
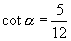
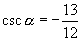
(2)解:∵ 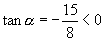 ∴
∴  是第二或第四象限的角
是第二或第四象限的角
由[例3]的求法可知当  是第二象限时
是第二象限时
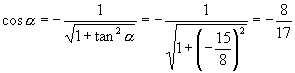
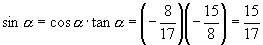
当  是第四象限时
是第四象限时
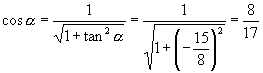
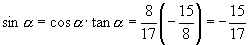
(3)解:原式 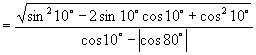
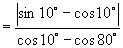
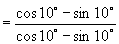
2.探索研究
 (1)复习任意角三角函数定义
(1)复习任意角三角函数定义
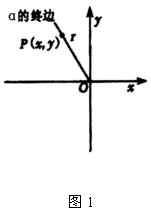
上节课我们已学习了任意角三角函数定义,如图1所示,任意角  的六个三角函数是如何定义的呢?
的六个三角函数是如何定义的呢?
在  的终边上任取一点
的终边上任取一点
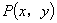 ,它与原点的距离是
,它与原点的距离是
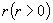 ,则角
,则角
 的六个三角函数的值是:
的六个三角函数的值是:
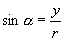 ;
; 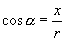 ;
; 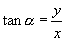
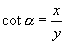 ;
; 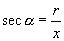 ;
; 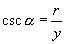
(2)推导同角三角函数关系式
观察 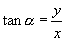 及
及
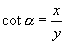 ,当
,当
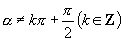 时,有何关系?
时,有何关系?
当 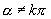 且
且
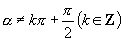 时
时
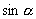 、
、
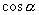 及
及
 有没有商数关系?
有没有商数关系?
通过计算发现  与
与
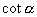 互为倒数:∵
互为倒数:∵
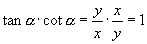 .
.
由于 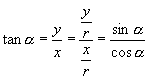 ,
,
这些三角函数中还存在平方关系,请计算
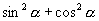 的值.
的值.
由三角函数定义我们可以看到:
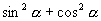
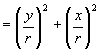
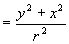
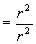
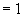 .
.
∴ 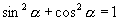 ,现在我们将同角三角函数的基本关系式总结如下:
,现在我们将同角三角函数的基本关系式总结如下:
①平方关系: 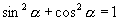
②商数关系: 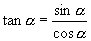
③倒数关系: 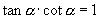
即同一个角  的正弦、余弦的平方和等于1,商等于角
的正弦、余弦的平方和等于1,商等于角  的正切,同一个角的正切、余切之积等于1(即同一个角的正切、余切互为倒数).上面这三个关系式,我们称之为恒等式,即当
的正切,同一个角的正切、余切之积等于1(即同一个角的正切、余切互为倒数).上面这三个关系式,我们称之为恒等式,即当  取使关系式两边都有意义的任意值时,关系式两边的值相等,在第二个式中,
取使关系式两边都有意义的任意值时,关系式两边的值相等,在第二个式中,
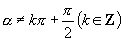 在第三个式中,
在第三个式中,
 的终边不在坐标轴上,这时式中两边都有意义,以后解题时,如果没有特别说明,一般都把关系式看成是意义的.其次,在利用同角三角函数的基本关系式时,要注意其前提“同角”的条件.
的终边不在坐标轴上,这时式中两边都有意义,以后解题时,如果没有特别说明,一般都把关系式看成是意义的.其次,在利用同角三角函数的基本关系式时,要注意其前提“同角”的条件.
(3)同角三角函数关系式的应用
同角三角函数关系式十分重要,应用广泛,其中一个重要应用是根据一个角的某一个三角函数,求出这个角的其他三角函数值.
[例1]已知 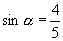 ,且
,且
 是第二象限角,求
是第二象限角,求
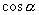 ,
,
 ,
,
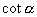 的值.
的值.
解:∵ 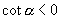 ,且
,且
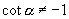 ,∴
,∴
 是第二或第三象限角.
是第二或第三象限角.
如果  是第二象限角,那么
是第二象限角,那么
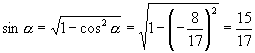
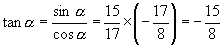
如果  是第三象限角,那么
是第三象限角,那么
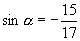 ,
,
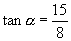
说明:本题没有具体指出
 是第几象限的角,则必须由
是第几象限的角,则必须由
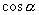 的函数值决定
的函数值决定
 可能是哪几象限的角,再分象限加以讨论.
可能是哪几象限的角,再分象限加以讨论.
[例2]已知 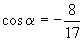 ,求
,求
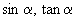 的值.
的值.
解: 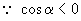 ,且
,且
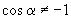 ,
,
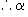 是第二或第三象限角.
是第二或第三象限角.
如果 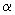 是第二象限角,那么
是第二象限角,那么
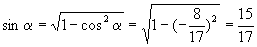
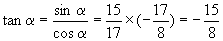
如果 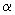 是第三象限角,那么
是第三象限角,那么
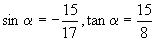 .
.
说明:本题没有具体指出
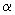 是第几象限角,则必须由
是第几象限角,则必须由
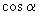 的函数值决定
的函数值决定
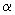 可能是哪几象限的角,再分象限加以讨论.
可能是哪几象限的角,再分象限加以讨论.
[例3]已知  为非零实数,用
为非零实数,用
 表示
表示
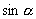 ,
,
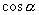 .
.
解:因为 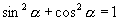 ,所以
,所以
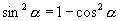
又因为 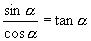 ,所以
,所以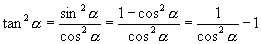
于是 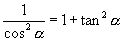 ∴
∴ 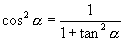
由  为非零实数,可知角
为非零实数,可知角
 的终边不在坐标轴上,考虑
的终边不在坐标轴上,考虑
 的符号分第一、第四象限及第二、三象限,从而:
的符号分第一、第四象限及第二、三象限,从而:
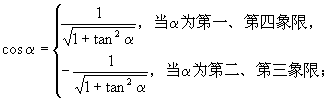
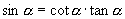

在三角求值过程中应尽量避免开方运算,在不可避免时,先计算与已知函数有平方关系的三角函数,这样可只进行一次开方运算,并可只进行一次符号说明.
同角三角函数关系式还经常用于化简三角函数式,请看例4
[例4]化简下列各式:
(1) 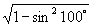 ;(2)
;(2) 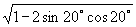 .
.
解:(1) 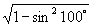 (2)
(2) 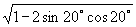
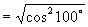
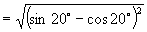
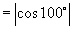
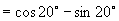
1.设置情境
与初中学习锐角三角函数一样,本节课我们来研究同角三角函数之间关系,弄清同角各不同三角函数之间的联系,实现不同函数值之间的互相转化.
2.会运用同角三角函数之间的关系求三角函数值或化简三角式.
教学重点:
理解并掌握同角三角函数关系式.
教学难点:
已知某角的一个三角函数值,求它的其余各三角函数值时正负号的选择;
教学用具:
直尺、投影仪.
教学步骤:
(1)在应用平方关系时,其结果不唯一,注意根据角所在的象限来取舍;
(2)在学习中必须注意“同角”这一前提,只有在这一前提下都能使用公式;
(3)注意公式的等价变形和常用数值:
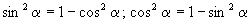 ;
;
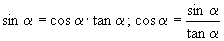 ;
;
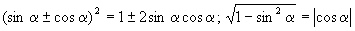 .
.
(4)证明恒等式要注意等价变形,不能随意扩大和缩小范围;
(5)化简要尽使结果只存在一个角,尽是使根式下,分母上不含有三角函数,其结果还要依题意而定.
教学设计方案(一)
同角三角函数的基本关系式
教学目标:
1.掌握同角三角函数之间的三组常用关系,平方关系、商数关系、倒数关系.
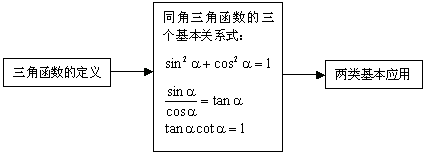
重点是三个公式的推导和应用.
(1)已知 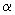 的三角函数值中的一个,表示它的其他三角函数值;
的三角函数值中的一个,表示它的其他三角函数值;
(2)化简三角函数式;
(3)证明简单的三角恒等式.
难点是公式的应用.
(1)利用 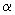 的某一三角函数值求
的某一三角函数值求
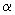 的其他三角函数值;
的其他三角函数值;
(2)三角恒等式的证明,证明恒等式可从左向右,也可从右向左,等价变形;
(3)接受切化弦的思想,及恒等变形中等价转化的思想;
(4)化简是最基本的解题思想,结果要求最简形式.
4.4 同角三角函数的基本关系式
教学目标
(1)掌握同角三角函数之间的三组常用关系,平方关系、商数关系、倒数关系; (2)会运用同角三角函数之间的关系求三角函数值或化简三角式;应用同角三角函数关系,化简三角式(求值);并能证明简单的三角恒等式; (3)牢固掌握同角三角函数的三个关系式并能灵活运用于解题,提高学生分析、解决三角问题的思维能力. (4)通过同角三角函数的基本关系学习,提示事物之间的普通联系规律,培养学生辩证唯物主义要观.
教学建议
16. 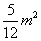 .
.
提示:原式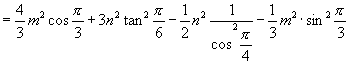
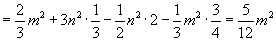 .
.
15. 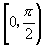 .
.
提示:由 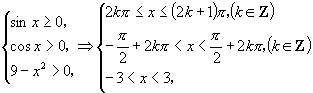
得 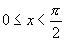 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com