
1.设置情境
与代数式的化简求值一样,我们常会遇到大量的结构比较复杂的三角式让你求值,如:“已知
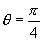 ,求三角式
,求三角式
 的值.”就是这样的问题,如果能在求值之前,把三角式进行化简后再求值,那将是非常理想的事.本节课我们就化简、恒等变形等题型与同学们一同展开讨论.
的值.”就是这样的问题,如果能在求值之前,把三角式进行化简后再求值,那将是非常理想的事.本节课我们就化简、恒等变形等题型与同学们一同展开讨论.
2.证明简单的三角恒等式.
教学重点:
理解并掌握同角三角函数关系式.
教学难点:
(1)三角函数式的化简;(2)证明三角恒等式.
教学用具:
投影仪
教学过程:
1.应用同角三角函数关系,化简三角式(求值).
6.略解:
由 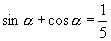 ,平方得,
,平方得,
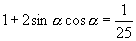 ,
,
∴ 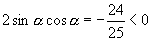
∵  是三角形内角
是三角形内角
∴只有 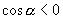
∴ 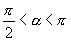 ,
,
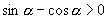
由 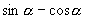
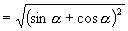
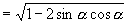
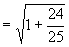
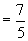
及 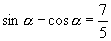 ,联立,得:
,联立,得:
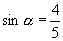 ,
,
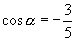 ,
,
∴ 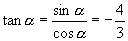
教学设计方案(二)
同角三角函数的基本关系式
教学目标:
6.已知  是三角形的内角,
是三角形的内角,
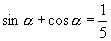 ,求
,求
 值.
值.
参考答案:1.D; 2.B; 3.1; 4.  ; 5.3; 6.
; 5.3; 6.
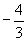
注:4.略解:原式 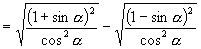
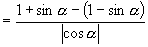
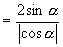
∵  在第二象限
在第二象限
∴ 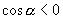
∴ 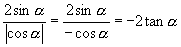 .
.
5.已知 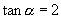 ,求
,求
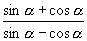 的值.
的值.
4.化简 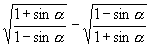 ,其中
,其中
 为第二象限角.
为第二象限角.
3.化简 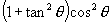
2.若 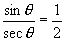 ,则
,则
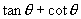 的值是( )
的值是( )
A.-2
B.2 C.±2
D. 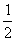
1.已知 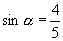 ,
,
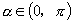 ,则
,则
 等于( )
等于( )
A. 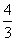 B.
B. 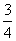 C.
C. 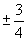 D.
D. 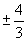
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com