
2.已知 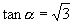 ,
,
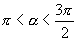 ,那么
,那么
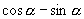 的值是( ).
的值是( ).
A. 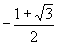 B.
B. 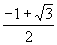 C.
C. 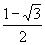 D.
D. 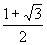
1.已知 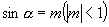 ,
,
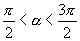 ,那么
,那么
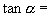 ( ).
( ).
A.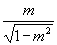 B.
B. 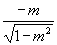 C.
C. 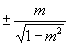 D.
D. 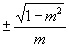
6.解:消 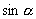 、
、
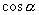 事实上:
事实上:
由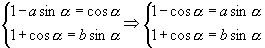
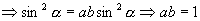
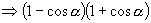
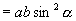 (其中
(其中 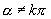 ,
,
 否则
否则
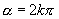 时或
时或
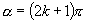 ,
,
 时,条件均不能同时成立)
时,条件均不能同时成立)
典型例题
例1 已知 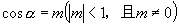 ,试用
,试用
 表示其他五种三角函数.
表示其他五种三角函数.
分析:本题首先应注意对
 进行分类,再利用同角三角函数的关系求之.
进行分类,再利用同角三角函数的关系求之.
解:由于 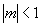 ,且
,且
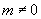 ,所以其他五种三角函数都有意义.
,所以其他五种三角函数都有意义.
(1)当  在第一、二象限时,
在第一、二象限时,
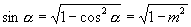 ,
, 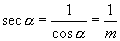 ,
,
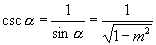 ,
,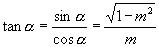 ,
,
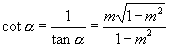 .
.
(2)当  在第三、四象限时,
在第三、四象限时,
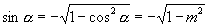 ,
,
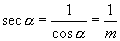 ,
, 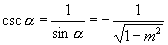 ,
,
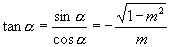 ,
, 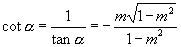 .
.
说明:解决此类问题时,应注意尽可能地确定
 所在的象限,以便确定三角函数的符号.另外,在用一个角的三角函数值表示其他几个三角函数值时,应尽可能少地使用平方关系.
所在的象限,以便确定三角函数的符号.另外,在用一个角的三角函数值表示其他几个三角函数值时,应尽可能少地使用平方关系.
例2 已知 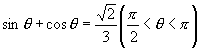 ,求
,求
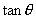 的值.
的值.
分析:本题的解题思路入口处较宽,下面给出一种化切为弦的求法.
解:将已知等式两边平方得
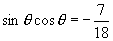 .
.
由于 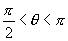 ,所以
,所以
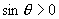 ,
,
 ,从而
,从而
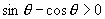 ,故
,故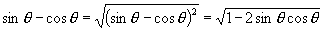
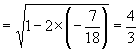 .
.
解方程组 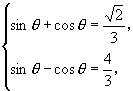 解得
解得
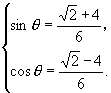
故 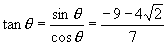 .
.
说明:对于本题还可以有其他多种解法,有兴趣的读者不妨一试,但值得注意的是,对本题如若解题时不很细主,则很容易发生误解,如以下这种解法:
由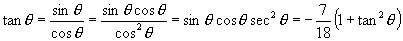 .
.
即 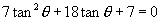 ,解得
,解得
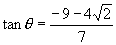 或
或
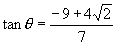 .
.
你能看出其中的错误吗?
例3 化简 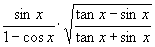 .
.
分析:对本题一般可采取化切为弦的办法进行化简.
解:原式 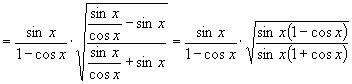
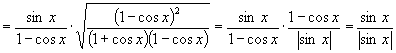
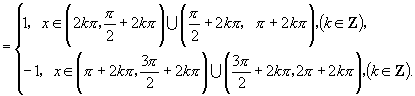
说明:化简三角函数式所得的最后结果,应满足以下要求:①函数的种类要最少;②项数要最少;③函数次数要最低;④能求出数值的要求出数值;⑤尽量使分母不含三角函数;⑥尽量使分母不含根式.
例4 求证 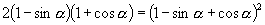 .
.
分析:对本题,可多角度地探究其证法.
证法一:左边 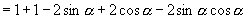
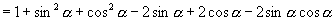
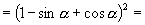 右边.
右边.
证法二:右边-左边
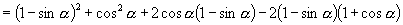
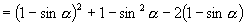
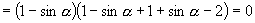
证法三:命 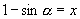 ,
,
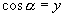 ,消
,消
 得
得
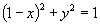 ,即
,即
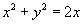 ,
,
左边 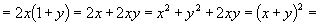 右边.
右边.
证法四:构造关于
 的方程
的方程
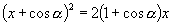 ,即
,即
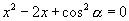 ,解之得
,解之得
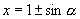 ,将其一根
,将其一根
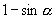 代入第一个方程,即有
代入第一个方程,即有
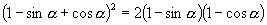 .
.
说明:在本题的上述四种不同的证法当中,均体现了一种转化与化归的数学思想方法.
扩展资料
正弦、余弦
三角学开创之初,希腊人思考的是定圆各中心角所对应的弦长﹝全弦﹞。如托勒密﹝约85-165﹞把圆周﹝角﹞分成360份,把直径分为120份,然后对于圆心角∠COB求对应弦的长﹝直径的1/120为弦的度量单位﹞。而印度人则不同,他们研究一个角的倍角所对弦的一半,即∠AOB对应的半弦长BD。例如,印度为我们知道的最早的数学家阿利耶毗陀﹝476-550﹞,他把圆周分成 360×60=21600﹝份﹞,然后根据公式C﹝周长﹞=2πr,π  3.141,求得圆半径的近似值3438﹝份﹞,再求出各圆周角所对的半弦的长﹝以半径的1/3438为度量单﹞,这与现今的正弦﹝sine﹞概念接近了一步,且已有弧度制思想的雏形。当时阿利耶毗陀称此半弦为「jlva」,意即「弓弦」,这个词阿拉伯人音译为「dschiba」,后经多次转抄,误作「dschiab」,意思是胸膛,海湾或凹处,已与原意有出入。至12世纪,意大利人T‧柏拉图又将此字译成拉丁文sinus﹝胸当﹞,此即今日正弦一词的来由。
3.141,求得圆半径的近似值3438﹝份﹞,再求出各圆周角所对的半弦的长﹝以半径的1/3438为度量单﹞,这与现今的正弦﹝sine﹞概念接近了一步,且已有弧度制思想的雏形。当时阿利耶毗陀称此半弦为「jlva」,意即「弓弦」,这个词阿拉伯人音译为「dschiba」,后经多次转抄,误作「dschiab」,意思是胸膛,海湾或凹处,已与原意有出入。至12世纪,意大利人T‧柏拉图又将此字译成拉丁文sinus﹝胸当﹞,此即今日正弦一词的来由。
1631年邓玉涵﹝1576-1630﹞汤若望﹝1591-1666﹞与徐光启﹝1562-1633﹞编译的《大测》一书,将sinus译成正半弦或前半弦,简称正弦,此即我国正弦一词的来源。正弦、余弦﹝cosine﹞函数的现代定义起源于欧拉。
正割、余割起源
正割﹝secant﹞及余割﹝cosecant﹞这两个概念由伊朗数学家、天文学家阿布尔─威发﹝940-998﹞首先引入。 sec这个略号是1626年荷兰数基拉德﹝1595-1630﹞在他的《三角学》中首先使用,后经欧拉采用才得以通行。正割、余割函数的现代定义亦是由欧拉给出的。
探究活动
相关的三角比
已知锐角 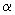 的正弦值为
的正弦值为
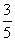 ,你能推出哪些与
,你能推出哪些与
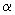 相关的三角比的值?
相关的三角比的值?
分析与解:下面是一些答案.
(1) 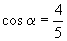 . (2)
. (2) 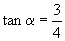 .
.
(3) 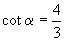 . (4)
. (4) 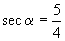 .
.
(5) 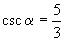 . (6)
. (6) 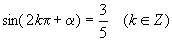 .
.
(7) 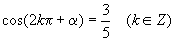 .
.
(8) 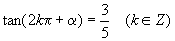 .
.
习题精选
5.当 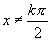 ,
,
 时,
时,
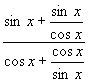
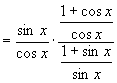
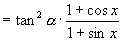
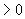
∴选A
4.由 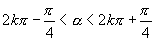 ,
,
 ,
,
得 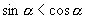 且
且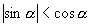
原式 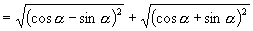
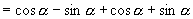
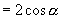
∴选C
3.∵ 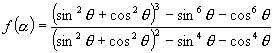
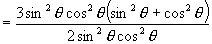
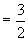
∴ 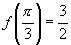 .
.
2.原式 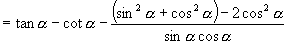
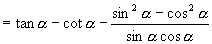
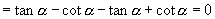
1.(1)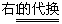
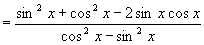
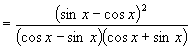
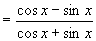
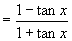
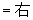
(2)∵左-右 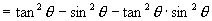
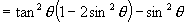
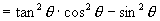
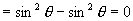
∴左=右
(3)左 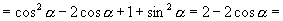 右 ∴命题成立
右 ∴命题成立
(4)∵ 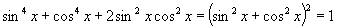
∴ 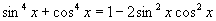
6.已知 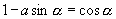 ,
,
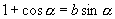 求证
求证 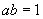
参考答案:
5.若 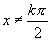 ,
,
 ,则
,则
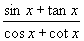 的值( )
的值( )
A.恒正 B.恒负 C.恒为非负 D.恒为非正
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com