
13.(08考题)若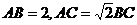 ,则
,则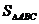 的最大值 ▲
的最大值 ▲
[解析]本题主要考查灵活运用有关的基础知识(阿波罗尼期圆)解决问题的能力.本题属难题.[答案]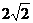 .
.
09示例12.(08考题13.)
2010示例12.( 08考题13.)
2010示例13.在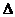 ABC中,
ABC中,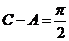 ,
, 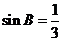 .
.
(1)求 值;(2)设
值;(2)设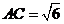 ,求
,求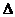 ABC的面积.
ABC的面积.
[解析]本题主要考查三角恒等变换、正弦定理等基础知识,考查运算求解能力.本题属容易题.
解析:三角已成为必考题型之一,一个填空,一个解答!(08年考了2个解答题,有点怪)
3.未考点:对数及对数函数、幂函数(A级),关注!
思考:
◆函数还能怎么考?
提醒:考过的函数还可能再考,如09年20题,重视!
附:(02年全国理)21.设a为实数,函数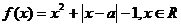
(1) 讨论f(x)函数的奇偶性
(2) 求函数f(x)的最小值。
(05江苏22)已知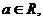 函数
函数
(Ⅰ)当a=2时,求使f(x)=x成立的x的集合;
(Ⅱ)求函数y=f (x)在区间[1,2]上的最小值.
(06江苏20)设a为实数,设函数 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=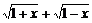 ,求t的取值范围,并把f(x)表示为t的函数m(t);(Ⅱ)求g(a);(Ⅲ)试求满足
,求t的取值范围,并把f(x)表示为t的函数m(t);(Ⅱ)求g(a);(Ⅲ)试求满足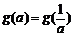 的所有实数a
的所有实数a
(令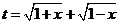 ,→函数
,→函数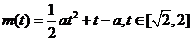 )
)
(07广东) 已知a是实数,函数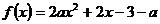 ,如果函数
,如果函数 在区间
在区间 上有零点,求a的取值范围.
上有零点,求a的取值范围.
|
3.基本初等 函数Ⅱ(三角函数)、三角恒等变换 |
三角函数的概念 |
|
√ |
|
|
同角三角函数的基本关系式 |
|
√ |
|
|
|
正弦函数、余弦函数的诱导公式 |
|
√ |
|
|
|
正弦函数、余弦函数、正切函数的图象与性质 |
|
√ |
|
|
函数 的图象与性质 的图象与性质 |
√ |
|
|
|
|
两角和(差)的正弦、余弦及正切 |
|
|
√ |
|
|
二倍角的正弦、余弦及正切 |
|
√ |
|
|
|
积化和差、和差化积及半角公式 |
√ |
|
|
(08考题1).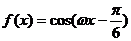 最小正周期为
最小正周期为 ,其中
,其中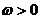 ,则
,则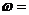
09示例1.已知函数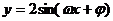
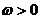 在区间
在区间 上的图象如图,则
上的图象如图,则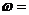
[解析]本题主要考查三角函数的图象与周期.本题属容易题.
 [答案]2.
[答案]2.
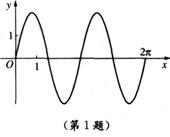
09考题4.函数 为常数,
为常数,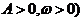 在闭区间
在闭区间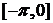 上的图象如图所示,则
上的图象如图所示,则 ★ .
★ .

2010示例1 (09考题4)
(08考题15)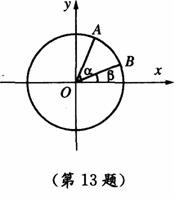 如图,在平面直角坐标系
如图,在平面直角坐标系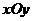 中,以
中,以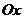 轴为始边作两个锐角
轴为始边作两个锐角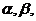 它们的终边分别与单位圆交于
它们的终边分别与单位圆交于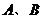 两点.已知
两点.已知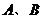 两点的横坐标分别是
两点的横坐标分别是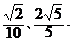
(1)求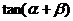 的值;
的值;
(2)求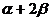 的值.
的值.
[解析]本题主要考查三角函数的基本概念,以及两角和(差)的三角函数公式的简单运用等基础知识,
考查运算求解能力.本题属容易题.
(得分:11分)
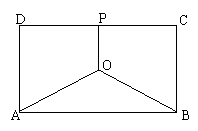 (08考题17)(14分)某地有三家工厂,分别位于矩形ABCD的顶点A、B及CD的中点P处,已知AB=20km,BC=10km,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A、B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP,设排污管道的总长为ykm。
(08考题17)(14分)某地有三家工厂,分别位于矩形ABCD的顶点A、B及CD的中点P处,已知AB=20km,BC=10km,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A、B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP,设排污管道的总长为ykm。
(1)按下列要求写出函数关系式:
①设∠BAO=θ(rad),将y表示成θ的函数关系式;
②设OP=x(km),将y表示成x的函数关系式;
(2)请你选用(1)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短。
(得分:5.8分)
09示例13.(08考题15.)
09考题15:
设向量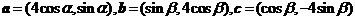
(1)若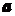 与
与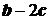 垂直,求
垂直,求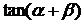 的值;
的值;
(2)求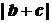 的最大值;
的最大值;
(3)若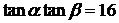 ,求证:
,求证: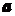 ∥
∥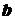 .(得分:11.48分)
.(得分:11.48分)
|
4.正弦定理、余弦定理及其应用 |
|
√ |
|
2.难度:以中、难为主;
1.考法:以含参函数为载体,重点考查考生的代数推、证能力;重点考查四大数学思想(分类讨论、数形结合、等价转化、函数方程);
20.(08考题) (16分)
若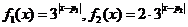 ,
,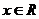 ,
, 为常数,且
为常数,且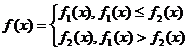
(1)求 对所有实数
对所有实数 成立的充要条件(用
成立的充要条件(用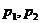 表示)
表示)
(2)设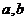 为两实数,
为两实数,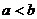 且
且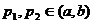 若
若
求证: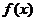 在区间
在区间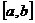 上的单调增区间的长度和为
上的单调增区间的长度和为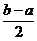 (闭区间
(闭区间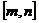 的长度定义为
的长度定义为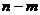 )(得分:2.2分)
)(得分:2.2分)
09考题10.已知 ,函数
,函数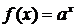 ,若实数
,若实数 满足
满足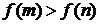 ,则
,则 的大小关系为 ★ .
的大小关系为 ★ .
09考题19.(本小题满分16分)
按照某学者的理论,假设一个人生产某产品单件成本为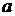 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为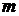 元,则他的满意度为
元,则他的满意度为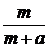 ;如果他买进该产品的单价为
;如果他买进该产品的单价为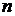 元,则他的满意度为
元,则他的满意度为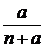 .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为 和
和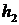 ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为 .
.
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为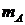 元和
元和 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为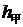 ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为
(1)
求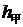 和
和 关于
关于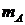 、
、 的表达式;当
的表达式;当 时,求证:
时,求证: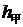 =
= ;
;
(2)
设 ,当
,当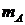 、
、 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
(3)
记(2)中最大的综合满意度为 ,试问能否适当选取
,试问能否适当选取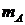 、
、 的值,使得
的值,使得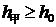 和
和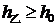 同时成立,但等号不同时成立?试说明理由。(得分:7.2分)
同时成立,但等号不同时成立?试说明理由。(得分:7.2分)
09考题20. (本小题满分16分)
设a为实数,函数f (x)=2x2+(x−a)|x−a|.
(1)若f (0)≥1,求a的取值范围;
(2)求f (x)的最小值;
(3)设函数h(x)=f (x),xÎ(a,+¥),直接写出(不需给出演算步骤)不等式h(x)≥1的解集.(得分:4.14分)
解析:函数向来是高考的热点,且都是压轴题,这与命题组成员的喜好不无关系!
3.未考点:并集、补集,关注!
|
2.函数概念 与基本初 等函数Ⅰ |
函数的概念 |
|
√ |
|
|
函数的基本性质 |
|
√ |
|
|
|
指数与对数 |
|
√ |
|
|
|
指数函数的图象与性质 |
|
√ |
|
|
|
对数函数的图象与性质 |
|
√ |
|
|
|
幂函数 |
√ |
|
|
|
|
函数与方程 |
√ |
|
|
|
|
函数模型及其应用 |
|
√ |
|
2.难度:易、中、难皆可能;
1.考法:常与其它知识组合在一起命题;
08、09考题 解析
A.必做题部分
|
1.集合 |
集合及其表示 |
√ |
|
|
|
子集 |
|
√ |
|
|
|
交集、并集、补集 |
|
√ |
|
08考题4: ,则集合A
,则集合A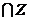 中有 个元素
中有 个元素
[解析]本题主要考查一元二次不等式的解法、集合的运算等基础知识.本题属容易题.[答案] 6.
09示例4:(同08考题4)
09考题11:已知集合 ,
, ,若
,若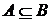 则实数
则实数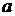 的取值范围是
的取值范围是 ,其中
,其中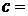 .
.
2010示例4:(09示例4:08考题4)
解析:集合作为一个独立一章必考无疑;
22.(本小题满分14分)
已知直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点, 是线段
是线段 上的一点,
上的一点, ,且点M在直线
,且点M在直线 上
上
(1)求椭圆的离心率;
(2)若椭圆的焦点关于直线 的对称点在单位圆
的对称点在单位圆 上,求椭圆的方程。
上,求椭圆的方程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com