
(三)教学过程
1.设置情境
本节课,我们将综合应用正切函数的性质,讨论泛正切函数的性质.
2.探索研究
(1)复习引入
师:上节课我们学习了正切函数的作图及性质,下面请同学们复述一下正切函数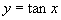 的主要性质
的主要性质
生:正切函数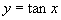 ,定义域为
,定义域为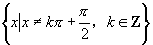 ;值域为
;值域为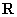 ;周期为
;周期为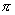 ;单调递增区间
;单调递增区间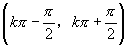 ,
, .
.
(2)例题分析
[例1]判断下列函数的奇偶性:
(1)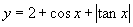 ; (2)
; (2)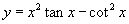 ;
;
分析:根据函数的奇偶性定义及负角的诱导公式进行判断.
解:(1)∵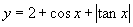 的定义域为
的定义域为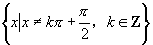 关于原点对称.
关于原点对称.
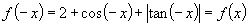
∴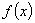 为偶函数
为偶函数
(2)∵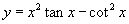 的定义域为
的定义域为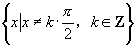 关于原点对称,且
关于原点对称,且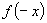
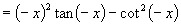
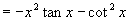
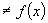 且
且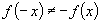 ,
,
∴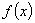 即不是奇函数又不是偶函数.
即不是奇函数又不是偶函数.
说明:函数具有奇、偶性的必要条件之一是定义域关于原点对称,故难证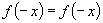 或
或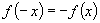 成立之前,要先判断定义域是否关于原点对称.
成立之前,要先判断定义域是否关于原点对称.
[例2]求下列函数的单调区间:
(1)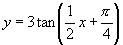 ; (2)
; (2)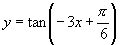 .
.
分析:利用复合函数的单调性求解.
解:(1)令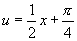 ,则
,则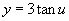
∵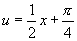 为增函数,
为增函数,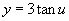 在
在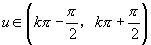 ,
, 上单调递增,
上单调递增,
∴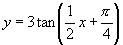 在
在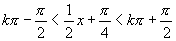 ,即
,即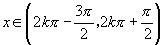 上单调递增.
上单调递增.
(2)令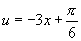 ,则
,则
∵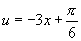 为减函数,
为减函数, 在
在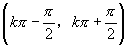
 上单调递增,
上单调递增,
∴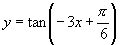 在
在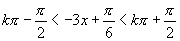 上单调递减,即
上单调递减,即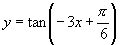 在
在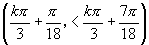 上单调递减.
上单调递减.
[例3]求下列函数的周期:
(1)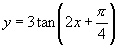 (2)
(2)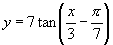 .
.
分析:利用周期函数定义及正切函数最小正周期为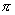 来解.
来解.
解:(1)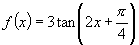
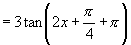
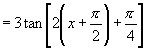
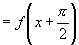
∴周期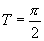
(2)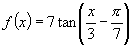
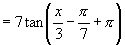
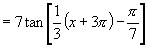
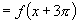
∴周期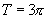
师:从上面两例,你能得到函数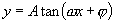 的周期吗?
的周期吗?
生:周期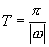
[例4]有两个函数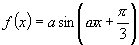 ,
,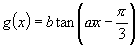 (其中
(其中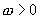 ),已知它们的周期之和为
),已知它们的周期之和为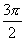 ,且
,且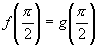 ,
,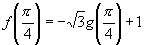 ,求
,求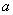 、
、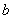 、
、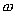 的值.
的值.
解:∵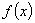 的周期为
的周期为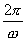 ,
,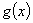 的周期为
的周期为 ,由已知
,由已知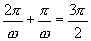 得
得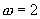
∴函数式为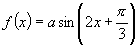 ,
,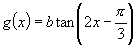 ,由已知,得方程组
,由已知,得方程组

即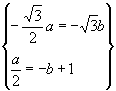 解得
解得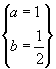
∴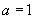 ,
,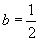 ,
,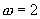
[参考例题]求函数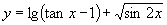 的定义域.
的定义域.
解:所求自变量 必须满足
必须满足
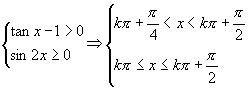 (
( )
)
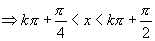 (
( )
)
故其定义域为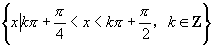
3.演练反馈(投影)
(1)下列函数中,同时满足①在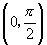 上递增;②以
上递增;②以 为周期;③是奇函数的是( )
为周期;③是奇函数的是( )
A.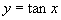 B.
B.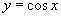 C.
C.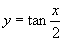 D.
D.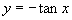
(2)作出函数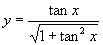
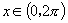 ,且
,且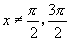 的简图.
的简图.
(3)函数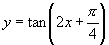 的图像被平行直线_______隔开,与
的图像被平行直线_______隔开,与 轴交点的横坐标是__________,与
轴交点的横坐标是__________,与 轴交点的纵坐标是_________,周期________,定义域__________,它的奇偶性是_____________.
轴交点的纵坐标是_________,周期________,定义域__________,它的奇偶性是_____________.
参考答案:(1)C.
(2)
如图
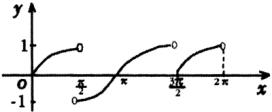
(3)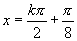 (
( );
);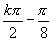 ,(
,( );1;
);1;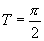 ;
;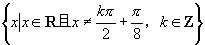 ;非奇非偶函数.
;非奇非偶函数.
4.总结提炼
(1)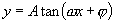 的周期公式
的周期公式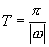 ,它没有极值,正切函数在定义域上不具有单调性(非增函数),了不存在减区间.
,它没有极值,正切函数在定义域上不具有单调性(非增函数),了不存在减区间.
(2)求复合函数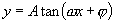 的单调区间,应首先把
的单调区间,应首先把 、
、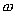 变换为正值,再用复合函数的单调性判断法则求解.
变换为正值,再用复合函数的单调性判断法则求解.
(二)教学目标
运用正切函数图像及性质解决问题.
(四)板书设计
|
课题…… 1.用正切线作正切函数图像 2.正切函数的性质 |
例1 例2 演练反馈 |
总结提炼 |
4.10 正切函数的图象和性质
第二课时
(三)教学过程
1.设置情境
正切函数是区别于正弦函数的又一三角函数,它与正弦函数的最大区别是定义域的不连续性,为了更好研究其性质,我们首先讨论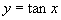 的作图.
的作图.
2.探索研究
师:请同学们回忆一下,我们是怎样利用单位圆中的正弦线作出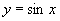 图像的.
图像的.
生:在单位圆上取终边为 (弧度)的角,作出其正弦线
(弧度)的角,作出其正弦线 ,设
,设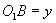 ,在直角坐标系下作点
,在直角坐标系下作点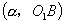 ,则点
,则点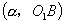 即为
即为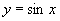 图像上一点.
图像上一点.
师:这位同学讲得非常好,本节课我们也将利用单位圆中的正切线来绘制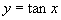 图像.
图像.
(1)用正切线作正切函数图像
师:首先我们分析一下正切函数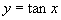 是否为周期函数?
是否为周期函数?
生:∵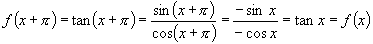
∴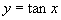 是周期函数,
是周期函数,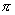 是它的一个周期.
是它的一个周期.
师:对,我们还可以证明,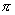 是它的最小正周期.类似正弦曲线的作法,我们先作正切函数在一个周期上的图像,下面我们利用正切线画出函数
是它的最小正周期.类似正弦曲线的作法,我们先作正切函数在一个周期上的图像,下面我们利用正切线画出函数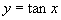 ,
,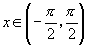 的图像.
的图像.
作法如下:①作直角坐标系,并在直角坐标系 轴左侧作单位圆.
轴左侧作单位圆.
②把单位圆右半圆分成8等份,分别在单位圆中作出正切线.
③找横坐标(把 轴上
轴上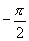 到
到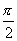 这一段分成8等份).
这一段分成8等份).
④找纵坐标,正切线平移.
⑤连线.
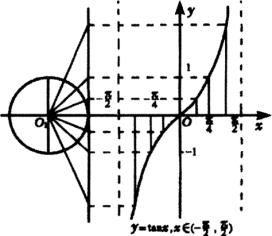
图1
根据正切函数的周期性,我们可以把上述图像向左、右扩展,得到正切函数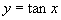 ,
, 且
且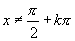 (
( )的图像,并把它叫做正切曲线(如图1).
)的图像,并把它叫做正切曲线(如图1).
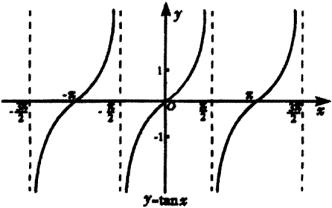
图2
(2)正切函数的性质
请同学们结合正切函数图像研究正切函数的性质:定义域、值域、周期性、奇偶性和单调性.
①定义域: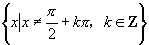
②值域
由正切曲线可以看出,当 小于
小于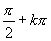 (
( )且无限亲近于
)且无限亲近于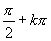 时,
时,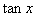 无限增大,即可以比任意给定的正数大,我们把这种情况记作
无限增大,即可以比任意给定的正数大,我们把这种情况记作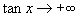 (读作
(读作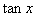 趋向于正无穷大);当
趋向于正无穷大);当 大于
大于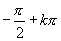 且无限接近于
且无限接近于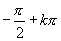 ,
,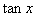 无限减小,即取负值且它的绝对值可以比任意给定的正数大,我们把这种情况记作
无限减小,即取负值且它的绝对值可以比任意给定的正数大,我们把这种情况记作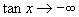 (读作
(读作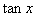 趋向于负无穷大).这就是说,
趋向于负无穷大).这就是说,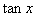 可以取任何实数值,但没有最大值、最小值.
可以取任何实数值,但没有最大值、最小值.
因此,正切函数的值域是实数集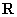 .
.
③周期性
正切函数是周期函数,周期是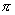 .
.
④奇偶性
∵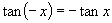 ,∴正切函数是奇函数,正切曲线关于原点
,∴正切函数是奇函数,正切曲线关于原点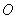 对称.
对称.
⑤单调性
由正切曲线图像可知:正切函数在开区间(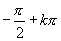 ,
,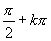 ),
), 内都是增函数.
内都是增函数.
(3)例题分析
[例1]求函数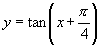 的定义域.
的定义域.
解:令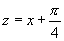 ,那么函数
,那么函数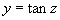 的定义域是
的定义域是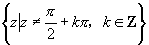
由 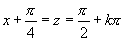 ,可得
,可得 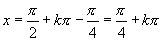
所以函数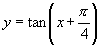 的定义域是
的定义域是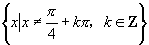
[例2]不通过求值,比较下列各组中两个正切函数值的大小:
(1)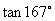 与
与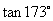 ;
;
(2)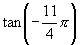 与
与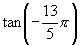 .
.
解:(1)∵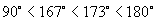
又 ∵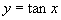 ,在
,在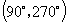 上是增函数
上是增函数
∴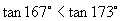
(2)∵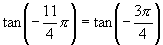
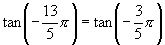
又 ∵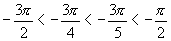 ,函数
,函数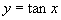 ,
,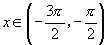 是增函数,
是增函数,
∴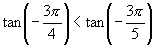 即
即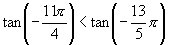 .
.
说明:比较两个正切型实数的大小,关键是把相应的角诱导到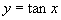 的同一单调区间内,利用
的同一单调区间内,利用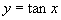 的单调递增性来解决.
的单调递增性来解决.
3.演练反馈(投影)
(1)直线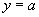 (
(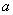 为常数)与正切曲线
为常数)与正切曲线 (
(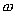 为常数且
为常数且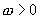 )相交的相邻两点间的距离是( )
)相交的相邻两点间的距离是( )
A.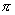 B.
B.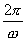 C.
C. D.与
D.与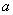 值有关
值有关
(2)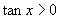 是
是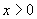 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
(3)根据三角函数的图像写出下列不等式成立的角 集合
集合
①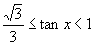 ②
②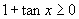
参考答案:
(1)C.注: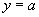 与
与 相邻两点之间距离即为周期长
相邻两点之间距离即为周期长
(2)D.注:由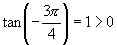 ,但
,但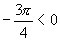 ,反之
,反之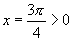 ,但
,但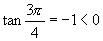
(3)①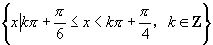
②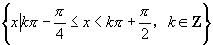
4.总结提炼
(1)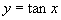 的作图是利用平移正切线得到的,当我们获得
的作图是利用平移正切线得到的,当我们获得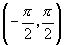 上图像后,再利用周期性把该段图像向左右延伸、平移。
上图像后,再利用周期性把该段图像向左右延伸、平移。
(2)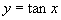 性质.
性质.
|
定义域 |
值域 |
周期 |
奇偶性 |
单调增区间 |
对称中心 |
渐近线方程 |
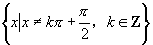 |
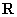 |
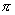 |
奇函数 |
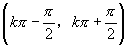  |
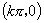  |
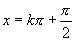 , , |
(二)教学目标
1.会用“正切线”和“单移法”作函数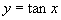 的简图.
的简图.
2.掌握正切函数的性质及其应用.
17.它的减区间即函数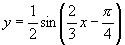 的增区间,由
的增区间,由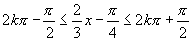 ,得
,得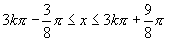 (
( ),即减区间为
),即减区间为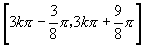 (
( ),同样可求增区间为
),同样可求增区间为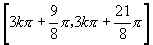 (
( ).
).
18.由题意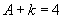 ,
,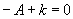 ,∴
,∴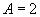 ,
,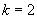 .
.
又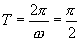 ,∴
,∴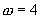 ,∴
,∴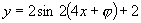 .
.
∵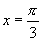 是它的一条对称轴,∴
是它的一条对称轴,∴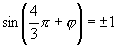 ,
,
∴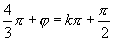 (
( ).
).
从而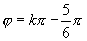 (
( ).
).
∵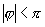 ,∴
,∴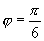 或
或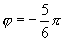 .
.
故该函数的解析式为 ,
,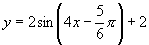 .
.
19.(1)由题中图所示,这段时间的最大温差是30-10=20(℃)
(2)图中从6时到14时的图像是函数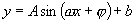 的半个周期的图像,∴
的半个周期的图像,∴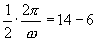 ,解得
,解得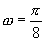 .
.
由图示,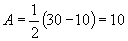 ,
,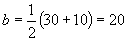 .
.
这时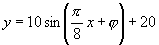 .将
.将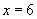 ,
,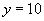 代入上式,可得
代入上式,可得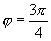 .
.
综上,所求解析式为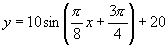 ,
,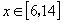 .
.
20.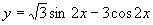
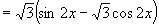
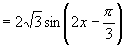 ,
,
(1)由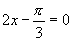 、
、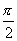 、
、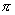 、
、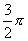 、
、 求出
求出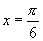 、
、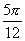 、
、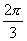 、
、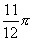 、
、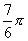 .(可以看到0、
.(可以看到0、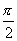 、
、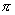 、
、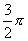 、
、 间隔
间隔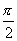 、
、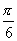 、
、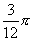 、
、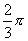 、
、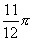 、
、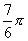 间隔
间隔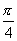 ,所以不需要解五个方程分别求
,所以不需要解五个方程分别求 .)
.)
 |
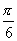 |
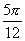 |
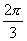 |
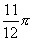 |
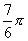 |
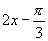 |
0 |
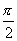 |
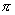 |
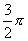 |
 |
 |
0 |
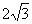 |
0 |
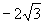 |
0 |
在同一坐标系中,作出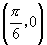 、
、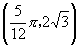 、
、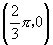 、
、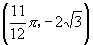 、
、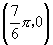 五个点,并用光滑曲线连接起来.
五个点,并用光滑曲线连接起来.
(2)∵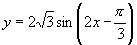 ,
,
∴首先将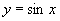 ,
, 的图像所有点向右平移
的图像所有点向右平移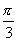 个单位;再把所得的图像上各点的横坐标缩短到原来的
个单位;再把所得的图像上各点的横坐标缩短到原来的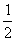 倍(纵坐标不变);最后把所得的图像上所有点的纵坐标伸长到原来的
倍(纵坐标不变);最后把所得的图像上所有点的纵坐标伸长到原来的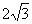 倍(横坐标不变),从而得到
倍(横坐标不变),从而得到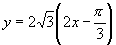 ,
, 的图像,这就是此函数的图像与正弦曲线之间的关系.
的图像,这就是此函数的图像与正弦曲线之间的关系.
(3)周期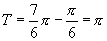 (也可以依据公式
(也可以依据公式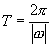 ,
,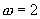 来求);振幅
来求);振幅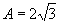 ;依定义
;依定义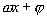 叫相位,
叫相位,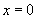 时的
时的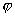 叫做初相,所以初相应该是
叫做初相,所以初相应该是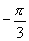 .
.
(4)由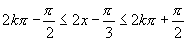 ,
,
得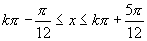 ,
, .
.
由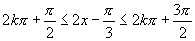 ,
,
得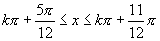 ,
, .
.
∴原函数单调增区间为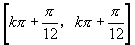 ,
, ;
;
单调减区间为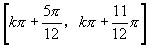 ,
, .
.
21.(1)由数据知函数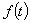 的周期
的周期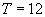 ,振幅
,振幅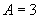 ,
,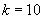 ,
,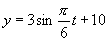 .
.
(2)由题意,该船进出港时,水深应不小于5+6.5=11.5米.
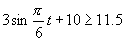 ,
,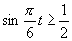 ,
, (
( ),
),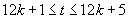 (
( ).
).
在同一天内,取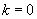 或1,
或1,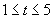 或
或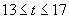 ,
,
∴该船最早能在凌晨1时进港,下午17时出港,在港口最多停留16小时.
4.10 正切函数的图象和性质
教学目标
1.会用单位圆中的正切线画出正切函数的图象;
2.掌握正切函数图象的形状特征和性质,渗透数形结合的思想;
3.通过利用几何法画正切函数图象,了解类比思想,通过练习掌握换元法的运用.
教学建议
知识结构:

重点与难点分析:
本节的重点是正切函数的图象形状及其主要性质(包括定义域、值域、周期性、奇偶性、单调性).正切函数常与其它知识综合运用,图象和性质是具体应用的基础,而函数的性质是由函数图形特征归纳总结的得到的,因此首先了解利用正切线画出函数图象及图象的特征,使图象和性质有效的结合.
本节的难点是利用正切线得到函数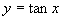 ,
,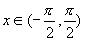 的图象,直线
的图象,直线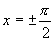 为函数图象的渐近线.选择
为函数图象的渐近线.选择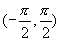 作为基本图象段,学生理解有些困难,给学生说明这一段函数图象是连续的.理解渐近线涉及到极限的知识,学生不易理解,注意用形象的语言加以描述.渐近线
作为基本图象段,学生理解有些困难,给学生说明这一段函数图象是连续的.理解渐近线涉及到极限的知识,学生不易理解,注意用形象的语言加以描述.渐近线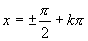 ,
,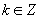 各点由对应着函数在此处无定义,值域无最大值、最小值.充分利用图象和性质的有效结合来解决难点.
各点由对应着函数在此处无定义,值域无最大值、最小值.充分利用图象和性质的有效结合来解决难点.
教法建议:
1.采用类比的思想让学生自主学习,由于学生已经掌握了正弦函数、余弦函数的图象和性质的概念及讨论方法,本节课可让学生回忆正弦函数图象和性质的研究手段和方法的基础上,自主探讨正切函数的图象作法以及性质的归纳,教师在这个过程适当的引入问题让学生解决,对于渐近线等难点问题给与指导和解释.
2.函数图象特征和函数代数性质一一对应,教学中首先要充分利用图形讲清正切曲线的特征,在作图后让学生讨论图象的特征,然后再总结归纳函数的性质,使图象的特征和函数的代数性质有机的结合,例如函数图象的渐近线是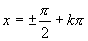 ,
,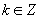 ,函数在各点处无定义,即定义域
,函数在各点处无定义,即定义域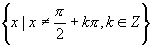 ,值域无最大值、最小值.
,值域无最大值、最小值.
3.在教学中适当通过与正切有关的综合习题,使学生熟悉函数的性质和图象.尤其是与其它知识综合时,通常采取换元法,但要注意正切本身自变量的条件限制,另外可以类比正弦函数的五点法作图,简化正切函数草图的做法,以便辅助解题.
4.10 正切函数的图象和性质
第一课时
16.②、③
15.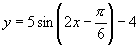
13.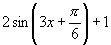 14.
14.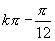 (
( )
)
1.C 2.B 3.D 5.D 6.A 7.D 8.B 9.A 10.A 11.C 12.C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com