
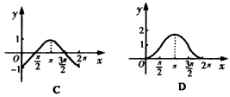
2.下列叙述中正确的个数为( )
①作正弦、余弦函数图像时,单位圆的半径长与x轴上的单位可以不一致。
②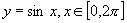 的图像关于点
的图像关于点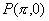 成中心对称图形。
成中心对称图形。
③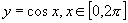 的图像关于直线
的图像关于直线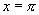 成轴对称图形。
成轴对称图形。
④正弦、余弦函数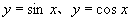 的图像不超出两直线
的图像不超出两直线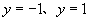 所夹的范围。
所夹的范围。
A.1 B.2 C.3 D.4
1.函数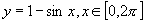 的大致图像是( )
的大致图像是( )
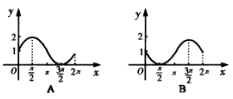
(四)板书设计
|
课题 1.周期函数定义 两点注意: 思考问题① 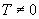 ② 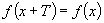 2.最小正周期定义 例1 |
例2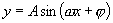 的周期 的周期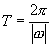 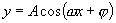 的周期 的周期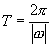 练习反馈 总结提炼 |
思考题:设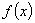 是定义在
是定义在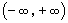 上的以2为周期的周期函数,且是偶函数,当
上的以2为周期的周期函数,且是偶函数,当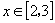 时,
时,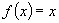 ,求
,求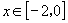 上的表达式
上的表达式
参考答案: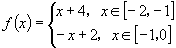
典型例题
例1.求函数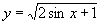 的定义域.
的定义域.
分析:要求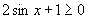 ,即
,即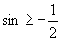 ,因为正弦函数具有周期性,所以只需先根据正弦曲线在一个周期上找出适合条件区间,然后两边加
,因为正弦函数具有周期性,所以只需先根据正弦曲线在一个周期上找出适合条件区间,然后两边加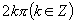 .
.
解:由题意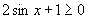 ,
,
即 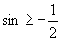 .
.
在一周期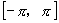 上符合条件的角为
上符合条件的角为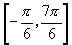 ,
,
∴定义域为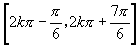
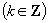 .
.
小结:解题时注意结合正弦曲线,而由于正弦函数的周期性,只需先在一个周期上求范围,这个周期的长度为 ,并非一定取
,并非一定取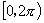 ,而应该是否得到一个完整区间为标准,如本题若在
,而应该是否得到一个完整区间为标准,如本题若在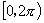 上求范围则分为两段
上求范围则分为两段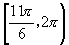 和
和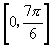 ,不如在
,不如在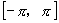 上是完整的一段.
上是完整的一段.
例2.求函数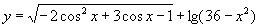 的定义域。
的定义域。
分析:上述函数从形式上看是一个较为复杂的复合函数,它是由三角函数、二次函数、对数函数复合而成。求定义域时,应分清脉络,逐一分析,综合得出结论。
解:欲求函数定义域,则由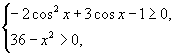
即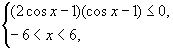 也即
也即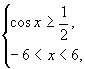
解得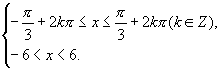
取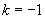 、0、1,可分别得到
、0、1,可分别得到
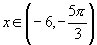 或
或 或
或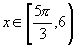 。
。
即所求的定义域为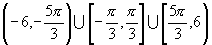 。
。
小结:在解本题时,容易出现的失误是,由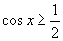 ,得
,得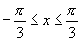 或
或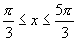 ;或在解不等式组
;或在解不等式组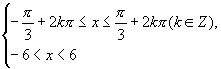 时出现错误,如得出函数的定义域为
时出现错误,如得出函数的定义域为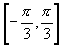 或
或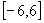 等。
等。
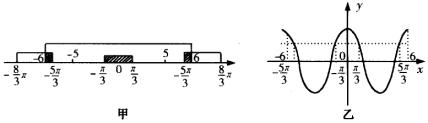
解类似本例的问题,其关键在于求出两个或更多个不等式的公共解。而求公共解,如能借助于图形,由数形结合,往往可以事半功倍。具体方法一般可借助于数轴、单位圆或三角函数的图像来完成。如图甲、乙所示。
例3.求下列函数的值域:
(1)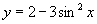 ; (2)
; (2)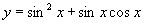 ;
;
(3)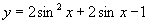 ; (4)
; (4)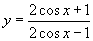 .
.
分析:(1)先利用降幂公式,将其化为一个角的一个三角函数式,再根据三角函数性质求其值域;(2)可利用降幂公式,倍角公式,差角公式,化为一个角的一个三角函数其值域;(3)利用配方法,并结合二次函数、正弦函数的性质求解;(4)从反函数观点出发,借助于余弦函数的有界性求解.
解:(1)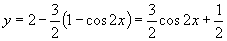 .
.
∵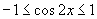 ,∴
,∴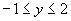 .
.
将其利用降幂公式化为一个角的一个三角函数形式,然后利用三角函数的性质求值域.
(2)
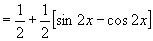
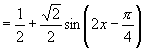
∵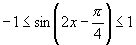 ,
,
∴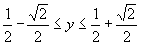 .
.
利用了降幂公式和倍角公式,将其化为一个角的一个三角函数的形式.
(3)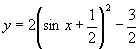 .
.
将其看做关于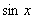 的二次函数,注意到
的二次函数,注意到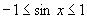 ,
,
∴当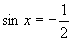 时,
时,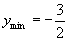 .
.
当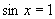 时,
时,
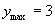 ,
,
∴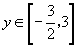 .
.
本题结合了二次函数求极值,但应注意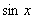 的取值范围.
的取值范围.
(4)由原式得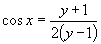 .
.
∵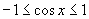 ,∴
,∴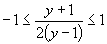 .
.
∴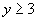 或
或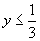 .
.
值域为 .
.
小结: 配方法、化一法、逆求法、有界性法等,是求三角函数值域常用的几种方法.相信你会从此题的求解过程中,领悟到这一点.
例4.求函数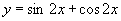 的单调减区间.
的单调减区间.
分析:容易想到将函数转化为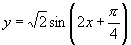 ,换元令
,换元令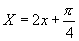 ,进而转化为
,进而转化为 .
.
解: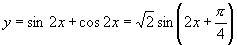 .
.
令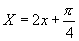 ,则
,则 .
.
由正弦函数的单调性,知
当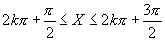 (
( )时,函数递减,
)时,函数递减,
即 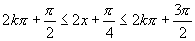 (
( ),
),
∴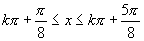 (
( ).
).
∴函数的单调减区间是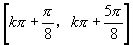 (
( ).
).
小结:本题通过换元,将函数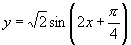 化为
化为 ,充分体现了转化的数学思想.
,充分体现了转化的数学思想.
例5.作函数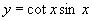 的图像。
的图像。
分析:首先将函数的解析式变形,化为最简形式,然后作函数的图像。
解:当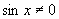 ,即
,即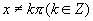 时,有
时,有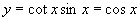 ,即
,即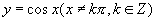 。其图像如图,
。其图像如图,
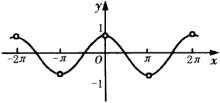
小结:函数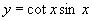 的图像即是
的图像即是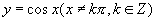 的图像,因此作出
的图像,因此作出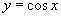 的图像后,要把
的图像后,要把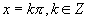 的这些点去掉。
的这些点去掉。
例6.已知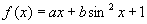 ,(a、b为常数),且
,(a、b为常数),且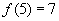 ,求
,求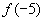 。
。
分析:要求函数值,需知函数解析式,因含a、b两个参数,一个条件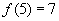 难确定。深入分析
难确定。深入分析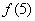 与
与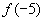 的内在联系,应向函数奇偶性联想。注意到
的内在联系,应向函数奇偶性联想。注意到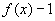 为奇函数,问题自可获解。
为奇函数,问题自可获解。
解:因为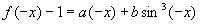
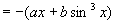
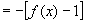 ,所以
,所以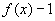 为奇函数,所以
为奇函数,所以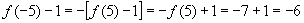 ,
,
所以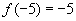 。
。
小结:(1)判断函数奇偶性时应注意“定义域关于原点对称是函数为奇函数或偶函数的必要条件”的应用。
(2)函数奇偶性的确定,可使研究问题的条件增加,从而使问题难度变小,尤其是自变量互为相反数时的函数值关系问题,可考虑奇偶性的应用。
扩展资料
一剪刀剪出一条正弦曲线
把一张纸卷到圆柱形的纸筒面上,卷上几圈.用剪刀斜着将纸筒剪断,再把卷着的纸展开,你就会看到:纸的边缘线是一条波浪形的曲线.
你知道吗?这条曲线就是正弦曲线!下面就来证明这一事实.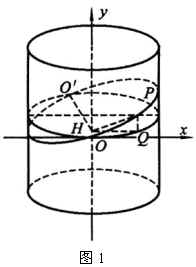
如图1,设纸筒底面半径为1单位长,截面(椭圆面)与底面所成的二面角为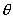 (定值),截口的中心为
(定值),截口的中心为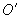 .
.
过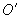 作圆柱的直截面,交截口曲线于两点.取其中一点为
作圆柱的直截面,交截口曲线于两点.取其中一点为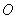 ,在过点
,在过点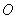 且与圆柱侧面相切的平面内,以点
且与圆柱侧面相切的平面内,以点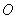 为坐标原点建立直角坐标系,使得
为坐标原点建立直角坐标系,使得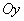 轴是圆柱的一条母线.
轴是圆柱的一条母线.
设点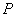 是截口曲线上任意一点,点
是截口曲线上任意一点,点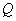 是点
是点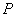 在⊙
在⊙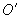 所在平面内的射影,过
所在平面内的射影,过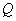 作
作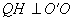 ,垂足为
,垂足为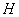 ,连接
,连接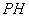 ,则
,则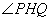 是截面与底面所成二面角的平面角,所以,
是截面与底面所成二面角的平面角,所以,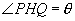 ,又设
,又设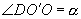 (变量).
(变量).
在图2中,设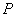 点坐标为
点坐标为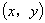 ,以下分别计算
,以下分别计算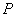 点的横坐标和纵坐标.
点的横坐标和纵坐标.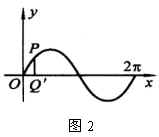
 ,
,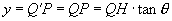 , ①
, ①
而在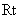 △
△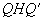 中,
中,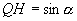 ,所以
,所以
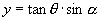 nbsp; ②
nbsp; ②
将①代入②,且令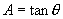 (定值),则有
(定值),则有
这就证明了截口曲线是一条正弦曲线.
(原载《数学通讯》2000年第10期 王方汉 文)
探究活动
试问方程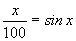 是否有实数解?若有,请求出实数解的个数;若没有,请说明理由.
是否有实数解?若有,请求出实数解的个数;若没有,请说明理由.
分析:可借助函数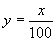 和
和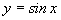 的图像,通过判断图像是否有交点来判定方程是否有实数解.如有交点,可通过讨论交点数来获得实数解的个数.
的图像,通过判断图像是否有交点来判定方程是否有实数解.如有交点,可通过讨论交点数来获得实数解的个数.
解:设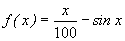 ,因为
,因为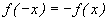 ,且
,且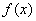 的定义域为R,所以
的定义域为R,所以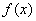 是奇函数,且
是奇函数,且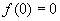 ,所以
,所以 是
是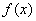 =0的一个解,于是
=0的一个解,于是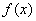 =0的实数解存在且除
=0的实数解存在且除 外是成对出现的.在
外是成对出现的.在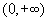 上研究
上研究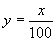 和
和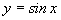 图像交点的情况(参考图)
图像交点的情况(参考图)
因为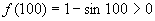 ,且
,且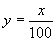 是增函数,而
是增函数,而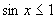 ,所以当x≥100时,方程
,所以当x≥100时,方程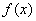 =0无解.
=0无解.
又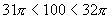 ,从图像中可得知直线
,从图像中可得知直线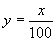 与曲线
与曲线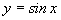 在
在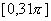 中从0开始每相隔
中从0开始每相隔 会有两个交点,所以,当x≥0时共有32个交点,则当x>0时有31 个交点.
会有两个交点,所以,当x≥0时共有32个交点,则当x>0时有31 个交点.
故原方程有31×2+1=63个解.
习题精选
(三)教学过程
1.设置情境
自然界里存在着许多周而复始的现象,如地球的自转和公转,物理学中的单摆运动和弹簧振动、圆周运动等.数学里从正弦函数、余弦函数的定义可知,角 的终边每转一周又会与原来的位置重合,故
的终边每转一周又会与原来的位置重合,故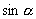 ,
,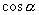 的值也具有周而复始的变化规律.为定量描述这种周而复始的变化规律,今天,我们来学习一个新的数学概念--函数的周期性(板书课题)
的值也具有周而复始的变化规律.为定量描述这种周而复始的变化规律,今天,我们来学习一个新的数学概念--函数的周期性(板书课题)
2.探索研究
(1)周期函数的定义
引导学生观察下列图表及正弦曲线
 |
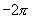 |
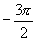 |
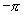 |
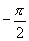 |
0 |
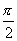 |
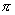 |
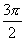 |
 |
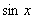 |
0 |
1 |
0 |
-1 |
0 |
1 |
0 |
-1 |
0 |
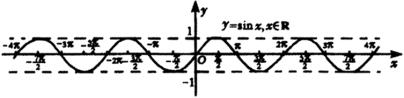
正弦函数值当自变量增加或减少一定的值时,函数值就重复出现.
联想诱导公式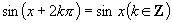 ,若令
,若令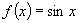 则
则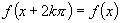 ,由这个例子,我们可以归纳出周期函数的定义:
,由这个例子,我们可以归纳出周期函数的定义:
对于函数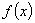 ,如果存在一个非零常数
,如果存在一个非零常数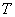 ,使得当
,使得当 取定义域内的每一个值时,都有
取定义域内的每一个值时,都有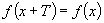 ,那么函数
,那么函数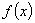 叫做周期函数,非零常数
叫做周期函数,非零常数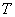 叫做这个函数的周期.
叫做这个函数的周期.
如 ,
,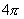 ,…及
,…及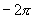 ,
,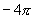 …都是正弦函数的周期.
…都是正弦函数的周期.
注意:周期函数定义中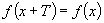 有两点须重视,一是
有两点须重视,一是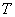 是常数且不为零;二是等式必须对定义域中的每一个值时都成立.
是常数且不为零;二是等式必须对定义域中的每一个值时都成立.
师:请同学们思考下列问题:①对于函数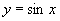 ,
, 有
有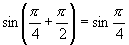 能否说
能否说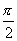 是正弦函数
是正弦函数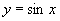 的周期.
的周期.
生:不能说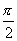 是正弦函数
是正弦函数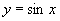 的周期,这个等式虽成立,但不是对定义域的每一个值都使等式
的周期,这个等式虽成立,但不是对定义域的每一个值都使等式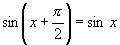 成立,所以不符合周期函数的定义.
成立,所以不符合周期函数的定义.
②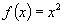 是周期函数吗?为什么
是周期函数吗?为什么
生:若是周期函数,则有非零常数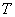 ,使
,使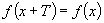 ,即
,即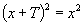 ,化简得
,化简得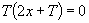 ,∴
,∴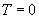 (不非零),或
(不非零),或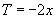 (不是常数),故满足非零常数
(不是常数),故满足非零常数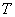 不存在,因而
不存在,因而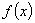 不是周期函数.
不是周期函数.
思考题:若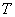 为
为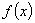 的周期,则对于非零整数
的周期,则对于非零整数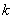 ,
,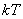 也是
也是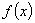 的周期.(课外思考)
的周期.(课外思考)
(2)最小正周期的定义
师:我们知道…,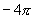 ,
,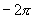 ,
, ,
,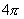 …都是正弦函数的周期,可以证明
…都是正弦函数的周期,可以证明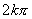 (
(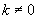 且
且 )是
)是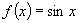 的周期,其中
的周期,其中 是
是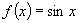 的最小正周期.
的最小正周期.
一般地,对于一个周期函数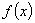 ,如果在它所有的周期中存在一个最小的正数,那么这个最小正数就叫做
,如果在它所有的周期中存在一个最小的正数,那么这个最小正数就叫做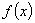 的最小正周期.
的最小正周期.
今后若涉及的周期,如果不加特别说明,一般都是指函数的最小正周期.
依据定义,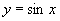 和
和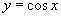 的最小正周期为
的最小正周期为 .
.
(3)例题分析
[例1]求下列函数的周期:
(1)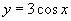 ,
, ; (2)
; (2)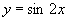 ,
, ;
;
(3)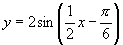 ,
, .
.
分析:由周期函数的定义,即找非零常数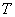 ,使
,使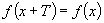 .
.
解:(1)因为余弦函数的周期是 ,所以自变量
,所以自变量 只要并且至少要增加到
只要并且至少要增加到 ,余弦函数的值才能重复取得,函数
,余弦函数的值才能重复取得,函数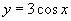 ,
, 的值也才能重复取得,从而函数
的值也才能重复取得,从而函数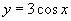 ,
, 的周期是
的周期是 .
.
即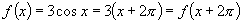 ,∴
,∴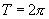
(2)令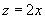 ,那么
,那么 必须并且只需
必须并且只需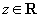 ,且函数
,且函数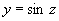 ,
,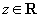 的周期是
的周期是 ,就是说,变量
,就是说,变量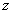 只要并且至少要增加到
只要并且至少要增加到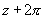 ,函数
,函数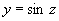 ,
,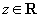 的值才能重复取得,而
的值才能重复取得,而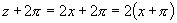 所以自变量
所以自变量 只要并且至少要增加到
只要并且至少要增加到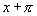 ,函数值就能重复取得,从而函数
,函数值就能重复取得,从而函数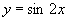 ,
, 的周期是
的周期是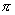 .
.
即 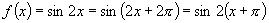
∴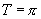
(3)令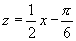 ,那么
,那么 必须并且只需
必须并且只需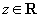 ,且函数
,且函数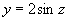 ,
,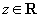 的周期是
的周期是 ,由于
,由于
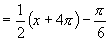 ,所以自变量
,所以自变量 只要并且至少要增加到
只要并且至少要增加到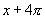 ,函数值才能重复取得,即
,函数值才能重复取得,即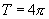 是能使等式
是能使等式 成立的最小正数,从而函数
成立的最小正数,从而函数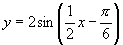 ,
, 的周期是
的周期是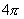 .
.
而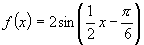
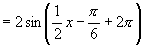
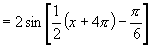
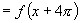
∴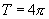
师:从上例可以看出,这些函数的周期仅与自变量 的系数有关,其规律如何?你能否求出函数
的系数有关,其规律如何?你能否求出函数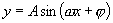 ,
, 及函数
及函数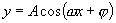 ,
, (其中
(其中 ,
,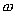 ,
,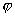 为常数,且
为常数,且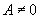 ,
,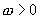 )的周期?
)的周期?
生: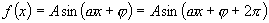
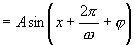
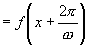
∴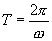 .
.
同理可求得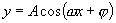 的周期
的周期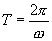 .
.
[例2]求证:
(1)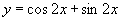 的周期为
的周期为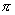 ;
;
(2)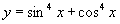 的周期为
的周期为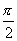 ;
;
(3)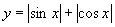 的周期为
的周期为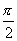 .
.
分析:依据周期函数定义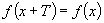 证明.
证明.
证明:(1)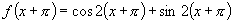
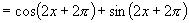
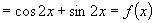
∴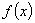 的周期为
的周期为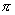 .
.
(2)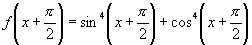
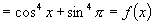
∴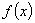 的周期为
的周期为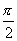 .
.
(3)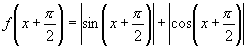
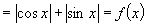
∴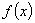 的周期为
的周期为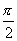 .
.
3.演练反馈(投影)
(1)函数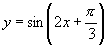 的最小正周期为( )
的最小正周期为( )
A. B.
B.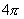 C.
C.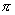 D.
D.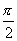
(2)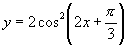 的周期是_________
的周期是_________
(3)求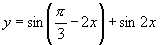 的最小正周期.
的最小正周期.
参考答案:
(1)C;(2)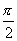
 ∴
∴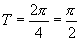
(3)欲求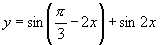 的周期,一般是把三角函数
的周期,一般是把三角函数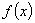 化成易求周期的函数
化成易求周期的函数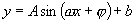 或
或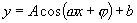 的形式,然后用公式
的形式,然后用公式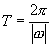 求最小正周期,而化得的一般思路是“多个化一个,高次化一次”,将所给函数化成单角单函数.
求最小正周期,而化得的一般思路是“多个化一个,高次化一次”,将所给函数化成单角单函数.
由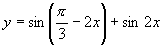
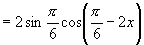
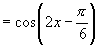
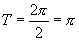
4.总结提炼
(1)三角函数所特有的性质是周期性,周期与最小正周期是不同概念,研究三角函数的周期时,如未特别声明,一般是指它的最小正周期.
(2)设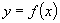 ,
, .若
.若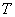 为
为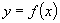 的周期,则必有:①
的周期,则必有:①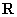 为无限集,②
为无限集,②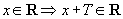 ;③
;③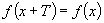 在
在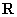 上恒成立.
上恒成立.
(3)只有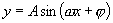 或
或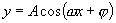 型的三角函数周期才可用公式
型的三角函数周期才可用公式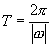 ,不具有此形式,不能套用.如
,不具有此形式,不能套用.如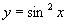 ,就不能说它的周期为
,就不能说它的周期为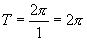 .
.
(二)教学目标
1.理解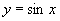 ,
,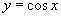 的周期性概念,会求周期.
的周期性概念,会求周期.
2.初步掌握用定义证明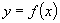 的周期为
的周期为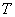 的一般格式.
的一般格式.
(一)教学具准备
直尺、投影仪.
(五)板书设计
|
1.定义域 2.值域 3.最值 4.正负区间 5.零点 例1 |
例2 例3 课堂练习 |
课后思考题:求函数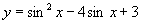 的最大值和最小值及取最值时的
的最大值和最小值及取最值时的 集合
集合
提示:
教学设计示例
4.8 正弦函数、余弦函数的图像和性质(第三课时)
(三)教学过程
1.设置情境
研究函数就是要讨论一些性质,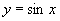 ,
,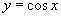 是函数,我们当然也要探讨它的一些属性.本节课,我们就来研究正弦函数、余弦函数的最基本的两条性质.
是函数,我们当然也要探讨它的一些属性.本节课,我们就来研究正弦函数、余弦函数的最基本的两条性质.
2.探索研究
师:同学们回想一下,研究一个函数常要研究它的哪些性质?
生:定义域、值域,单调性、奇偶性、等等.
师:很好,今天我们就来探索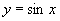 ,
,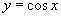 两条最基本的性质--定义域、值域.(板书课题正、余弦函数的定义域、值域.)
两条最基本的性质--定义域、值域.(板书课题正、余弦函数的定义域、值域.)
师:请同学看投影,大家仔细观察一下正弦、余弦曲线的图像.
师:请同学思考以下几个问题:
(1)正弦、余弦函数的定义域是什么?
(2)正弦、余弦函数的值域是什么?
(3)他们最值情况如何?
(4)他们的正负值区间如何分?
(5)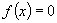 的解集如何?
的解集如何?
师生一起归纳得出:
(1)正弦函数、余弦函数的定义域都是 .
.
(2)正弦函数、余弦函数的值域都是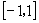 即
即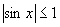 ,
,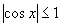 ,称为正弦函数、余弦函数的有界性.
,称为正弦函数、余弦函数的有界性.
(3)取最大值、最小值情况:
正弦函数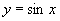 ,当
,当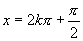 时,(
时,( )函数值
)函数值 取最大值1,当
取最大值1,当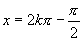 时,(
时,( )函数值
)函数值 取最小值-1.
取最小值-1.
余弦函数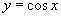 ,当
,当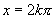 ,(
,( )时,函数值
)时,函数值 取最大值1,当
取最大值1,当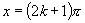 ,(
,( )时,函数值
)时,函数值 取最小值-1.
取最小值-1.
(4)正负值区间: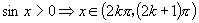
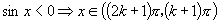
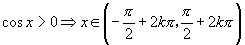
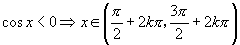 (
( )
)
(5)零点: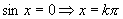 (
( )
)
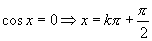 (
( )
)
3.例题分析
[例1]求下列函数的定义域、值域:
(1)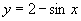 ; (2)
; (2)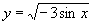 ; (3)
; (3)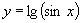 .
.
解:(1) ,
,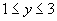
(2)由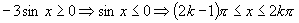 (
( )
)
又∵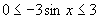 ,∴
,∴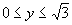
∴定义域为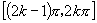 (
( ),值域为
),值域为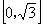 .
.
(3)由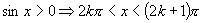 (
( ),又由
),又由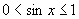
∴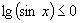
∴定义域为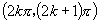 (
( ),值域为
),值域为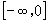 .
.
指出:求值域应注意用到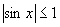 或
或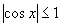 有界性的条件.
有界性的条件.
[例2]求下列函数的最大值,并求出最大值时 的集合:
的集合:
(1)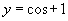 ,
, ; (2)
; (2)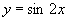 ,
, ;
;
(3)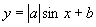 (4)
(4)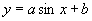 .
.
解:(1)当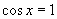 ,即
,即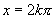 (
( )时,
)时, 取得最大值
取得最大值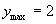
∴函数的最大值为2,取最大值时 的集合为
的集合为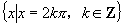 .
.
(2)当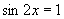 时,即
时,即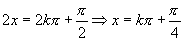 (
( )时,
)时, 取得最大值
取得最大值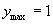 .
.
∴函数的最大值为1,取最大值时 的集合为
的集合为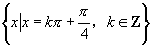 .
.
(3)若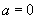 ,
,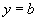 ,此时函数为常数函数.
,此时函数为常数函数.
若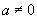 时,
时, ∴
∴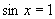 时,即
时,即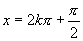 (
( )时,函数取最大值
)时,函数取最大值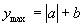 ,
,
∴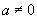 时函数的最大值为
时函数的最大值为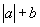 ,取最大值时
,取最大值时 的集合为
的集合为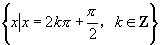 .
.
(4)若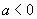 ,则当
,则当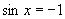 时,函数取得最大值
时,函数取得最大值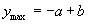 .
.
若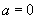 ,则
,则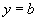 ,此时函数为常数函数.
,此时函数为常数函数.
若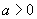 ,当
,当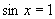 时,函数取得最大值
时,函数取得最大值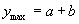 .
.
∴当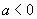 时,函数取得最大值
时,函数取得最大值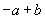 ,取得最大值时
,取得最大值时 的集合为
的集合为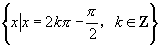 ;当
;当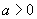 时,函数取得最大值
时,函数取得最大值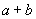 ,取得最大值时
,取得最大值时 的集合为
的集合为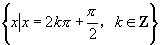 ,当
,当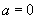 时,函数无最大值.
时,函数无最大值.
指出:对于含参数的最大值或最小值问题,要对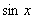 或
或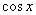 的系数进行讨论.
的系数进行讨论.
思考:此例若改为求最小值,结果如何?
[例3]要使下列各式有意义应满足什么条件?
(1)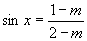 ; (2)
; (2)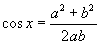 .
.
解:(1)由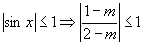 ,
,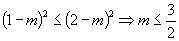
∴当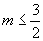 时,式子有意义.
时,式子有意义.
(2)由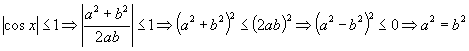 ,即
,即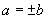
∴当 时,式子有意义.
时,式子有意义.
4.演练反馈(投影)
(1)函数 ,
,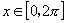 的简图是( )
的简图是( )
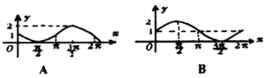
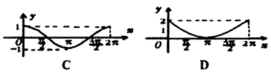
(2)函数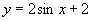 的最大值和最小值分别为( )
的最大值和最小值分别为( )
A.2,-2 B.4,0 C.2,0 D.4,-4
(3)函数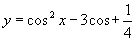 的最小值是( )
的最小值是( )
A.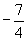 B.-2
C.
B.-2
C.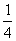 D.
D.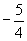
(4)如果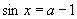 与
与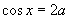 同时有意义,则
同时有意义,则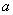 的取值范围应为( )
的取值范围应为( )
A.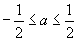 B.
B.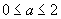 C.
C.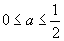 D.
D.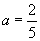 或
或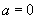
(5)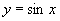 与
与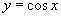 都是增函数的区间是( )
都是增函数的区间是( )
A.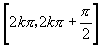 ,
, B.
B.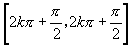 ,
,
C.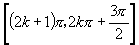 ,
, D.
D.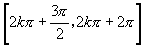 ,
,
(6)函数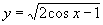 的定义域________,值域________,
的定义域________,值域________,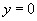 时
时 的集合为_________.
的集合为_________.
参考答案:1.B 2.B 3.A 4.C 5.D
6.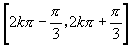
 ;
;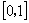 ;
;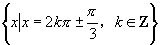
5.总结提炼
(1)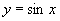 ,
,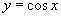 的定义域均为
的定义域均为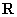 .
.
(2) 、
、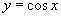 的值域都是
的值域都是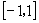
(3)有界性: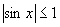
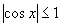
(4)最大值或最小值都存在,且取得极值的 集合为无限集.
集合为无限集.
(5)正负敬意及零点,从图上一目了然.
(6)单调区间也可以从图上看出.
(二)教学目标
1.掌握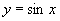 ,
,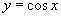 的定义域、值域、最值、单调区间.
的定义域、值域、最值、单调区间.
2.会求含有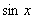 、
、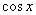 的三角式的定义域.
的三角式的定义域.
(一)教学具准备
直尺,投影仪.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com