
在平面内取定一点O,O点叫作极点:从O起引一条射线O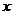 ,这条从极点起的射线O
,这条从极点起的射线O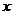 叫作极轴;选定长度单位,再选定角度的下方向(逆时针转角为正向),这种取定了极点、极轴、长度单位与角度正向的坐标系叫作极坐标系。
叫作极轴;选定长度单位,再选定角度的下方向(逆时针转角为正向),这种取定了极点、极轴、长度单位与角度正向的坐标系叫作极坐标系。
对于平面上的一个点M,连接极点O与M,线段OM之长 叫作M点的极径(或矢径、或向径),极轴O
叫作M点的极径(或矢径、或向径),极轴O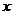 为始边按逆时针转到OM的角
为始边按逆时针转到OM的角 叫作M点的极角,有序数对(
叫作M点的极角,有序数对( ,
, )叫作M点的极坐标。
)叫作M点的极坐标。
当M在极点时,它的极径 =0,极角
=0,极角 可取任何实数。
可取任何实数。
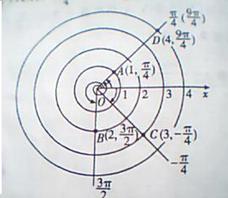
在极坐标系中,若无特殊声明, 是非负实数,
是非负实数,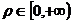 ,
,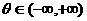 。
。
 当
当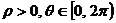 时,平面上的点与极坐标一一对应。事实上,对给定的
时,平面上的点与极坐标一一对应。事实上,对给定的 与
与 ,由极坐标(
,由极坐标( ,
, )可以唯一地确定一个点M,但是反过来,平面上给定一点,却可以写出这个点的无数多个极坐标。根据点的极坐标(
)可以唯一地确定一个点M,但是反过来,平面上给定一点,却可以写出这个点的无数多个极坐标。根据点的极坐标( ,
, )的定义,对于给定的点,它的极径
)的定义,对于给定的点,它的极径 是唯一确定的,但极角却可以有无穷多种,如果我们写出了它的极坐标(
是唯一确定的,但极角却可以有无穷多种,如果我们写出了它的极坐标( ,
, ),则(
),则( ,
,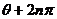 )也是这个点的极坐标,其中
)也是这个点的极坐标,其中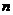 是任意整数,当
是任意整数,当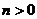 时,
时,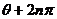 表示从该点起绕极点O逆时针转动了
表示从该点起绕极点O逆时针转动了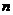 圈又回到原处,当
圈又回到原处,当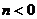 时,
时,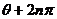 表示从该点起绕极点O顺时针转动了
表示从该点起绕极点O顺时针转动了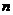 圈又回到原处。
圈又回到原处。
直角坐标系是最常用的坐标系,但它不是用数来刻画点的位置的唯一方法,用哪种方法最方便,要对具体问题作具体分析。
如力所示,缉私观测站位于点O处,看到们于点A处的走私船正在逃跑,现停泊于点O处的缉私船追击走私船,随时需要观测站提供走私船所在的位置P。对船舶来说,最方便的数据不是走私船所在点的直角坐标(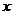 ,
,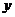 ),而是它的方位角,即夹角
),而是它的方位角,即夹角 。在航空和航海中的情况都是这样。
。在航空和航海中的情况都是这样。
当用炮兵指挥仪指示射击目标时,输出的是目标方位,即方向和距离。在日常生活中,我们也经常用距离和角度指示位置。用距离和方向刻画点的位置,这是建立极坐标系的基本思路。
体会在极坐标系和平面直角坐标系中刻画点的位置的区别;
教学重点: 极坐标( ,
, )与平面上的点的关系
)与平面上的点的关系
教学难点:极坐标( ,
, )与平面上的点的关系;
)与平面上的点的关系;
教学过程
借助生活中的实例引入极坐标的概念;比较点在极坐标系和平面直角坐标系中的坐标关系
知道在极坐标系中刻画点的位置的方法;
(1)下列说法正确的是( ).
 奇函数的图象一定过原点
奇函数的图象一定过原点
 偶函数的图象一定与
偶函数的图象一定与
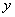 轴相交
轴相交
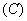
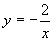 在其定义域内是增函数
在其定义域内是增函数
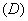
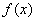 是奇函数的充要条件是它的图象关于原点对称
是奇函数的充要条件是它的图象关于原点对称
(2)下列函数中,在区间 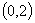 上为增函数的是( ).
上为增函数的是( ).
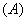
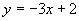
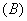

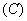
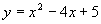
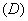
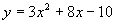
(3)函数 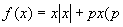 为常数),则( )
为常数),则( )
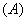 对任何常数
对任何常数
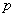 ,
, 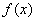 是既不是奇函数也不是偶函数
是既不是奇函数也不是偶函数
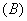 对任何常数
对任何常数
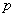 ,
, 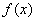 是奇函数
是奇函数
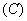 对任何常数
对任何常数
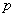 ,
, 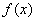 是偶函数
是偶函数
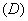 只有当
只有当
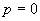 时,
时, 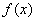 是奇函数
是奇函数
2. 若函数 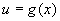 在区间
在区间
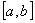 上是单调函数,函数
上是单调函数,函数 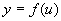 在
在
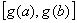 或
或
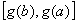 上也是单调函数,那么复合函数
上也是单调函数,那么复合函数 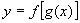 在区间
在区间
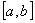 上是单调函数,其单调性规律是:
上是单调函数,其单调性规律是:
|
函数 |
单调性 |
|||
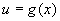 |
增函数 |
增函数 |
减函数 |
减函数 |
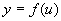 |
增函数 |
减函数 |
增函数 |
减函数 |
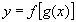 |
增函数 |
减函数 |
减函数 |
增函数 |
即 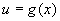 ,
, 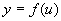 增减性相同时,
增减性相同时, 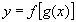 为增函数,增减性相反时,
为增函数,增减性相反时, 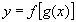 为减函数.
为减函数.
选自《名师一点通高中代数》
辽宁教育出版社 蒋佩锦编著
探究活动
(1)
定义域为 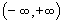 的任意函数
的任意函数
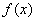 都可以表示成一个奇函数和一个偶函数的和,你能试证明之吗?
都可以表示成一个奇函数和一个偶函数的和,你能试证明之吗?
(2) 判断函数 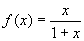 在
在
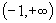 上的单调性,并加以证明.
上的单调性,并加以证明.
在此基础上试利用这个函数的单调性解决下面的问题:
设 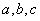 为三角形的三条边,求证:
为三角形的三条边,求证: 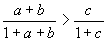 .
.
习题精选
|
2.函数的奇偶性 例1.
例3. (1) 偶函数定义 (2) 奇函数定义 (3) 定义域关于原点对称是函数 例2. 小结 具备奇偶性的必要条件 (4)函数按奇偶性分类分四类 |
扩展资料
复合函数的单调性与奇偶性
复合函数的性质与构成它的函数的性质密切相关,其规律可列表如下:
1.若函数 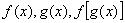 的定义域都是关于原点对称的,那么由
的定义域都是关于原点对称的,那么由 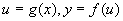 的奇偶性得到
的奇偶性得到
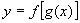 的奇偶性的规律是:
的奇偶性的规律是:
|
函数 |
奇偶性 |
|||
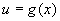 |
奇函数 |
奇函数 |
偶函数 |
偶函数 |
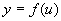 |
奇函数 |
偶函数 |
奇函数 |
偶函数 |
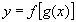 |
奇函数 |
偶函数 |
偶函数 |
偶函数 |
即当且仅当 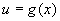 和
和
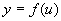 都是奇函数时,复合函数
都是奇函数时,复合函数 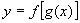 是奇函数.
是奇函数.
2. 判断中注意的问题
1. 奇偶性的概念
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com