
课本24页 习题7,8,9,10,11,12
教学反思:
平面直角坐标系与极坐标系中同一点的直角坐标(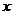 ,
,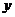 )与其极坐标(
)与其极坐标( ,
, )之间的换算公式。
)之间的换算公式。
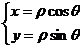
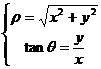
4、把极坐标方程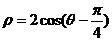 化为直角坐标方程
化为直角坐标方程
3、写出圆心在点(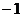 ,1),且过原点的圆的直角坐标方程,并把它化为极坐标方程。
,1),且过原点的圆的直角坐标方程,并把它化为极坐标方程。
2、把点A的直角坐标(1,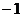 )化为极坐标。
)化为极坐标。
1、把点M的极坐标(3,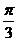 )化为直角坐标;
)化为直角坐标;
例1、在平面直角坐标系中,把曲线的方程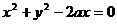 化为极坐标系中的方程。
化为极坐标系中的方程。
解:把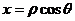 ,
,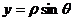 代入方程
代入方程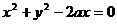 得
得
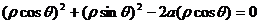
 即
即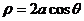
此方程我们在上节课得出过,它是圆心在极轴上,半径为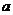 ,过极点的圆的极坐标方程。事实上
,过极点的圆的极坐标方程。事实上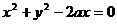 恰为圆心在(
恰为圆心在(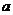 ,0),半径为
,0),半径为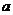 的圆
的圆
例2、已知曲线的极坐标方程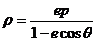 ,求此曲线的直角坐标方程,其中
,求此曲线的直角坐标方程,其中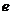 与
与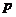 是正常数。
是正常数。
解:方程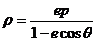 写成
写成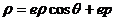
把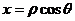 与
与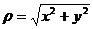 代入得
代入得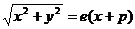
两端平方化简得: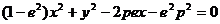
当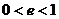 时,方程表示一个椭圆
时,方程表示一个椭圆
当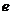 =1时,方程表示一条抛物线
=1时,方程表示一条抛物线
当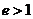 时,方程表示双曲线
时,方程表示双曲线
极坐标方程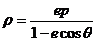 是椭圆、抛物线、双曲线这三种圆锥曲线的统一的极坐标方程。
是椭圆、抛物线、双曲线这三种圆锥曲线的统一的极坐标方程。
在平面上的同一个点,它的平面直角坐标(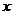 ,
,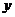 )与极坐标(
)与极坐标( ,
, )之间有什么样的换算公式?同一条曲线,它在平面直角坐标系中的方程为
)之间有什么样的换算公式?同一条曲线,它在平面直角坐标系中的方程为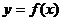 或
或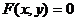 ,在极坐标系中的方程为
,在极坐标系中的方程为 或
或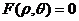 ,如果知道其中它的一种方程,如何换算出另一种方程呢?
,如果知道其中它的一种方程,如何换算出另一种方程呢?
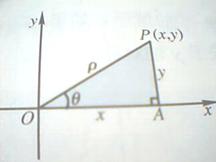 我们把极轴与平面直角坐标系
我们把极轴与平面直角坐标系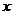 O
O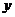 的
的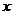 正半轴重合,且两种坐标系取相同的长度单位,设
正半轴重合,且两种坐标系取相同的长度单位,设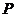 (
(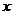 ,
,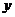 )是平面上的任意一点,如图,则
)是平面上的任意一点,如图,则
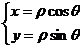 (1)
(1)
由(1)式可得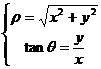 (2)
(2)
(1)与(2)是平面直角坐标系与极坐标系中同一点的直角坐标(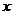 ,
,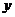 )与其极坐标(
)与其极坐标( ,
, )之间的换算公式。
)之间的换算公式。
3、几类特殊曲线的极坐标方程
①过极点直线的极坐标方程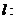

②过已知点A(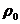 ,
,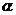 )且平行于极轴的直线的极坐标方程:
)且平行于极轴的直线的极坐标方程:
③过已知点A(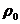 ,
,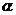 )且垂直于极轴的直线的极坐标方程:
)且垂直于极轴的直线的极坐标方程: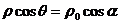
④过点A(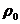 ,
,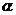 )且和极轴成
)且和极轴成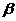 角的直线的极坐标方程:
角的直线的极坐标方程: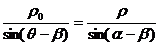
⑤极点O到直线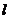 的距离为
的距离为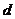 ,由点O向直线
,由点O向直线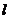 作垂线OA,由极轴到垂线OA的角度为
作垂线OA,由极轴到垂线OA的角度为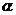 的直线
的直线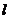 的极坐标方程:
的极坐标方程: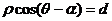
⑥圆心在极点的圆的极坐标方程: =
=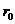
⑦圆心在极轴,过极点的圆的极坐标方程 =2
=2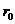
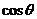
⑧以(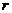 ,
,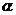 )为圆心,以
)为圆心,以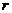 为半径的圆(即圆过极点)极坐标方程
为半径的圆(即圆过极点)极坐标方程 =2
=2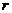
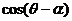
⑨阿基米德螺线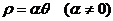
2、对于平面上的一个点M,连接极点O与M,线段OM之长 叫作M点的极径(或矢径、或向径),极轴O
叫作M点的极径(或矢径、或向径),极轴O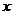 为始边按逆时针转到OM的角
为始边按逆时针转到OM的角 叫作M点的极角,有序数对(
叫作M点的极角,有序数对( ,
, )叫作M点的极坐标。
)叫作M点的极坐标。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com