
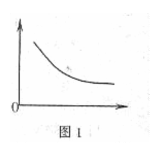
3.下列关于稳态的调节,符合图1曲线走势的是
A.若横轴代表血糖浓度,则纵轴可以代表胰岛素浓度
B.若横轴代表甲状腺激素浓度,则纵轴可以代表促
甲状腺激素浓度 ( B )
( B )
C.若横轴代表注射疫苗后的时间,则纵轴可以代表
短时间内相应抗体的浓度
D.若横轴代表生态系统的生物种类,则纵轴可以代表
该生态系 统的抵抗力稳定性
统的抵抗力稳定性
[解析]图中横坐标和纵坐标为相反的变化关系。血糖浓度越高,胰岛素越高;注射疫苗抗体会有先增加后减少的变化;生态系统的生物种类越多,生态系统的抵抗力稳定性越高。
2.癌症是威胁人类健康的一类重要疾病,为攻克癌症,人们对它进行了大量研究,以下有关叙述正确的是: ( D )
A.同一个体的癌细胞与正常细胞遗传物质相同
B.细胞癌变使人体自身的细胞成为抗原,能使其裂解死亡的免疫细胞是效应B细胞
C.用单克隆抗体制成“生物导弹”来治疗癌症,在临床上已被广泛应用
D.癌细胞的细胞周期变短,线粒体和核糖体的活动增强
 [解析]“生物导弹”来治疗癌症,将有广阔的应用前景,还没有被广泛应用;癌细胞是无限增殖的细胞,细胞周期变短,蛋白质合成旺盛。
[解析]“生物导弹”来治疗癌症,将有广阔的应用前景,还没有被广泛应用;癌细胞是无限增殖的细胞,细胞周期变短,蛋白质合成旺盛。
1.洋葱根尖分生区细胞在分裂过程中不会出现的是 ( A )
A.在细胞周期的分裂期,核糖体上合成DNA聚合酶和RNA聚合酶
B.在细胞分裂前期,细胞两极发出纺锤丝形成纺缍体
C.在细胞分裂中期,细胞内ATP的含量减少
D.在细胞分裂末期,高尔基体与细胞壁的形成有关
[解析]核糖体上合成DNA聚合酶和RNA聚合酶在分裂间期。
21.(本小题满分13分)
设数列 的前
的前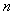 项和为
项和为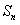 ,已知
,已知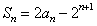 (n∈N*).
(n∈N*).
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列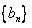 的前
的前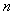 项和为
项和为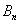 ,若存在整数
,若存在整数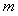 ,使对任意n∈N*且n≥2,都有
,使对任意n∈N*且n≥2,都有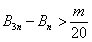 成立,求
成立,求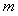 的最大值;
的最大值;
(Ⅲ)令 ,
, 数列
数列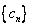 的前
的前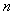 项和为
项和为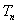 ,求证:当n∈N*且n≥2时,
,求证:当n∈N*且n≥2时,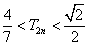 .
.
[解](Ⅰ)由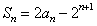 ,得
,得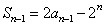 (n≥2).
(n≥2).
两式相减,得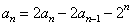 ,即
,即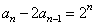 (n≥2).
(1分)
(n≥2).
(1分)
于是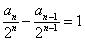 ,所以数列
,所以数列 是公差为1的等差数列.
(2分)
是公差为1的等差数列.
(2分)
又 ,所以
,所以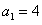 .
(3分)
.
(3分)
所以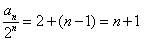 ,故
,故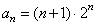 .
(4分)
.
(4分)
(Ⅱ)因为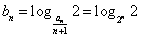
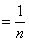 ,则
,则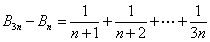 . (5分)
. (5分)
令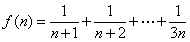 ,则
,则
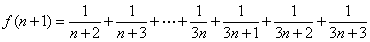 .
.
所以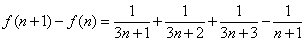
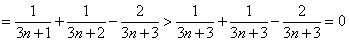 .
.
即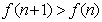 ,所以数列
,所以数列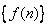 为递增数列.
(7分)
为递增数列.
(7分)
所以当n≥2时,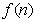 的最小值为
的最小值为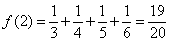 .
.
据题意,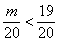 ,即
,即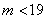 .又
.又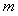 为整数,故
为整数,故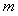 的最大值为18.
(8分)
的最大值为18.
(8分)
(Ⅲ)因为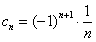 ,则当n≥2时,
,则当n≥2时,
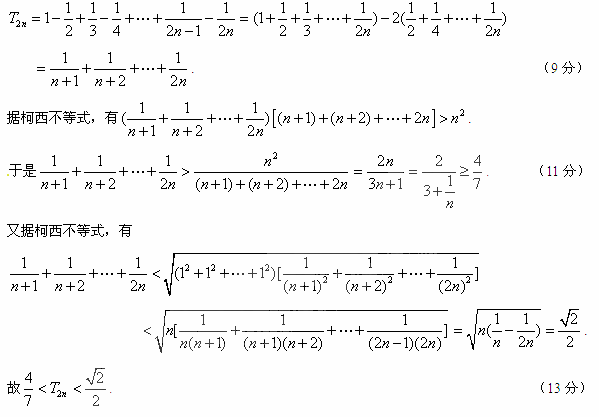
20.(本小题满分13分)
设向量a=(x+1,y),b=(x-1,y),点P(x,y)为动点,已知|a|+|b|=4.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P的轨迹与x轴负半轴交于点A,过点F(1,0)的直线交点P的轨迹于B、C两点,试推断△ABC的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由.
[解](Ⅰ)由已知,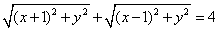 (1分)
(1分)
所以动点P的轨迹M是以点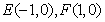 为焦点,长轴长为4的椭圆.
(3分)
为焦点,长轴长为4的椭圆.
(3分)
因为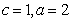 ,则
,则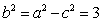 .
(4分)
.
(4分)
故动点P的轨迹M的方程是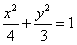 .
(5分)
.
(5分)
(Ⅱ)设直线BC的方程为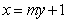 ,
,
由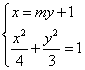
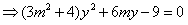 .
(6分)
.
(6分)
设点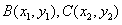 ,则
,则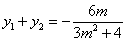 ,
,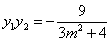 .
(7分)
.
(7分)
所以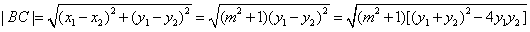
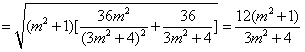 .
(8分)
.
(8分)
由题设,点A的坐标是(-2,0),则点A到直线BC的距离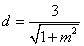 .
(9分)
.
(9分)
所以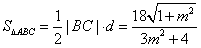 .
.
令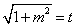 ,则
,则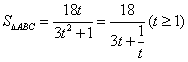 .
(10分)
.
(10分)
设 ,则
,则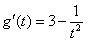 .因为当
.因为当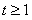 时,
时,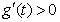 ,则函数
,则函数 在
在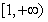 上是增函数.
(11分)
上是增函数.
(11分)
所以当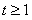 时,
时,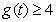 ,从而
,从而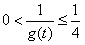 ,所以
,所以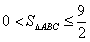 .
(12分)
.
(12分)
故△ABC的面积存在最大值,其最大值为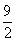 .
(13分)
.
(13分)
19.(本小题满分13分)
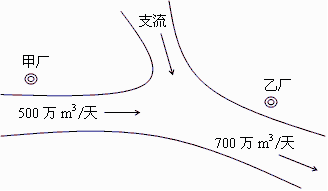
如图,某化工集团在一条河流的上、下游分别建有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放. 根据环保部门的要求,整个河流中污水含量不能超过0.2%,为此,甲、乙两个工厂都必须各自处理一部分污水.
(Ⅰ)设甲、乙两个化工厂每天各自处理的污水分别为x、y万m3,试根据环保部门的要求写出x、y所满足的所有条件;
(Ⅱ)已知甲厂处理污水的成本是1200元/万m3,乙厂处理污水的成本是1000元/万m3,在满足环保部门要求的条件下,甲、乙两个化工厂每天应分别各自处理污水多少万m3,才能使这两个工厂处理污水的总费用最小?最小总费用是多少元?
、
[解](Ⅰ)据题意,x、y所满足的所有条件是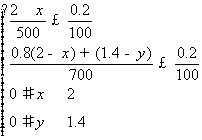 ,
,
(4分)
即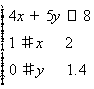 .
.
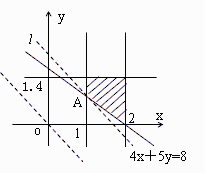
 (6分)
(6分)
(Ⅱ)设甲、乙两厂处理污水的总费用为z元,则
目标函数z=1200x+1000y=200(6x+5y). (7分)
作可行域,如图. (10分)
平移直线l:6x+5y=0,当直线经过点A(1,0.8)时,、
z取最大值,此时z=1200×1+1000×0.8=2000(元).  (12分)
(12分)
故甲、乙两厂每天应分别处理1万m3、0.8万m3污水,
才能使两厂处理污水的总费用最小,且最小总费用是2000元. (13分)
18.(本小题满分12分)
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,点F在CE上,且BF⊥平面ACE.
(Ⅰ)判断平面ADE与平面BCE是否垂直,并说明理由;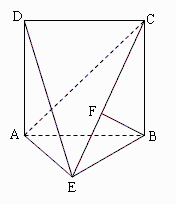
(Ⅱ)求点D到平面ACE的距离.
[解](Ⅰ)因为BF⊥平面ACE,所以BF⊥AE. (2分)
因为平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB,所以BC⊥平面ABE,
从而BC⊥AE. (5分)
于是AE⊥平面BCE,故平面ADE⊥平面BCE. (6分)
(Ⅱ)方法一:连结BD交AC与点M,则点M是BD的中点,
所以点D与点B到平面ACE的距离相等.
因为BF⊥平面ACE,所以BF为点B到平面ACE的距离.
 (8分)、
(8分)、
因为AE⊥平面BCE,所以AE⊥BE.、
又AE=BE,所以△AEB是等腰直角三角形.
因为AB=2,所以BE=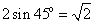 .
(9分)
.
(9分)
在Rt△CBE中,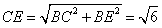 .
(10分)
.
(10分)
所以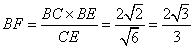 .
.
故点D到平面ACE的距离是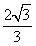 .
(12分)
.
(12分)
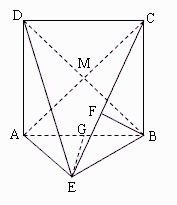
方法二:过点E作EG⊥AB,垂足为G,因为平面ABCD⊥平面ABE,所以EG⊥平面ABCD.
因为 AE⊥平面BCE,所以AE⊥BE.又AE=BE,所以△AEB是等腰直角三角形,从而G为AB的中点.又AB=2,所以EG=1.
(8分)
AE⊥平面BCE,所以AE⊥BE.又AE=BE,所以△AEB是等腰直角三角形,从而G为AB的中点.又AB=2,所以EG=1.
(8分)
因为AE⊥平面BCE ,所以AE⊥EC.
又AE=BE=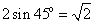 ,
,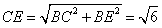 .
(10分)
.
(10分)
设点D到平面ACE的距离为h,因为VD-ACE=VE-ACD,则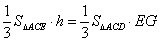 .
.
所以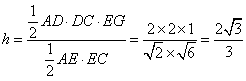 ,故点D到平面ACE的距离是
,故点D到平面ACE的距离是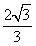 . (12分)
. (12分)
17.(本小题满分12分)
甲、乙两名射击运动员进行射击选拔比赛,已知甲、乙两运动员射击的环数稳定在6,7,8,9,10环,其射击比赛成绩的分布列如下:
甲运动员:
|
ξ |
6 |
7 |
8、 |
9 |
10 |
|
P |
0.16 |
0.14 |
0.42 |
0.1 |
0.18 |
乙运动员:、
|
η |
6 |
7 |
8 |
9 |
10 |
|
P |
0.19 |
0.24 |
0.12、 |
0.28 |
0.17 |
(Ⅰ)若甲、乙两运动员各射击一次,求同时击中9环以上(含9环)的概率;
(Ⅱ)若从甲、乙两运动员中只能挑选一名参加某项国际比赛,你认为让谁参加比赛较合适?并说明理由.
[解](Ⅰ)记“甲运动员击中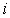 环”为事件
环”为事件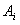 ;“乙运动员击中
;“乙运动员击中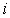 环”为事件
环”为事件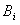 ;“甲、乙两运动员同时击中9环(含9环)”为事件C.
(2分)
;“甲、乙两运动员同时击中9环(含9环)”为事件C.
(2分)
因为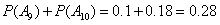 ,
,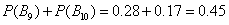 . (4分)
. (4分)
所以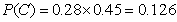 .
.
故甲、乙两运动员同时击中9环以上(含9环)的概率为0.126.  (6分)
(6分)
(Ⅱ)由分布列可知,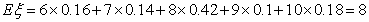 . (7分)
. (7分)
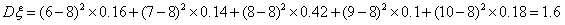 .
.
(8分)
又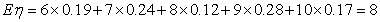 .
(9分)
.
(9分)
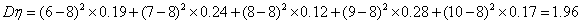
(10分)
因为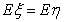 ,
,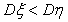 ,所以甲、乙两运动员射击成绩的均值相等,但甲射击成绩的稳定性比乙要好,故选派甲参加比赛
,所以甲、乙两运动员射击成绩的均值相等,但甲射击成绩的稳定性比乙要好,故选派甲参加比赛 较合适.
(12分)
较合适.
(12分)
16.(本小题满分12分)
设角A,B,C为△ABC的三个内角.
(Ⅰ)若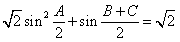 ,求角A的大小;
,求角A的大小;
(Ⅱ)设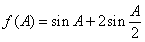 ,求当A为何值时,f(A)取极大值,并求其极大值.
,求当A为何值时,f(A)取极大值,并求其极大值.
[解析](Ⅰ)由已知,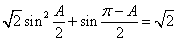 ,即
,即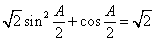 . (2分)
. (2分)
所以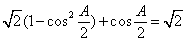 ,即
,即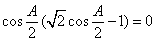 .
(4分)
.
(4分)
在△ABC中,因为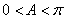 ,则
,则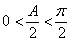 ,所以
,所以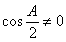 ,从而
,从而 . (5分)
. (5分)
而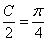 ,即
,即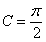 .
(6分)
.
(6分)
(Ⅱ)因为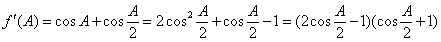 . (8分)
. (8分)
因为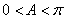 ,则
,则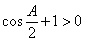 .由
.由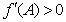 ,得
,得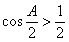 ,所以
,所以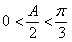 ,即
,即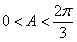 .、
.、
所以当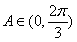 时,
时,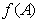 为增函数;当
为增函数;当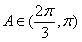 时,
时,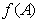 为减函数.
(10分)
为减函数.
(10分)
故当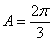 时,
时,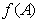 取极大值,且极大值为
取极大值,且极大值为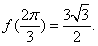 (12分)
(12分)
15.设a,b,λ都为正数,且a≠b,对于函数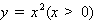 图象上两点
图象上两点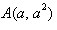 ,
,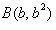 .
.
(1)若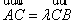 ,则点C的坐标是
,则点C的坐标是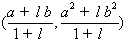 ;
;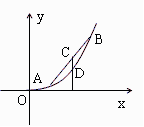
(2)过点C作x轴的垂线,交函数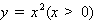 的图象于D点,
的图象于D点,
由点C在点D的上方可得不等式: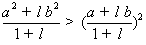 .
.
[解析](1)设点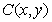 ,因为点
,因为点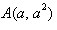 ,
,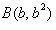 ,
,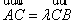 ,则
,则
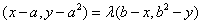 ,所以
,所以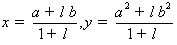 .
.
(2)因为点C在点D的上方,则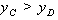 ,所以
,所以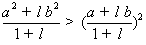 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com