2.能利用数量积的5个重要性质及数量积运算规律解决有关问题；

教学目的：

1.掌握平面向量数量积运算规律；

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (王海)

第8课时

9.对于两个非零向量a、b，求使|a+tb|最小时的t值，并求此时b与a+tb的夹角.

8.设m、n是两个单位向量，其夹角为60°，求向量a=2m+n与b=2n-3m的夹角.

7.已知|a|=1，|b|=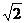，(1)若a∥b，求a·b；(2)若a、b的夹角为60°，求|a+b|；(3)若a-b与a垂直，求a与b的夹角.

6.已知a⊥b、c与a、b的夹角均为60°，且|a|=1，|b|=2，|c|=3，则(a+2b-c)²＝______.

5.已知a+b=2i-8j，a-b=-8i+16j，其中i、j是直角坐标系中x轴、y轴正方向上的单位向量，那么a·b=　　　　　 .

4.已知向量a、b的夹角为，|a|=2，|b|=1，则|a+b|·|a-b|=　　　　　　 .

3.已知a、b是非零向量，则|a|=|b|是(a+b)与(a-b)垂直的(　　 )

A.充分但不必要条件　　　　　　　 B.必要但不充分条件　

C.充要条件　　　　　　　　　　　 D.既不充分也不必要条件