
2.掌握平面向量数量积的重要性质及运算律;
教学目的:
1.掌握平面向量的数量积及其几何意义;
(王海)
§2.4平面向量的数量积
第7课时
6.已知□ABCD四个顶点的坐标为A(5,7),B(3,x),C(2,3),D(4,x),则x= .
5.已知a=(1,2),b=(x,1),若a+2b与2a-b平行,则x的值为 .
4.已知a=(4,2),b=(6,y),且a∥b,则y= .
3.若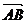 =i+2j,
=i+2j, 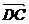 =(3-x)i+(4-y)j(其中i、j的方向分别与x、y轴正方向相同且为单位向量).
=(3-x)i+(4-y)j(其中i、j的方向分别与x、y轴正方向相同且为单位向量). 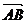 与
与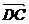 共线,则x、y的值可能分别为( )
共线,则x、y的值可能分别为( )
A.1,2 B.2,2 C.3,2 D.2,4
2.若A(x,-1),B(1,3),C(2,5)三点共线,则x的值为( )
A.-3 B.-1 C.1 D.3
1.若a=(2,3),b=(4,-1+y),且a∥b,则y=( )
A.6 B.5 C.7 D.8
例1已知 =(4,2),
=(4,2),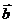 =(6,
y),且
=(6,
y),且 ∥
∥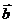 ,求y.
,求y.
例2已知A(-1, -1), B(1,3), C(2,5),试判断A,B,C三点之间的位置关系.
例3设点P是线段P1P2上的一点, P1、P2的坐标分别是(x1,y1),(x2,y2).
(1) 当点P是线段P1P2的中点时,求点P的坐标;
(2) 当点P是线段P1P2的一个三等分点时,求点P的坐标.
例4若向量 =(-1,x)与
=(-1,x)与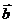 =(-x,
2)共线且方向相同,求x
=(-x,
2)共线且方向相同,求x
解:∵ =(-1,x)与
=(-1,x)与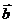 =(-x,
2) 共线 ∴(-1)×2-
x•(-x)=0
=(-x,
2) 共线 ∴(-1)×2-
x•(-x)=0
∴x=±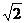 ∵
∵ 与
与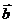 方向相同 ∴x=
方向相同 ∴x=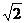
例5 已知A(-1,
-1), B(1,3), C(1,5)
,D(2,7) ,向量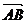 与
与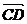 平行吗?直线AB与平行于直线CD吗?
平行吗?直线AB与平行于直线CD吗?
解:∵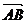 =(1-(-1), 3-(-1))=(2,
4) ,
=(1-(-1), 3-(-1))=(2,
4) , 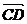 =(2-1,7-5)=(1,2)
=(2-1,7-5)=(1,2)
又 ∵2×2-4×1=0 ∴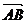 ∥
∥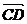
又 ∵ 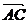 =(1-(-1), 5-(-1))=(2,6) ,
=(1-(-1), 5-(-1))=(2,6) ,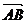 =(2,
4),2×4-2×6¹0 ∴
=(2,
4),2×4-2×6¹0 ∴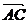 与
与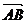 不平行
不平行
∴A,B,C不共线 ∴AB与CD不重合 ∴AB∥CD
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com