问题1：弄清求变力做功的几种方法

功的计算在中学物理中占有十分重要的地位，中学阶段所学的功的计算公式W=FScosa只能用于恒力做功情况，对于变力做功的计算则没有一个固定公式可用，下面对变力做功问题进行归纳总结如下：

1、等值法

　等值法即若某一变力的功和某一恒力的功相等，则可以通过计算该恒力的功，求出该变力的功。而恒力做功又可以用W=FScosa计算，从而使问题变得简单。

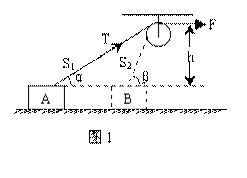
　例1、如图1，定滑轮至滑块的高度为h，已知细绳的拉力为F(恒定)，滑块沿水平面由A点前进S至B点，滑块在初、末位置时细绳与水平方向夹角分别为α和β。求滑块由A点运动到B点过程中，绳的拉力对滑块所做的功。

分析与解：设绳对物体的拉力为T，显然人对绳的拉力F等于T。T在对物体做功的过程中大小虽然不变，但其方向时刻在改变，因此该问题是变力做功的问题。但是在滑轮的质量以及滑轮与绳间的摩擦不计的情况下，人对绳做的功就等于绳的拉力对物体做的功。而拉力F的大小和方向都不变，所以F做的功可以用公式W=FScosa直接计算。由图1可知，在绳与水平面的夹角由α变到β的过程中,拉力F的作用点的位移大小为：　

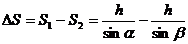
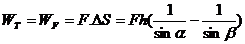
5.深刻理解功能关系，掌握能量守恒定律。

(1)做功的过程是能量转化的过程，功是能的转化的量度。

　　 能量守恒和转化定律是自然界最基本的规律之一。而在不同形式的能量发生相互转化的过程中，功扮演着重要的角色。本章的主要定理、定律都可由这个基本原理出发而得到。

需要强调的是：功是一个过程量，它和一段位移(一段时间)相对应；而能是一个状态量，它与一个时刻相对应。两者的单位是相同的(都是J)，但不能说功就是能，也不能说“功变成了能”。

　　 (2)复习本章时的一个重要课题是要研究功和能的关系，尤其是功和机械能的关系。突出：“功是能量转化的量度”这一基本概念。

1物体动能的增量由外力做的总功来量度：W_外=ΔE_k，这就是动能定理。

2物体重力势能的增量由重力做的功来量度：W_G= -ΔE_P，这就是势能定理。

3物体机械能的增量由重力以外的其他力做的功来量度：W_其=ΔE_机，(W_其表示除重力以外的其它力做的功)，这就是机械能定理。

4当W_其=0时，说明只有重力做功，所以系统的机械能守恒。

5一对互为作用力反作用力的摩擦力做的总功，用来量度该过程系统由于摩擦而减小的机械能，也就是系统增加的内能。Q=fd(d为这两个物体间相对移动的路程)。

2.机械能守恒定律的各种表达形式

⑴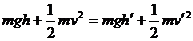，即；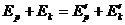

⑵；；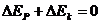

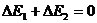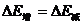
　　 用⑴时，需要规定重力势能的参考平面。用⑵时则不必规定重力势能的参考平面，因为重力势能的改变量与参考平面的选取没有关系。尤其是用ΔE_增=ΔE_减，只要把增加的机械能和减少的机械能都写出来，方程自然就列出来了。

1.机械能守恒定律的两种表述

⑴在只有重力做功的情形下，物体的动能和重力势能发生相互转化，但机械能的总量保持不变。

⑵如果没有摩擦和介质阻力，物体只发生动能和重力势能的相互转化时，机械能的总量保持不变。

　　 对机械能守恒定律的理解：

　　 ①机械能守恒定律的研究对象一定是系统，至少包括地球在内。通常我们说“小球的机械能守恒”其实一定也就包括地球在内，因为重力势能就是小球和地球所共有的。另外小球的动能中所用的v，也是相对于地面的速度。

　　 ②当研究对象(除地球以外)只有一个物体时，往往根据是否“只有重力做功”来判定机械能是否守恒；当研究对象(除地球以外)由多个物体组成时，往往根据是否“没有摩擦和介质阻力”来判定机械能是否守恒。

　　 ③“只有重力做功”不等于“只受重力作用”。在该过程中，物体可以受其它力的作用，只要这些力不做功。

4.深刻理解势能的概念，掌握机械能守恒定律。

3.深刻理解动能的概念，掌握动能定理。

(1) 动能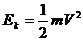是物体运动的状态量，而动能的变化ΔE_K是与物理过程有关的过程量。

(2)动能定理的表述

合外力做的功等于物体动能的变化。(这里的合外力指物体受到的所有外力的合力，包括重力)。表达式为W=ΔE_K.

动能定理也可以表述为：外力对物体做的总功等于物体动能的变化。实际应用时，后一种表述比较好操作。不必求合力，特别是在全过程的各个阶段受力有变化的情况下，只要把各个力在各个阶段所做的功都按照代数和加起来，就可以得到总功。

动能定理建立起过程量(功)和状态量(动能)间的联系。这样，无论求合外力做的功还是求物体动能的变化，就都有了两个可供选择的途径。功和动能都是标量，动能定理表达式是一个标量式，不能在某一个方向上应用动能定理。

2.深刻理解功率的概念

　　 (1)功率的物理意义：功率是描述做功快慢的物理量。

(2)功率的定义式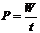：，所求出的功率是时间t内的平均功率。

(3)功率的计算式：P=Fvcosθ，其中θ是力与速度间的夹角。该公式有两种用法：①求某一时刻的瞬时功率。这时F是该时刻的作用力大小，v取瞬时值，对应的P为F在该时刻的瞬时功率；②当v为某段位移(时间)内的平均速度时，则要求这段位移(时间)内F必须为恒力，对应的P为F在该段时间内的平均功率。

(4)重力的功率可表示为P_G=mgV_y，即重力的瞬时功率等于重力和物体在该时刻的竖直分速度之积。

1.深刻理解功的概念

　　 功是力的空间积累效应。它和位移相对应(也和时间相对应)。计算功的方法有两种：

⑴按照定义求功。即：W=Fscosθ。 在高中阶段，这种方法只适用于恒力做功。当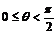时F做正功，当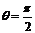时F不做功，当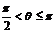时F做负功。

　　 这种方法也可以说成是：功等于恒力和沿该恒力方向上的位移的乘积。

⑵用动能定理W=ΔE_k或功能关系求功。当F为变力时，高中阶段往往考虑用这种方法求功。

　这种方法的依据是：做功的过程就是能量转化的过程，功是能的转化的量度。如果知道某一过程中能量转化的数值，那么也就知道了该过程中对应的功的数值。

(3)．会判断正功、负功或不做功。判断方法有：1用力和位移的夹角α判断;2用力和速度的夹角θ判断定;3用动能变化判断.

　(4)了解常见力做功的特点:

重力做功和路径无关，只与物体始末位置的高度差h有关：W=mgh，当末位置低于初位置时，W＞0，即重力做正功；反之则重力做负功。

滑动摩擦力做功与路径有关。当某物体在一固定平面上运动时，滑动摩擦力做功的绝对值等于摩擦力与路程的乘积。

在弹性范围内，弹簧做功与始末状态弹簧的形变量有关系。

(5)一对作用力和反作用力做功的特点：1一对作用力和反作用力在同一段时间内做的总功可能为正、可能为负、也可能为零；2一对互为作用反作用的摩擦力做的总功可能为零(静摩擦力)、可能为负(滑动摩擦力)，但不可能为正。

15.如图44所示，水平放置的平行金属板A和B的距离为d，它们的右端安放着垂直于金属板的靶MN，现在A、B板上加上如图45所示的方波电压，电压的正向值为U₀，反向电压值为U₀/2，且每隔T/2换向一次，现有质量为m、带正电且电量为q的粒子束从A、B的中点O沿平行于金属板方向OO^/射入，设粒子能全部打在靶上而且所有粒子在A、B间的飞行时间均为T。不计重力的影响，试问：

(1)在靶MN上距其中心O^/点多远的范围内有粒子击中？

(2)要使粒子能全部打在靶MN上，电压U₀的数值应满足什么条件？(写出U₀、m、d、q、T的关系式即可)

14．一质量为m，带电量为+q的小球，用长为L的绝缘线悬挂在水平向右的匀强电场中，开始时把悬线拉到水平，小球在位置A点。然后将小球由静止释放，球沿弧线下摆到α=60⁰的B点(如图43所示)，此时小球速度恰好为零，试求(1)匀强电场场强。(2)小球在运动中的最大速度。