
5. 设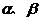 是方程
是方程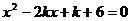 的两个实根,则
的两个实根,则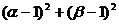 的最小值是
的最小值是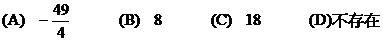
析:误了A,应注意∴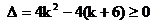 Þ
Þ 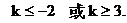
思路分析 本例只有一个答案正确,设了3个陷阱,很容易上当。
利用一元二次方程根与系数的关系易得: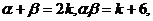
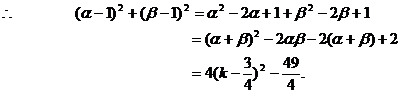
有的学生一看到 ,常受选择答案(A)的诱惑,盲从附和。这正是思维缺乏反思性的体现。如果能以反思性的态度考察各个选择答案的来源和它们之间的区别,就能从中选出正确答案。
,常受选择答案(A)的诱惑,盲从附和。这正是思维缺乏反思性的体现。如果能以反思性的态度考察各个选择答案的来源和它们之间的区别,就能从中选出正确答案。
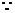 原方程有两个实根
原方程有两个实根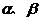 ,∴
,∴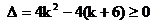 Þ
Þ 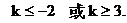
当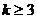 时,
时,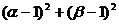 的最小值是8;
的最小值是8;
当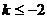 时,
时,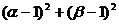 的最小值是18。
的最小值是18。
这时就可以作出正确选择,只有(B)正确。
4.对正整数n,设抛物线y2=2(2n+1)x,过点P(2n,0)作直线交抛物线于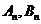 两点,则数列
两点,则数列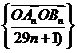 的前n和=
。
的前n和=
。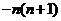
3.过圆∴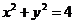 外一点M(4,-1)引圆的两条切线,则经过两切点的直线方程为
外一点M(4,-1)引圆的两条切线,则经过两切点的直线方程为
析: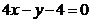 ,错误的思路是先找切点而后再直线方程,造成了很大的计算量。
,错误的思路是先找切点而后再直线方程,造成了很大的计算量。
2.2 策略性错误
策略性错误是指解题思路阻塞或一种策略产生错误导向,或指一种策略明显增加了过程的难度和复杂性,由于时间的限制,问题最终得不到解决。主要有:①方法不当,②不能正确转化问题或运用模式。(消除策略性错误的应对策略是:后期复习注意归类总结,对基础题中档题形成模式化解法)
2.若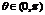 方程
方程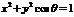 表示的曲线可以是
直线、圆、椭圆、双曲线
表示的曲线可以是
直线、圆、椭圆、双曲线
1.曲线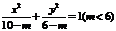 与曲线
与曲线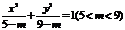 的
的
(A)焦距相等 (B) 离心率相等 (C)焦点相同 (D)准线相同
2.1基本概念数学特征不明
1.4 形式多样性:数学解题错误形式多样性是由数学知识的广泛性和个体思维的不确定性决定的。一般来说考生有解题错误有知识性错误、逻辑性错误、心理性错误、策略性的错误。
1.3 错误可避性:解题错误是在数学解题过程中形成的,是数学认识过程中的正常现象。因此高考数学解题中的错误也是可以避免的。所谓“吃一堑长一智”,就是说我们要增强数学解题过程中的错误警戒意识,养成严谨的数学思维习惯,并构建数学解题过程中常见性错误的“错题库”
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com