
25.对 ,函数
,函数 不存在极值的充要条件是
不存在极值的充要条件是
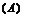 0≤
0≤ ≤21
≤21 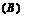
 或
或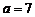

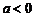 或
或

 或
或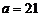
[错误形式10]转移法使用不熟练
24.设函数 ,求函数的值域。
,求函数的值域。
23.不共线的向量 ,
, 则
则 的取值范围是
的取值范围是
22.将正偶数按右表排列,则2006在第 行,第 列。

[错误形式9]限域求值,等号取舍不当
21.如图,在三角形ABC中,AB⊥AC,AD⊥BC,D是垂足,则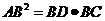 (射影定理)类似有命题:三棱锥A-BCD中AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,则有
(射影定理)类似有命题:三棱锥A-BCD中AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,则有
[错误形式8]归纳推理中,推理方向的盲目性
20.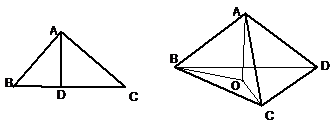 一个简单空间几何体的三视图其主视图与左视图为边长为2的正三角形,俯视图是正方形则其体积=
一个简单空间几何体的三视图其主视图与左视图为边长为2的正三角形,俯视图是正方形则其体积=

析:误将斜高当侧棱
[错误形式7]类比推理中,推理方向的盲目性
19.实数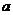 为何值时,圆
为何值时,圆 与抛物线
与抛物线 有两个公共点。
有两个公共点。
错误解法 将圆 与抛物线
与抛物线  联立,消去
联立,消去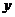 ,
,
得  ①
①
因为有两个公共点,所以方程①有两个相等正根,得 , 解之得
, 解之得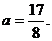

 错误分析 (如图2-2-1;2-2-2)显然,当
错误分析 (如图2-2-1;2-2-2)显然,当 时,圆与抛物线有两个公共点。
时,圆与抛物线有两个公共点。
要使圆与抛物线有两个交点的充要条件是方程①有一正根、一负根;或有两个相等正根。
当方程①有一正根、一负根时,得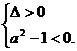 解之,得
解之,得
因此,当 或
或 时,圆
时,圆 与抛物线
与抛物线 有两个公共点。
有两个公共点。
思考题:实数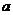 为何值时,圆
为何值时,圆 与抛物线
与抛物线 ,
,
(1) 有一个公共点;(2)有三个公共点;(3)有四个公共点;(4)没有公共点。
[错误形式6]空间图形读图平面化
18.已知数列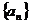 的前
的前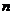 项和
项和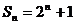 ,求
,求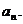
错误解法 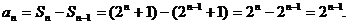
错误分析 显然,当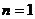 时,
时, 。
。
错误原因:没有注意公式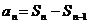 成立的条件是。
成立的条件是。
因此在运用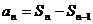 时,必须检验
时,必须检验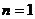 时的情形。即:
时的情形。即: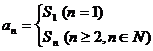 。
。
17.设等比数列 的全
的全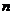 项和为
项和为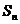 .若
.若 ,求数列的公比
,求数列的公比 .
.
错误解法 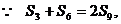
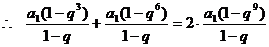 ,
,
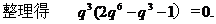
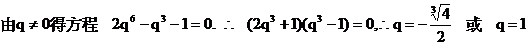 。
。
错误分析 在错解中,由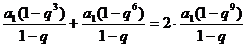 ,
,
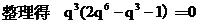 时,应有
时,应有 。
。
在等比数列中, 是显然的,但公比q完全可能为1,因此,在解题时应先讨论公比
是显然的,但公比q完全可能为1,因此,在解题时应先讨论公比 的情况,再在
的情况,再在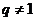 的情况下,对式子进行整理变形。
的情况下,对式子进行整理变形。
正确解法
若 ,则有
,则有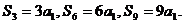 但
但 ,即得
,即得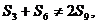 与题设矛盾,故
与题设矛盾,故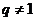 .
.
又依题意  Þ
Þ 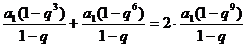 Þ
Þ  ,即
,即 因为
因为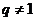 ,所以
,所以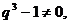 所以
所以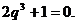 解得
解得 
说明 此题为1996年全国高考文史类数学试题第(21)题,不少考生的解法同错误解法,根据评分标准而痛失2分。
[错误形式5]忽视分类讨论,或分类不全
16.已知函数 的定义域为R,则实数
的定义域为R,则实数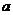 取值范围是( )
取值范围是( )
A. B.
B. C.
C. D.
D.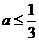
析:应选C,错误原因是只把分母看成二次函数研究,而忽视了 情况。
情况。
[错误形式4]以偏概全,错将特殊当一般
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com