
6.(湖南卷)设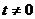 ,点P(
,点P(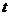 ,0)是函数
,0)是函数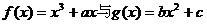 的图象的一个公共点,两函数的图象在点P处有相同的切线.;(Ⅰ)用
的图象的一个公共点,两函数的图象在点P处有相同的切线.;(Ⅰ)用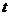 表示a,b,c;
表示a,b,c;
(Ⅱ)若函数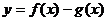 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求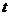 的取值范围.
的取值范围.
解:(I)因为函数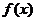 ,
, 的图象都过点(
的图象都过点(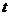 ,0),所以
,0),所以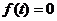 ,
,
即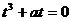 .因为
.因为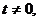 所以
所以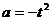 .
. 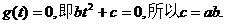
又因为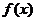 ,
, 在点(
在点(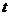 ,0)处有相同的切线,所以
,0)处有相同的切线,所以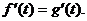
而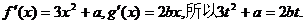
将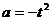 代入上式得
代入上式得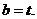 因此
因此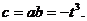 故
故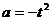 ,
,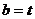 ,
,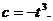
(II)解法一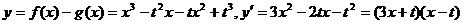 .
.
当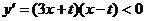 时,函数
时,函数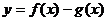 单调递减.
单调递减.
由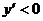 ,若
,若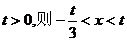 ;若
;若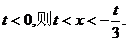
由题意,函数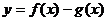 在(-1,3)上单调递减,则
在(-1,3)上单调递减,则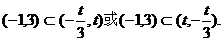
所以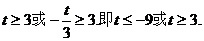
又当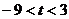 时,函数
时,函数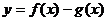 在(-1,3)上单调递减.
在(-1,3)上单调递减.
所以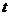 的取值范围为
的取值范围为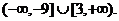
解法二: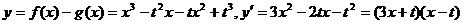
因为函数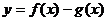 在(-1,3)上单调递减,且
在(-1,3)上单调递减,且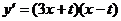 是(-1,3)
是(-1,3)
上的抛物线,
所以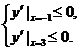 即
即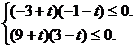 解得
解得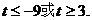
所以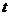 的取值范围为
的取值范围为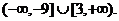
4.(全国卷Ⅱ)设a为实数,函数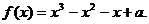 (Ⅰ)求
(Ⅰ)求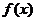 的极值.
的极值.
(Ⅱ)当a在什么范围内取值时,曲线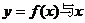 轴仅有一个交点.
轴仅有一个交点.
解:(I)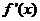 =3
=3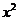 -2
-2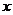 -1 若
-1 若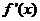 =0,则
=0,则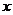 ==-
==-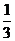 ,
,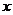 =1
=1
当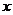 变化时,
变化时,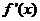 ,
,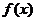 变化情况如下表:
变化情况如下表:
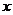 |
(-∞,-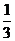 ) ) |
-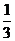 |
(-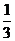 ,1) ,1) |
1 |
(1,+∞) |
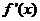 |
+ |
0 |
- |
0 |
+ |
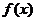 |
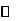 |
极大值 |
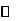 |
极小值 |
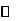 |
∴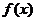 的极大值是
的极大值是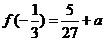 ,极小值是
,极小值是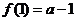
(II)函数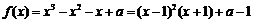 ,由此可知,取足够大的正数时,有
,由此可知,取足够大的正数时,有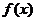 >0,取足够小的负数时有
>0,取足够小的负数时有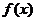 <0,所以曲线
<0,所以曲线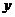 =
=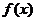 与
与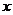 轴至少有一个交点结合
轴至少有一个交点结合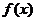 的单调性可知:
的单调性可知:
当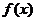 的极大值
的极大值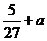 <0,即
<0,即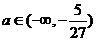 时,它的极小值也小于0,因此曲线
时,它的极小值也小于0,因此曲线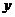 =
=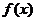 与
与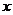 轴仅有一个交点,它在(1,+∞)上。
轴仅有一个交点,它在(1,+∞)上。
当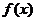 的极小值
的极小值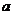 -1>0即
-1>0即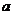
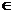 (1,+∞)时,它的极大值也大于0,因此曲线
(1,+∞)时,它的极大值也大于0,因此曲线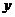 =
=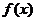 与
与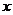 轴仅有一个交点,它在(-∞,-
轴仅有一个交点,它在(-∞,-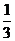 )上。∴当
)上。∴当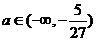 ∪(1,+∞)时,曲线
∪(1,+∞)时,曲线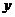 =
=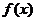 与
与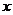 轴仅有一个交点。
轴仅有一个交点。
3.已知向量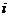 =(1,0),
=(1,0),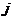 =(0,1),函数
=(0,1),函数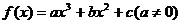 的图象在
的图象在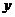 轴上的截距为1,在
轴上的截距为1,在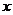 =2处切线的方向向量为
=2处切线的方向向量为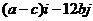 ,并且函数当
,并且函数当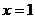 时取得极值。
时取得极值。
(1)求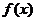 的解析式;(2)求
的解析式;(2)求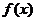 的单调递增区间;(3)求
的单调递增区间;(3)求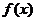 的极值。
的极值。
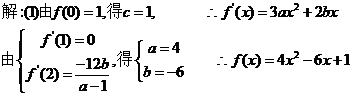
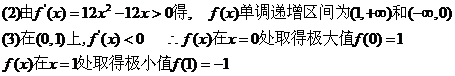
如果直线l是过P和Q的公切线,则①式和②式都是l的方程,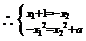
消去x2得方程 2x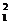 +2x2+1+a=0.
+2x2+1+a=0.
若判别式△=4-4×2(1+a)=0时,即a=-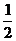 时解得x1=-
时解得x1=-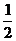 ,此时点P与Q重合.
,此时点P与Q重合.
即当a=-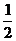 时C1和C2有且仅有一条公切线,由①得公切线方程为 y=x-
时C1和C2有且仅有一条公切线,由①得公切线方程为 y=x-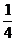 .
.
(Ⅱ)证明:由(Ⅰ)可知.当a<-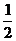 时C1和C2有两条公切线
时C1和C2有两条公切线
设一条公切线上切点为:P(x1,y1), Q(x2 , y2 ).
其中P在C1上,Q在C2上,则有x1+x2=-1,
y1+y2=x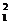 +2x1+(-x
+2x1+(-x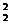 +a)= x
+a)= x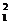 +2x1-(x1+1)2+a=-1+a .
+2x1-(x1+1)2+a=-1+a .
线段PQ的中点为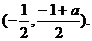 同理,另一条公切线段P′Q′的中点也是
同理,另一条公切线段P′Q′的中点也是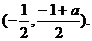
所以公切线段PQ和P′Q′互相平分.
2.已知f(x)=x2+ax+b, g(x)=x2+cx+d,又f(2x+1)=4g(x),且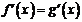 ,f(5)=30,则求g(4)。
,f(5)=30,则求g(4)。
解: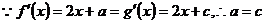 ∵f(2x+1)=4g(x)
∴
∵f(2x+1)=4g(x)
∴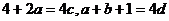
∴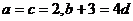 又 f(5)=30=25+10+b ∴b=-5 d=
又 f(5)=30=25+10+b ∴b=-5 d=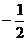 ∴g(x)=x2+2x
∴g(x)=x2+2x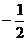 ∴g(4)=
∴g(4)=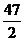
函数y=-x2+a的导数y′=-2x, 曲线C2 在点Q(x2,-x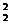 +a)的切线方程是
+a)的切线方程是
1.已知抛物线C1:y=x2+2x和C:y=-x2+a,如果直线l同时是C1和C2的切线,称l是C1和C2的公切线,公切线上两个切点之间的线段,称为公切线段.
(Ⅰ)a取什么值时,C1和C2有且仅有一条公切线?写出此公切线的方程;
(Ⅱ)若C1和C2有两条公切线,证明相应的两条公切线段互相平分.
解:本小题主要考查导数、切线等知识及综合运用数学知识解决问题的能力,满分12分
(Ⅰ)解:函数y=x2+2x的导数y′=2x+2,曲线C1在点P(x1,x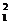 +2x1)的切线方程是:
+2x1)的切线方程是:
10.解析:曲线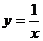 和
和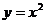 在它们的交点坐标是(1,1),两条切线方程分别是y=-x+2和y=2x-1,它们与
在它们的交点坐标是(1,1),两条切线方程分别是y=-x+2和y=2x-1,它们与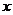 轴所围成的三角形的面积是
轴所围成的三角形的面积是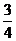 .
.
9.设函数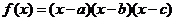 ,(
,(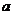 、
、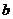 、
、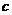 是两两不等的常数),则
是两两不等的常数),则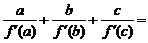 .0
.0
8.过点(-1,0)作抛物线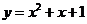 的切线,则其中一条切线为 ( )
的切线,则其中一条切线为 ( )
(A)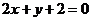 (B)
(B)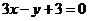 (C)
(C)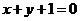 (D)
(D)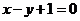
小题答案:
7.函数f(x)=x(x-1)(x-2)·…·(x-100)在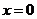 处的导数值为 ( )
处的导数值为 ( )
A.0 B.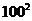 C.200
.100!
C.200
.100!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com