
7.(全国卷Ⅰ)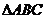 的外接圆的圆心为O,两条边上的高的交点为H,
的外接圆的圆心为O,两条边上的高的交点为H,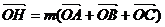 ,则实数m = 1
,则实数m = 1
[典型考例]
[问题1]三角形内角和定理的灵活运用
例1.(2005湖南卷)已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C的大小.
解法一 由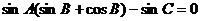
得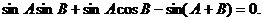
所以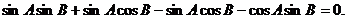
即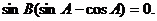
因为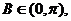 所以
所以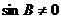 ,从而
,从而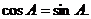
由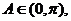 知
知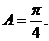 从而
从而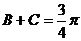 .
.
由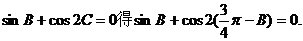
即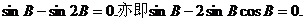
由此得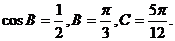 所以
所以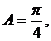
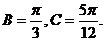
解法二:由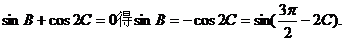
由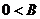 、
、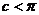 ,所以
,所以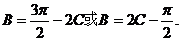 即
即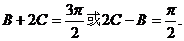
由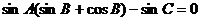 得
得 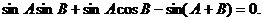
所以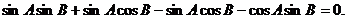
即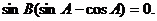 因为
因为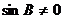 ,所以
,所以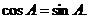
由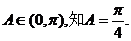 从而
从而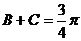 ,知B+2C=
,知B+2C=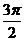 不合要求.
不合要求.
再由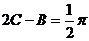 ,得
,得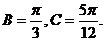 所以
所以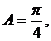
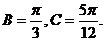
例2.[2004年全国高考(四川云南吉林黑龙江)理科数学第17题,文科数学第18题].
已知锐角三角形ABC中,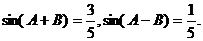
(Ⅰ)求证: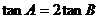 ; (Ⅱ)设AB=3,求AB边上的高.
; (Ⅱ)设AB=3,求AB边上的高.
解:(Ⅰ)证明: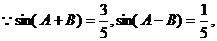
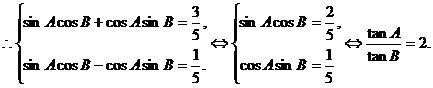
所以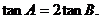
(Ⅱ)解: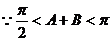 ,
,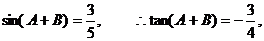
即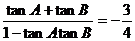 ,将
,将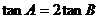 代入上式并整理得
代入上式并整理得
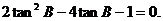
解得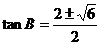 ,舍去负值得
,舍去负值得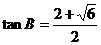 ,
,
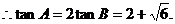 设AB边上的高为CD.则AB=AD+DB=
设AB边上的高为CD.则AB=AD+DB=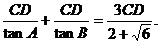
由AB=3,得CD=2+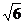 . 所以AB边上的高等于2+
. 所以AB边上的高等于2+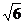 .
.
[问题2]正弦定理、余弦定理、面积公式的灵活应用
例3:在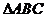 中,
中,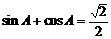 ,
,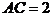 ,
,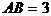 ,求
,求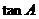 的值和
的值和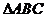 的面积.
的面积.
解法一: 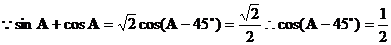 ,又
,又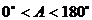
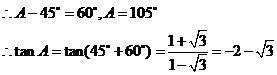
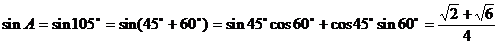
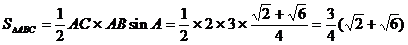
例4..(2005年湖北文分)
在△ABC中,已知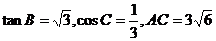 ,求△ABC的面积.
,求△ABC的面积.
解.本小题主要考查正弦定理、余弦定理和三角形面积公式等基础知识,同时考查利用三角公式进行恒等变形的技能和运算能力.
解法1:设AB、BC、CA的长分别为c、a、b,
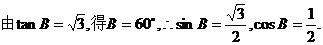
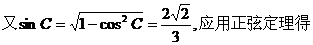
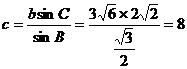 .
.
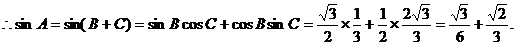
故所求面积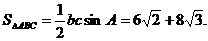
解法3:同解法1可得c=8. 又由余弦定理可得
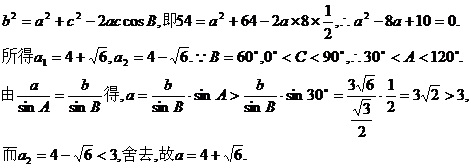
故所求面积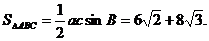
例5.(2005年湖北理) 在△ABC中,已知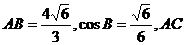 边上的中线BD=
边上的中线BD=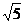 ,求sinA的值.
,求sinA的值.
解.本小题主要考查正弦定理、余弦定理等基础知识,同时考查利用三角公式进行恒等变形的技能和运算能力.
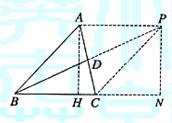
解法1:设E为BC的中点,连接DE,则DE//AB,且DE=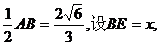
在△BDE中利用余弦定理可得: BD2=BE2+ED2-2BE·EDcosBED,
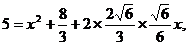
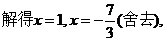
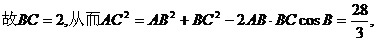
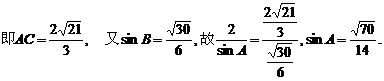
解法2:
以B为坐标原点,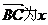 轴正向建立直角坐标系,且不妨设点A位于第一象限.
轴正向建立直角坐标系,且不妨设点A位于第一象限.
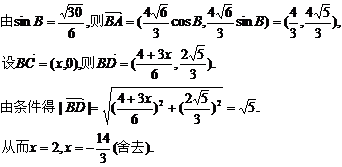
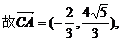
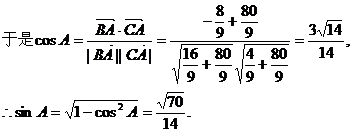
解法3:过A作AH⊥BC交BC于H,延长BD到P使BD=DP,连接AP、PC,
过P作PN⊥BC交BC的延长线于N,则HB=ABcosB=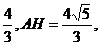
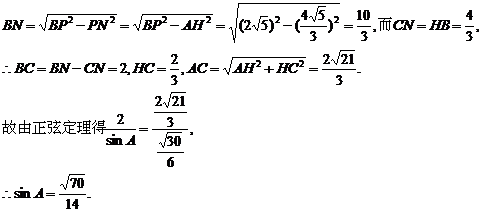
[问题3]向量与解三角形
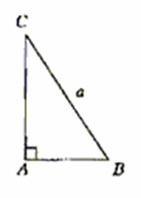
例6.(2004年湖北高考数学·理工第19题,文史第19题,本小题满分12分)
如图,在Rt△ABC中,已知BC=a,若长为2a的线段PQ以点A为中点,问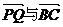
的夹角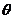 取何值时
取何值时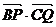 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.
6.(福建卷)在△ABC中,∠C=90°,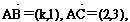 则k的值是 ( D )
则k的值是 ( D )
A.5 B.-5 C.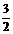 D.
D.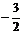
5.(湖北卷)若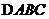 的内角
的内角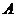 满足
满足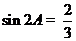 ,则
,则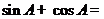
A.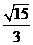 B.
B.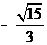 C.
C.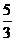 D.
D.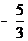
解:由sin2A=2sinAcosA>0,可知A这锐角,所以sinA+cosA>0,又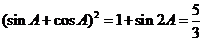 ,故选A
,故选A
4.△ABC中,a、b、c分别为∠A、∠B、∠C的对边.如果a、b、c成等差数列,
∠B=30°,△ABC的面积为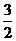 ,那么b= ( )
,那么b= ( )
A.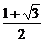 B.
B.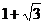 C.
C.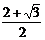 D.
D.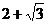
3.(江西卷)在△OAB中,O为坐标原点,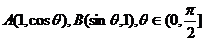 ,则当△OAB的面积达最大值时,
,则当△OAB的面积达最大值时,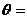 ( D )
A.
( D )
A.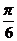 B.
B.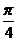 C.
C.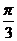 D.
D.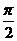
2.(全国卷Ⅱ)锐角三角形的内角A 、B 满足tan A - 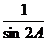 = tan B,则有
= tan B,则有
(A)sin 2A –cos B = 0 (B)sin 2A + cos B = 0 (C)sin 2A – sin B = 0 (D) sin 2A+ sin B = 0
1.(全国卷Ⅰ)在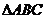 中,已知
中,已知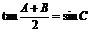 ,给出以下四个论断: B
,给出以下四个论断: B
① 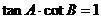 ②
② 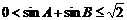 ③
③ 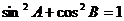 ④
④ 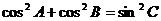
其中正确的是(A)①③ (B)②④ (C)①④ (D)②③
18.略解(Ⅰ)设点P(x , y),分别计算出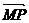 ·
·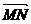 ,
,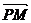 ·
·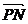 ,
,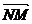 ·
·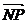 ,
,
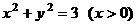 由题意,可得点P的轨迹方程是
由题意,可得点P的轨迹方程是
故点P 的轨迹是以原点为圆心、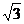 为半径的右半圆.
为半径的右半圆.
(Ⅱ) 由(Ⅰ)知,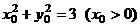 ,可得cosθ=
,可得cosθ=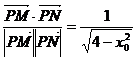 ,
,
又x0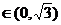 ,∴
,∴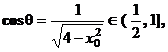 即
即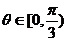 ,
,
于是sinθ=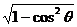 =
=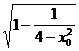 =
=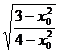 =
=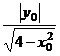 ,
,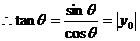
17. 略解 (1)y2=4x (x>0) (2)先证明l与x轴不垂直,再设l的方程为
y=kx+b(k≠0),A(x1,y1),B(x2,y2).联立直线与抛物线方程,得
ky2- 4y+4b=0,由 ,得
,得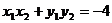 .
.
又 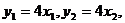 故
故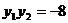 而
而 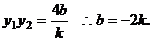
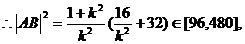
解得直线l的斜率的取值范围是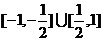
16.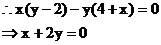 解:因为G是边长为1的正三角形ABC的中心,
解:因为G是边长为1的正三角形ABC的中心,
所以 AG=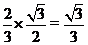 ,ÐMAG=
,ÐMAG=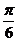 ,
,
由正弦定理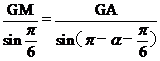 ,得
,得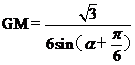
则S1=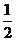 GM·GA·sina=
GM·GA·sina=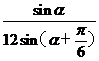 同理可求得S2=
同理可求得S2=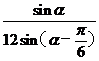
(1) y=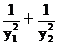 =
=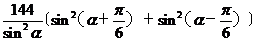
=72(3+cot2a)因为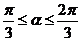 ,所以当a=
,所以当a=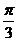 或a=
或a=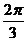 时,y取得最大值ymax=240
时,y取得最大值ymax=240
当a=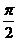 时,y取得最小值ymin=216
时,y取得最小值ymin=216
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com