
2.解综合题要总揽全局,尤其要注意上一问的结论可作为下面论证的已知条件,在后面求解的过程中适时应用.
[问题3]函数与数列的综合题 P51 例3
数列是一特殊的函数,其定义域为正整数集,且是自变量从小到大变化时函数值的序列。注意深刻理解函数性质对数列的影响,分析题目特征,探寻解题切入点.
P51 例3(2006湖北卷)已知二次函数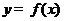 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为 ,数列
,数列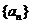 的前n项和为
的前n项和为 ,点
,点 均在函数
均在函数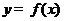 的图像上。(Ⅰ)、求数列
的图像上。(Ⅰ)、求数列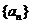 的通项公式;(Ⅱ)、设
的通项公式;(Ⅱ)、设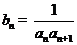 ,
,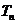 是数列
是数列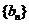 的前n项和,求使得
的前n项和,求使得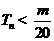 对所有
对所有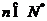 都成立的最小正整数m;
都成立的最小正整数m;
点评:本题考查二次函数、等差数列、数列求和、不等式等基础知识和基本的运算技能,考查分析问题的能力和推理能力。
解:(Ⅰ)设这二次函数f(x)=ax2+bx (a≠0) ,则 f`(x)=2ax+b,由于f`(x)=6x-2,得
a=3 , b=-2, 所以 f(x)=3x2-2x.
又因为点 均在函数
均在函数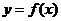 的图像上,所以
的图像上,所以 =3n2-2n.
=3n2-2n.
当n≥2时,an=Sn-Sn-1=(3n2-2n)-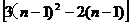 =6n-5.
=6n-5.
当n=1时,a1=S1=3×12-2=6×1-5,所以,an=6n-5 (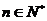 )
)
(Ⅱ)由(Ⅰ)得知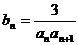 =
=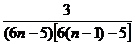 =
= ,
,
故Tn=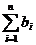 =
=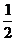
 =
=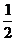 (1-
(1-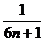 ).
).
因此,要使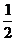 (1-
(1-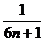 )<
)<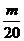 (
(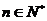 )成立的m,必须且仅须满足
)成立的m,必须且仅须满足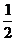 ≤
≤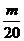 ,即m≥10,所以满足要求的最小正整数m为10.
,即m≥10,所以满足要求的最小正整数m为10.
4.[例],已知数列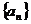 中,
中,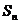 是其前
是其前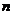 项和,并且
项和,并且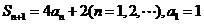 ,⑴设数列
,⑴设数列 ,求证:数列
,求证:数列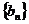 是等比数列;⑵设数列
是等比数列;⑵设数列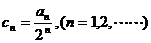 ,求证:数列
,求证:数列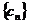 是等差数列;⑶求数列
是等差数列;⑶求数列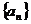 的通项公式及前
的通项公式及前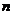 项和。
项和。
分析:由于{b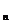 }和{c
}和{c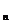 }中的项都和{a
}中的项都和{a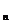 }中的项有关,{a
}中的项有关,{a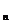 }中又有S
}中又有S =4a
=4a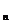 +2,可由S
+2,可由S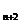 -S
-S 作切入点探索解题的途径.
作切入点探索解题的途径.
[注2]本题立意与2007年高考题文科20题结构相似.
解:(1)由S =4a
=4a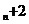 ,S
,S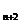 =4a
=4a +2,两式相减,得S
+2,两式相减,得S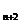 -S
-S =4(a
=4(a -a
-a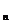 ),即a
),即a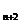 =4a
=4a -4a
-4a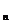 .(根据b
.(根据b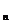 的构造,如何把该式表示成b
的构造,如何把该式表示成b 与b
与b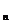 的关系是证明的关键,注意加强恒等变形能力的训练)
的关系是证明的关键,注意加强恒等变形能力的训练)
a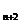 -2a
-2a =2(a
=2(a -2a
-2a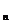 ),又b
),又b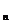 =a
=a -2a
-2a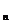 ,所以b
,所以b =2b
=2b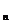 ①
①
已知S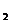 =4a
=4a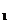 +2,a
+2,a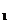 =1,a
=1,a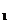 +a
+a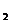 =4a
=4a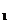 +2,解得a
+2,解得a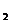 =5,b
=5,b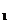 =a
=a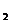 -2a
-2a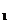 =3 ②
=3 ②
由①和②得,数列{b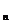 }是首项为3,公比为2的等比数列,故b
}是首项为3,公比为2的等比数列,故b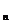 =3·2
=3·2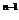 .
.
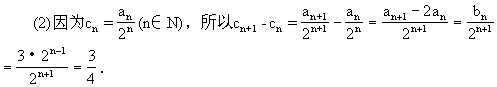


当n≥2时,S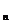 =4a
=4a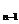 +2=2
+2=2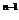 (3n-4)+2;当n=1时,S
(3n-4)+2;当n=1时,S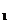 =a
=a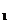 =1也适合上式.
=1也适合上式.
综上可知,所求的求和公式为S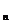 =2
=2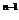 (3n-4)+2.
(3n-4)+2.
说明:1.本例主要复习用等差、等比数列的定义证明一个数列为等差,等比数列,求数列通项与前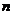 项和。解决本题的关键在于由条件
项和。解决本题的关键在于由条件 得出递推公式。
得出递推公式。
3. (全国卷Ⅰ) 设正项等比数列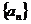 的首项
的首项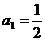 ,前n项和为
,前n项和为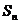 ,且
,且 。(Ⅰ)求
。(Ⅰ)求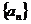 的通项;(Ⅱ)求
的通项;(Ⅱ)求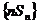 的前n项和
的前n项和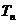 。
。
解:(Ⅰ)由 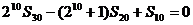 得
得 
即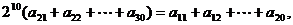
可得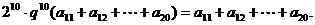
因为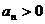 ,所以
,所以 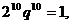 解得
解得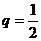 ,因而
,因而 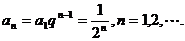
(Ⅱ)因为 是首项
是首项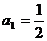 、公比
、公比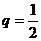 的等比数列,故
的等比数列,故
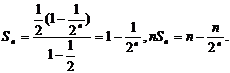
则数列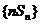 的前n项和
的前n项和 
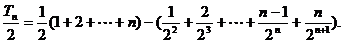
前两式相减,得 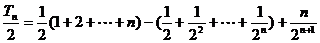
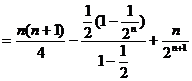 即
即
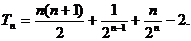
[问题2]等差、等比数列的判定问题.P53 T7 例P54 T9
[例]P54 T9(上海卷)已知有穷数列
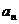
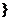 共有2
共有2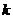 项(整数
项(整数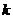 ≥2),首项
≥2),首项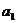 =2.设该数列的前
=2.设该数列的前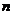 项和为
项和为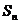 ,且
,且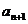 =
=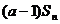 +2(
+2(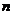 =1,2,┅,2
=1,2,┅,2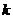 -1),其中常数
-1),其中常数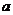 >1.
>1.
(1)求证:数列
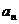
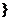 是等比数列;(2)若
是等比数列;(2)若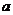 =2
=2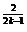 ,数列
,数列
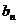
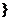 满足
满足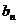 =
=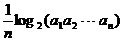 (
(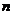 =1,2,┅,2
=1,2,┅,2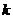 ),求数列
),求数列
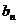
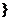 的通项公式;
的通项公式;
(3)若(2)中的数列
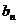
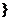 满足不等式|
满足不等式|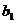 -
-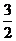 |+|
|+|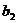 -
-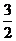 |+┅+|
|+┅+|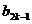 -
-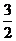 |+|
|+|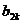 -
-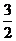 |≤4,求
|≤4,求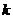 的值.
的值.
(1) [证明] 当n=1时,a2=2a,则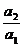 =a;
=a;
2≤n≤2k-1时, an+1=(a-1) Sn+2, an=(a-1) Sn-1+2,
an+1-an=(a-1) an, ∴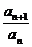 =a, ∴数列{an}是等比数列.
=a, ∴数列{an}是等比数列.
(2) 解:由(1) 得an=2a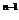 , ∴a1a2…an=2
, ∴a1a2…an=2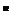 a
a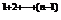 =2
=2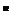 a
a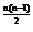 =2
=2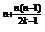 ,
,
bn=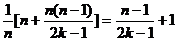 (n=1,2,…,2k).
(n=1,2,…,2k).
(3)设bn≤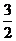 ,解得n≤k+
,解得n≤k+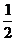 ,又n是正整数,于是当n≤k时, bn<
,又n是正整数,于是当n≤k时, bn<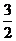 ;
;
当n≥k+1时, bn>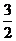 .
.
原式=(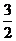 -b1)+(
-b1)+(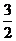 -b2)+…+(
-b2)+…+(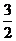 -bk)+(bk+1-
-bk)+(bk+1-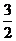 )+…+(b2k-
)+…+(b2k-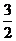 )
)
=(bk+1+…+b2k)-(b1+…+bk)
=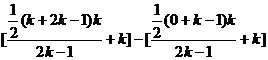 =
=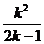 .
.
当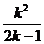 ≤4,得k2-8k+4≤0,
4-2
≤4,得k2-8k+4≤0,
4-2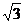 ≤k≤4+2
≤k≤4+2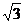 ,又k≥2,
,又k≥2,
∴当k=2,3,4,5,6,7时,原不等式成立.
2.(上海卷)设数列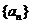 的前
的前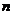 项和为
项和为 ,且对任意正整数
,且对任意正整数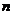 ,
,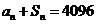 。(1)求数列
。(1)求数列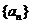 的通项公式?(2)设数列
的通项公式?(2)设数列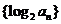 的前
的前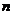 项和为
项和为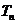 ,对数列
,对数列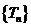 ,从第几项起
,从第几项起 ?
?
.解(1) ∵an+ Sn=4096, ∴a1+ S1=4096, a1 =2048.
当n≥2时, an= Sn-Sn-1=(4096-an)-(4096-an-1)= an-1-an ∴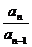 =
=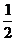 an=2048(
an=2048(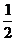 )n-1.
)n-1.
(2) ∵log2an=log2[2048(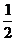 )n-1]=12-n, ∴Tn=
)n-1]=12-n, ∴Tn=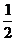 (-n2+23n).
(-n2+23n).
由Tn<-509,解得n>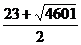 ,而n是正整数,于是,n≥46. ∴从第46项起Tn<-509.
,而n是正整数,于是,n≥46. ∴从第46项起Tn<-509.
[问题1]等差、等比数列的项与和特征问题P49 例1 3。P50 例2 P56 例1 P59 T6.
[注1]文中所列例题如末给题目原文均为广州市二轮复习资料上例题
例(四川卷)数列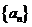 的前
的前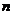 项和记为
项和记为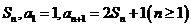 (Ⅰ)求
(Ⅰ)求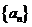 的通项公式;(Ⅱ)等差数列
的通项公式;(Ⅱ)等差数列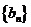 的各项为正,其前
的各项为正,其前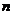 项和为
项和为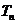 ,且
,且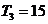 ,又
,又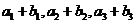 成等比数列,求
成等比数列,求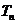
本小题主要考察等差数列、等比数列的基础知识,以及推理能力与运算能力。满分12分。
解:(Ⅰ)由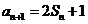 可得
可得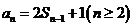 ,两式相减得
,两式相减得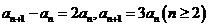
又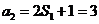 ∴
∴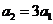 故
故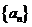 是首项为
是首项为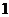 ,公比为
,公比为 得等比数列 ∴
得等比数列 ∴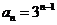
(Ⅱ)设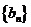 的公比为
的公比为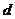 由
由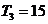 得,可得
得,可得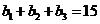 ,可得
,可得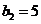
故可设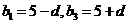 又
又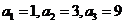
由题意可得 解得
解得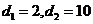
∵等差数列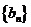 的各项为正,∴
的各项为正,∴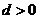 ∴
∴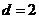 ∴
∴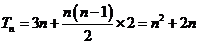
1.设等差数列{an}的首项a1及公差d都为整数,前n项和为Sn.
(Ⅰ)若a11=0,S14=98,求数列{an}的通项公式;
(Ⅱ)若a1≥6,a11>0,S14≤77,求所有可能的数列{an}的通项公式
5.解综合题的成败在于审清题目,弄懂来龙去脉,透过给定信息的表象,抓住问题的本质,揭示问题的内在联系和隐含条件,明确解题方向,形成解题策略.
4.数列极限的综合题形式多样,解题思路灵活,但万变不离其宗,就是离不开数列极限的概念和性质,离不开数学思想方法,只要能把握这两方面,就会迅速打通解题思路.
3.注意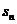 与
与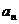 之间关系的转化。如:
之间关系的转化。如: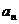 =
=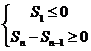
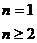 ,
, 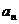 =
=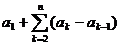 .
.
2.在解决等差数列或等比数列的相关问题时,“基本量法”是常用的方法,但有时灵活地运用性质,可使运算简便,而一般数列的问题常转化为等差、等比数列求解。
1.证明数列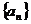 是等差或等比数列常用定义,即通过证明
是等差或等比数列常用定义,即通过证明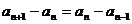 或
或 而得。
而得。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com