3.下列各句中，没有语病、句意明确的一句是(　 )

A．中新网2月4日电据美国媒体报道，基地老二网上再次现声，指责奥巴马未在就职演说中提及加沙，呼吁穆斯林报复美国支持以色列进攻加沙。

B．中国政府历来主张通过法律和外交手段，按照国际社会处理非法流失文物返还问题，依靠国际合作追索非法流失海外的中国文物。

C．总体说来，山寨文化的泛滥与其说是对草根创新精神的彰显和标榜，不如说是对国人知识产权意识严重缺乏的揭露与讽刺。

D北京奥运会期间，具有悠久历史的长城、十三陵、故宫、颐和园等无不以其迷人的风姿和厚重的文化积淀为中外游客所倾倒。

2.下列各句中，加点的成语使用恰当的一项是(　 )

A．北京时间8月24日8时，第29届奥运会在北京落下帷幕，虽然奥林匹克圣火缓缓熄灭，但精彩的奥运会闭幕式表演让北京奥运会更显得曲尽其妙。

B．对身居官位者写出的散文，一些报刊便门户大开，一些评论家便极力捧场，这种把散文和权势捆绑在一起的做法无异于焚琴煮鹤。

C．从2008年秋季学期开始，国家免除了城市义务教育阶段学生的学杂费，至此，城乡免费九年义务教育全面实现，我国“义务教育”终于实至名归。

D.《梅兰芳》作为陈凯歌的回归之作，虽然比起《霸王别姬》还稍有差距，但相较于前几年口碑极差的《无极》，媒体和大众给些过分的溢美之词还是可以理解的。

1.下列各组词语中，没有错别字的一组是(　 )

A．遒劲　　　 敲竹杠　　　 沸反盈天　　　 来而不往非理也

B．丰腴　　　 打圆场　 　 煊赫一时　　　 识时务者为俊杰

C．撕打　　　 跑龙套　　 　有条不紊　　　 言必信，行必果

D．接洽　　　 挂幌子　 　 德艺双罄　　　 牵一发而动全身

6. [巩固]B，

4. [巩固] C, [迁移]B，5. [举例]-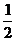，[巩固]

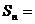
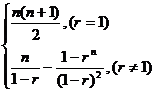
1. [巩固]C，[迁移]视S_n为关于n的二次函数，其图象是经过原点的抛物线上的点，故选B，2. [巩固]==≥=，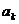

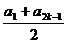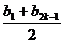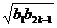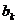[迁移]等比数列中奇数项的符号相同，偶数项的符号也相同；- ，，± ，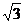

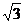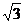[提高] S_n-S_n-5=a_n+a_n-1+a_n-2+a_n-3+a_n-4=55,与a₁+a₂+a₃+a₄+a₅=25两式相加得5(a₁+a_n)=80,得n=8，3.[巩固]6；

6.解等差(比)数列有关通项、求和问题时别忘了“基本元”，即把问题转化为首项a₁，公差d(或公比q)的方程(组)或不等式(组)去处理。已知等差或等比数列中的任两项也可用 a_m-a_n=(m-n)d，或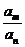=q^m-n。

[举例1] 等差数列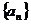的前n项和S_n，若S₃=9，S₁₃=26求S₂₃的值。

解析：用求和公式解方程组，求出a₁,d,再代入求和公式中求S₂₃，这是通法。也可简化为：

S₃=3a₂=9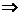a₂=3，S₁₃=13a₇=26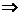a₇=2, ∴a₁₂= 1(a₂、a₇、a₁₂成等差数列)，S₂₃=23a₁₂=23。

[举例2]已知等差数列{a_n}中，a₃与a₅的等差中项等于2，又a₄与a₆的等比中项等于6，则a₁₀等于　 (A) 54　　 (B) 50　　 (C) 26　　 (D) 16

解析：a₃与a₅的等差中项等于2，即a₄=2；a₄与a₆的等比中项等于6，即a₆=18；于是2d=16,

a₁₀= a₆+4d=50,选B。

[巩固]]已知等差数列{a_n}的首项a₁=120，公差d=－4，若S_n≤a_n(n>1)，则n的最小值为　　　　　　　　　　　　 　　　　　　　　　　　

(A)61　　 (B)62　　 (C)63　　 　(D)70

[迁移]等差数列{a_n}中若a_m=n，a_n=m且m≠n求证：a_m+n=0；

简答

5.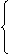注意：等比数列求和公式是一个分段函数　 　　　na₁ (q=1)

　　　　　　　　　　　　　　　　　　 　　Sn=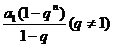 　

则涉及到等比数列求和时若公比不是具体数值须分类讨论解题。

[举例]已知等比数列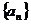的公比为q，前n项和为S_n，且S₃ ，S₉ ，S₆ 成等差数列，求q³的值。

解析：不可直接用等比数列的求和公式，需讨论：若q=1，S₃=3a₁ ，S₉=9a₁，S₆=6a₁,则有：

18a₁=3a₁+6a₁, 则a₁=0, 与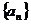是等比数列矛盾，∴q≠1，于是有：

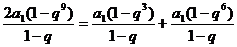，化简得：，∴。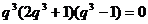

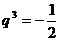本题还可以用：第一个三项和、第二个三项和、第三个三项和成等比数列解决，留读者自己完成。

[巩固]已知a_n=1+r+r²+r³+…r^n-1，则数列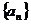的前n项和=______________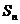

4. 等差数列当首项a₁>0且公差d<0，前n项和存在最大值。利用不等式组：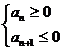

确定n值，即可求得S_n的最大值。等差数列当首项a₁<0且公差d>0时，前n项和存在最小值。 类似地确定n值，即可求得s_n的最小值；也可视s_n为关于n的二次函数，通过配方求最值；还可以利用二次函数的图象来求。

[举例] 设等差数列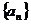满足3 a₈=5a₁₃，且a₁>0，则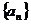的前__________项和最大

解析：思路一：由3 a₈=5a₁₃得：d=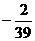a₁,若前n项和最大，则，

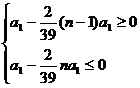又a₁>0得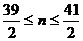：，∴n=20,即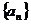的前20项和最大。这一做法最通行。

思路二：S_n=na₁+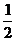n(n-1)d=na₁- 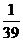n(n-1)a₁=-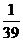a₁(n²-40n),当且仅当n=20时S_n最大。这一做法突显了数列的函数特征。思路三：由3 a₈=5a₁₃得15a₈=25a₁₃,即S₁₅=S₂₅,又∵a₁>0，

∴S_n的图象是开口向下的抛物线上的点列，对称轴恰为n=20，故n=20时S_n最大。这一做法中几乎没有运算，但设计太过“精妙”，非对等差数列的性质融会贯通而不能为，仅供欣赏。

[巩固] 数列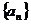是等差数列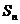，是其前n项和，且S₅＜S₆，S₆=S₇>S₈，则下列结论错误的是：A.d ＜0　 　B.a₇=0 　C.S₉>S₅ 　　D. S₆ ,S₇均为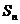的最大值　 (　　 )

[迁移] 在等差数列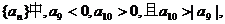则在前n项和S_n中最大的负数为

　　　 A．S₁₆ B．S₁₇ C．S₁₈ D．S₁₉(　　 )

3．等差数列前n项和、次n项和、再后n项和(即连续相等项的和)仍成等差数列；等比数列前n项和(和不为0)、次n项和、再后n项和仍成等比数列。

[举例1]在等比数列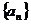中，S₂ =40，S₄ =60，则S₆等于　　　　　　　 (　　 )

　 A　 10　　 　　　　B　 70　　　　　　　　 C　 80　　　 　　　D　 90

解析：在等比数列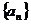中，第一个两项和为40，第二个两项和为20(注意：S₄是前4项和，不是两项和)，则第三个两项和为10，S₆为三个两项和相加，选B。

[举例2] 在等差数列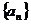中，前n项之和为,已知S₃=4，S₁₈-S₁₅=12，则S₁₈=　　　　

解析：在等差数列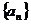中，第一个三项和为4，第六个三项和为12，S₁₈即首项为4，末项为12的等差数列的6项和，为48。

[巩固]在等差数列{a_n}中,其前n项和为S_n,已知S₅=2-b,S₁₀=4-b,则S₁₅=_________