
5、偶函数 在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,则方程
在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,则方程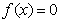 在区间[-a,a]内根的个数是 ( )
在区间[-a,a]内根的个数是 ( )
A.1 B.2 C.3 D.0
4、设等差数列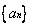 的前n项和为
的前n项和为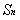 ,若则
,若则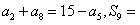 ( )
( )
A.18 B.36 C.45 D.60
3、在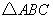 中,
中,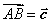 ,
,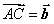 .若点
.若点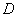 满足
满足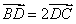 ,则
,则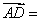 ( )
( )
A 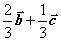 B
B 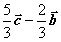 C
C 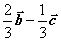 D
D 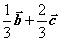
2、已知角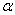 终边过点
终边过点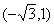
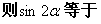 ( )
( )
A.
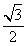 B.
B.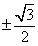 C
C 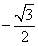 D
D 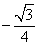
1、函数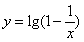 的定义域是 ( )
的定义域是 ( )
A.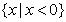 B.
B.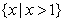 C.
C.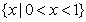 D.
D.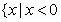 或
或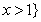
(18) 本题主要考查三角函数恒等变换及图象的对称性等基础知识, 同时考查运算求解能力。满分14分。
(Ⅰ) 解:因为f (x) =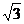 sin2x-cos2x
sin2x-cos2x
= 2sin(2x-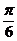 ) ,
) ,
所以f (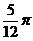 ) = 2sin
) = 2sin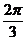 =
=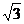 .
……………………(7分)
.
……………………(7分)
(Ⅱ) 解: 令2x-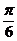 = k
= k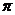 +
+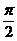 (k∈Z), 得
(k∈Z), 得
 x=
x=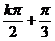 ,
,
所以函数f (x)图象的对称轴方程是x=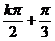 (k∈Z). ……………(14分)
(k∈Z). ……………(14分)
(19) 本题主要考查空间线线、线面、面面位置关系, 线面角大小计算, 同时考查空间想象能力和推理论证能力。满分14分。
(Ⅰ) 证明: 如图, 连结BD, 则E是BD的中点.
又F是PB的中点,
所以EF∥PD.
因为EF不在平面PCD内,
所以EF∥平面PCD. …………………(6分)
(Ⅱ) 解: 连结PE.
因为ABCD是正方形,
所以BD⊥AC.
又PA⊥平面ABC,
所以PA⊥BD.
因此BD⊥平面PAC.
故∠EPD是PD与平面PAC所成的角.
因为EF∥PD,
所以EF与平面PAC所成的角的大小等于∠EPD.
因为PA=AB=AD, ∠PAD=∠BAD=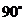 ,
,
所以Rt△PAD ≌ Rt△BAD.
因此PD=BD.
在Rt△PED中,
sin∠EPD=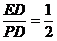 ,
,
∠EPD=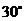 .
.
所以EF与平面PAC所成角的大小是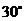 . …………………(14分)
. …………………(14分)
(20) 本题主要考查数列递推关系,等比数列的定义,求和公式等基础知识,同时考查运算求解能力。满分14分。
(Ⅰ) 解: 由 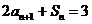 , 得
, 得
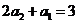 ,
,
又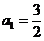 ,
,
所以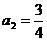 .
.
由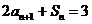 ,
, 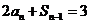 (n≥2)相减, 得
(n≥2)相减, 得
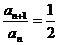 ,
,
又 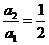 ,
,
所以数列{an}是以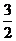 为首项,以
为首项,以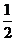 为公比的等比数列.
为公比的等比数列.
因此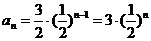 ( n∈N*).
…………………(7分)
( n∈N*).
…………………(7分)
(Ⅱ) 解: 由题意与(Ⅰ), 得
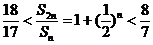 ,
,
即 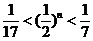 .
.
因为 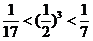 ,
, 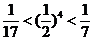 ,
,
所以n的值为3, 4. …………………(14分)
(21) 本题主要考查函数的单调性、最值等基本性质、导数的应用等基础知识, 同时考查抽象概括能力和运算求解能力。
(Ⅰ) 解: 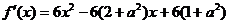
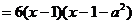 ,
,
因为函数f (x)在R上单调,
所以 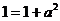 ,
,
即a = 0. …………………(6分)
(Ⅱ) 解: 因为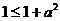 ,
,
所以 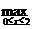 {f (x)}= max{ f (1) , f (2)}= max{3a2+3,
5}=5,
{f (x)}= max{ f (1) , f (2)}= max{3a2+3,
5}=5,
即 3a2+3 ≤ 5,
解此不等式, 得
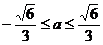 ,
,
所以a的取值范围是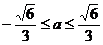 .
…………………(15分)
.
…………………(15分)
(22) 本题主要考查抛物线的几何性质,直线与抛物线的位置关系等基础知识,考查解析几何的基本思想方法和综合解题能力。满分15分。
(Ⅰ) 解: 设抛物线C的方程是x2 = ay,
则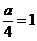 ,
,
即a = 4 .
故所求抛物线C的方程为x2 = 4y . …………………(5分)
(Ⅱ) 解:设P(x1, y1), Q(x2, y2) ,
则抛物线C在点P处的切线方程是
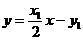 ,
,
直线PQ的方程是
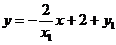 .
.
将上式代入抛物线C的方程, 得
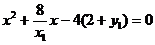 ,
,
故 x1+x2=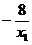 , x1x2=-8-4y1,
, x1x2=-8-4y1,
所以 x2=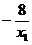 -x1 , y2=
-x1 , y2=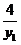 +y1+4 .
+y1+4 .
而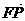 =(x1, y1-1),
=(x1, y1-1), 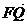 =(x2,
y2-1),
=(x2,
y2-1),
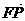 ×
×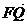 =x1 x2+(y1-1) (y2-1)
=x1 x2+(y1-1) (y2-1)
=x1 x2+y1 y2-(y1+y2)+1
=-4(2+y1)+ y1(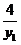 +y1+4)-(
+y1+4)-(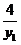 +2y1+4)+1
+2y1+4)+1
=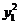 -2y1 -
-2y1 -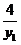 -7
-7
=(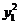 +2y1+1)-4(
+2y1+1)-4(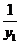 +y1+2)
+y1+2)
=(y1+1)2-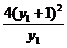
=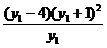
=0,
故 y1=4, 此时, 点P的坐标是(±4,4) .
经检验, 符合题意.
所以, 满足条件的点P存在, 其坐标为P(±4,4). ………………(15分)
(11) 0 (12) 过原点的平面(原点,平面每对一个得2分) (13) 1
(14) 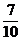 (15)
1
(16) 169 (17)
(-∞,2]
(15)
1
(16) 169 (17)
(-∞,2]
(1) B (2) A (3) D (4) A (5) C
(6) D (7) C (8) A (9) B (10) A
(18)(本题满分14分) 已知函数f (x)=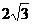 sinxcosx-2cos2x
+1.
sinxcosx-2cos2x
+1.
(Ⅰ) 求f
(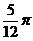 );
);
(Ⅱ) 求函数f (x)图象的对称轴方程.
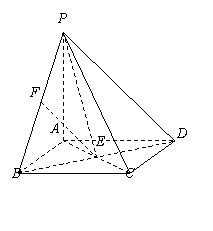
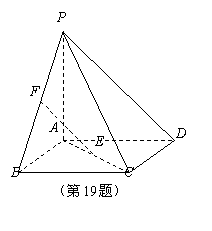 (19) (本题满分14分) 如图, 四棱锥P-ABCD的底面
(19) (本题满分14分) 如图, 四棱锥P-ABCD的底面
ABCD是正方形, PA⊥底面ABCD, E, F分别是
AC, PB的中点.
(Ⅰ) 证明: EF∥平面PCD;
(Ⅱ) 若PA=AB, 求EF与平面PAC所成角的大小.
(20) (本题满分14分) 设数列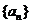 的首项
的首项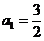 , 前n项和为Sn , 且满足
, 前n项和为Sn , 且满足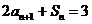
( n∈N*) .
(Ⅰ) 求a2及an ;
(Ⅱ) 求满足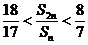 的所有n的值.
的所有n的值.
(21)(本题满分15分)  已知函数
已知函数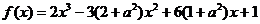 (a∈R).
(a∈R).
(Ⅰ) 若函数f (x)在R上单调, 求a的值;
(Ⅱ) 若函数f (x)在区间[0,2]上的最大值是5, 求a的取值范围.
(22)(本题满分15分)  已知抛物线C的顶点在原点,
焦点为F(0, 1).
已知抛物线C的顶点在原点,
焦点为F(0, 1).
(Ⅰ) 求抛物线C的方程;
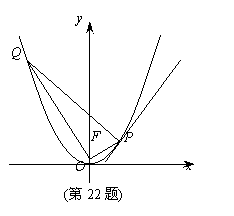 (Ⅱ) 在抛物线C上是否存在点P,
使得过点P的直线交C于另一点Q,
满足
(Ⅱ) 在抛物线C上是否存在点P,
使得过点P的直线交C于另一点Q,
满足
PF⊥QF, 且PQ与C在点P处的切线垂直? 若存在, 求出点P的坐标;
若不存在,请说明理由.
(11) 已知等差数列{an}的前n项和Sn满足: Sn=n2+2n+a(n∈N*), 则实数a=________.
(12) 在平面直角坐标系xOy中, 二元一次方程Ax+By=0(A, B不同时为0)表示过原点的直线. 类比以上结论有: 在空间直角坐标系Oxyz中, 三元一次方程Ax+By+Cz=0(A, B, C不同时为0)表示________.
(13) 若实数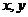 满足不等式组
满足不等式组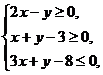 则3x-y的最小值是________.
则3x-y的最小值是________.
 (14) 在1, 2, 3, 4, 5这5个自然数中,
任取2个数, 它们的积是偶数的概率是________.
(14) 在1, 2, 3, 4, 5这5个自然数中,
任取2个数, 它们的积是偶数的概率是________.
(15) 设直线3x+4y-5=0与圆C1: 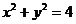 交于A, B两点,
交于A, B两点,
若圆C2的圆心在线段AB上, 且圆C2与圆C1相切, 切点在
圆C1的劣弧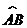 上, 则圆C2的半径的最大值是________.
上, 则圆C2的半径的最大值是________.
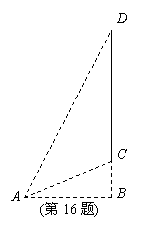
(16) 如图, 某城市的电视发射塔CD建在市郊的小山上, 小山的高
BC为35米, 在地面上有一点A, 测得A, C间的距离为91米,
从A观测电视发射塔CD的视角(∠CAD)为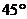 , 则这座电视
, 则这座电视
发射塔的高度CD为________米.
(17) 若对于任意的x∈[1,3], x2+(1-a)x-a+2≥0恒成立, 则实数a的取值范围
是________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com