6．甲是一种能生活在多种土壤中的小型昆虫，常被昆虫乙大量捕食，DDT和aldrin是用于控制这些生物的杀虫剂，aldrin对甲和乙毒性相同，但DDT对乙的毒性比对甲更强，现用DDT和aldrin单独处理田块，如图所示中的哪两个图能分别代表DDT和aldrin单独作用时对昆虫数量的影响(　　 )

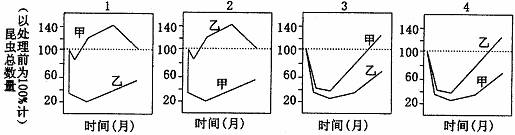
A．2和1　　 　　　 B．1和3 　　 C．2和4　　 　　　 D．3和4

5．老鼠的皮毛黄色(A)对灰色(a)为显性。有一位遗传学家，在实验中发现含显性基因(A)的精子和显性基因(A)的卵细胞不能结合。如果杂合的黄鼠与黄鼠(第一代)交配得到第二代，后代(第二代)相同基因型老鼠继续交配一次得到第三代，那么在第三代中黄鼠的比例为(假定每对老鼠产生的后代数量相同)　

　 A．40%　　　　　　 B．44.4%　　　　　 C．66.7%　　　　　 D．75%

4．下图1表示细胞分裂的不同时期与每条染色体DNA含量变化的关系；图2表示处于细胞分裂不同时期的细胞图象。分析两图，相关的叙述中，都不正确的选项组合是D

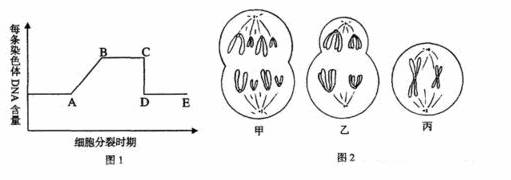
①图1中AB段形成的原因是DNA复制，该过程发生在细胞分裂间期

②图1中CD段形成的原因是着丝点分裂

③图2中甲和乙细胞处于图1中的BC段，图2中丙细胞处于图1的DE段

④图2的甲细胞中染色体数与DNA分子数之比为1∶2

⑤就图2乙分析可知，该细胞含有8条染色单体

⑥图2丙细胞如果是乙细胞的子细胞，那么丙细胞就是次级卵母细胞

A．①②⑤　　　　　　　　　 B．①④⑥　　　　　　　　　 C．②⑤⑥　　　　　　　　　 D．③④⑥

[答案]D

[解析]图1中纵坐标为每条染色体DNA含量变化，其中AB段表示有丝分裂间期或第一间期，BC段表示有丝分裂前中期或减数第一次分裂和减数第二次分裂的前中时期，DE段表示丝分裂后末期及减数减数第二次分裂的后末期。图2的甲表示有丝分裂后期处于图1的DE段，乙图表示减数第一次分裂后期，处于图1的BC段，图2中丙细胞为减数第二次分裂中期，处于图1的BC段。图2的甲细胞中染色体数与DNA分子数之比为1∶1，图2丙细胞如果是乙细胞的子细胞，那么丙细胞是次级卵母细胞或第一极体。

3．位于人体内的神经元的功能分段，以下面模式图表示。下列据图分析的叙述中，正确的是(　　 )

A．突触一般不含有 I 部位的结构

B．一旦Ⅱ部位发生冲动，传导到Ⅳ 部位，就能引发Ⅳ释放兴奋性神经递质

C．III部位传导兴奋时，兴奋部位膜内外电流方向相反

D．神经元的细胞核一般存在于Ⅳ部位

2．右图所示种群在理想环境中呈“J”型增长，在有环境阻力条件下呈“S”型增长。下列有关种群数量增长曲线及其应用的叙述中正确的是(　 )　

A.种群“S”型增长过程中，增长率逐渐增大

B.渔业捕捞后应该控制剩余量在b点

C.种群增长过程中出现环境阻力是在d点之后

D.建立自然保护区，提高K值是保护大熊猫的根本措施

[答案]D

[解析]种群“S”型增长过程中，增长率先逐渐增大后下降；种群增长过程中出现环境阻力是在c点之后；渔业捕捞后需控制剩余量在K/2，即c点。

1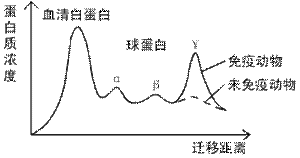．血清蛋白电泳后得到血清白蛋白和三种球蛋白(右图)，据图分析，抗体应属于(　　 )

A．血清白蛋白

B．α球蛋白

C．β球蛋白

D．γ球蛋白

21.(本小题满分13分)

给出定义在(0，+∞)上的三个函数：，，，已知在x＝1处取极值.

(Ⅰ)确定函数h(x)的单调性；

(Ⅱ)求证：当时，恒有成立；

(Ⅲ)把函数h(x)的图象向上平移6个单位得到函数h₁(x)的图象，试确定函数y＝g(x)－h₁(x)的零点个数，并说明理由.

[解](Ⅰ)由题设，，则.　　　　　　　　　　　 (1分)

由已知，，即.　　　　　　　　　　　　　　　　　　　 (2分)

于是，则.　　　　　　　　　　　　　　　　　　　　 (3分)

由，所以h(x)在(1，+∞)上是增函数，在(0，1)上是减函数.(4分)

(Ⅱ)当时，，即.　　　　　　　　　　　　　　 (5分)

欲证，只需证，即证.　　　　　 (6分)

设，则.

当时，，所以在区间(1，e²)上为增函数.　　　　　　　　　 (7分)

从而当时，，即，故.　　　　 (8分)

(Ⅲ)由题设，.令，则

，即.　　　　　　　　　　 (9分)

设，，则

，由，得x＞4.

所以在(4，+∞)上是增函数，在(0，4)上是减函数.　　　　　　　　　　　　 (10分)

又在(0，)上是增函数，在(，+∞)上是减函数.

因为当x→0时，，.

又，，，

，则函数与的大致图象如下：　　　　　　　　　　　　　　 (12分)

由图可知，当x＞0时，两个函数图象有2个交点，故函数y＝g(x)－h₁(x)有2个零点.(13分)

20.(本小题满分13分)

过圆上一点A(4，6)作圆的一条动弦AB，点P为弦AB的中点.

(Ⅰ)求点P的轨迹方程；

(Ⅱ)设点P关于点D(9，0)的对称点为E，O为坐标原点，将线段OP绕原点O依逆时针方向旋转90°后，所得线段为OF，求|EF|的取值范围.

[解](Ⅰ)连结PC，由垂径分弦定理知，PC⊥AB，所以点P的轨迹是以线段AC为直径的圆(除去点A).　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (2分)

因为点A(4，6)，C(6，4)，则其中点坐标为(5，5)，又圆半径.

故点P的轨迹方程是(x≠4，y≠6).　　　　　　　　　　　　　 (5分)

(Ⅱ)因为点P、E关于点D(9，0)对称，设点，则点.　　　　　 (6分)

设点，因为线段OF由OP绕原点逆时针旋转得到，

则OF⊥OP，且|OF|＝|OP|，即

，且.

由，得.令，

则，所以t＝1.

因此点F的坐标为. 　　　　　　　　　　　　　　　　　　　(8分)

所以.

设点M(9，－9)，则.　　　　　　　　　　　　　　　　　　　　 (10分)

因为点P为圆上的点，设圆心为N(5，5)，则

，

.　　　　　　　　　　　　　　　　　　　　　 (12分)

故|EF|的取值范围是.　　　　　　　　　　　　　　　　　 (13分)

19.(本小题满分13分)

某县为了贯彻落实党中央国务院关于农村医疗保险(简称“医保”)政策，制定了如下实施方案：2009年底通过农民个人投保和政府财政投入，共集资1000万元作为全县农村医保基金，从2010年起，每年报销农民的医保费都为上一年底医保基金余额的10%，并且每年底县财政再向医保基金注资m万元(m为正常数).

(Ⅰ)以2009年为第一年，求第n年底该县农村医保基金有多少万元？

(Ⅱ)根据该县农村人口数量和财政状况，县政府决定每年年底的医保基金要逐年增加，同时不超过1500万元，求每年新增医保基金m(单位：万元)应控制在什么范围内.

[解](Ⅰ)设第n年底该县农村医保基金为a_n万元，则

，，即.　　　　　　 (3分)

于是. 所以，

即.　　　　　　　　　　　　　　　　　　　　　　 (6分)

故第n年底该县农村医保基金有万元.　　　　　　　　　 (7分)

(Ⅱ)若每年年底的医保基金逐年增加，则数列单调递增.

因为是减函数，则1000－10m＜0时，即m＞100.　　　　　　　　　　　 (10分)

又恒成立，则.

即10m≤1500，所以m≤150.　　　　　　　　　　　　　　　　　　　　　　　　　 (12分)

故每年新增医保基金m的控制范围是(100，150].　　　　　　　　　　　　　　　　 (13分)

18.(本小题满分12分)

如图，PC⊥平面ABC，PM∥CB，∠ACB＝120°，PM＝AC＝1，BC＝2，异面直线AM与直线PC所成的角为60°.

(Ⅰ)求二面角M－AC－B大小的正切值；

(Ⅱ)求三棱锥P－MAC的体积.

[解]方法一：(Ⅰ)取BC的中点N，连结MN.

由已知，PMCN，则MNPC，所以MN⊥平面ABC.　　　　　　　　　　　　　　 (1分)

过点N作NH⊥AC，交AC的延长线于H，连结MH，

由三垂线定理知，AC⊥MH.

所以∠MHN为二面角M－AC－B的平面角.　　　　　　　　　　　　　　　　　　　 (3分)

连结AN，在△ACN中，由余弦定理，得.

由已知∠AMN＝60°，在Rt△ANM中，.　　　　　　　　　　　　 (6分)

在Rt△CHN中，.　　　　　　　　　　　　　　　　　　　 (7分)

在Rt△MNH中，.

故二面角M－AC－B的正切值是.　　　　　　　　　　　　　　　　　　　　　 (8分)

(Ⅱ)因为四边形PCNM为正方形，MN⊥平面ABC，则

.　　　　　 (12分)

方法二：(Ⅰ)在平面ABC内，过点C作CB的垂线，

按如图所示建立空间直角坐标系.　　　　　　　　　　　　　　　　　　　 (1分)

设点，由已知可得，点，

，则.

因为直线AM与直线PC所成的角为60°，则

，即.

解得z₀＝1，从而.　　　　　　　　　　　　　　　 (3分)

设平面MAC的一个法向量为n，则，即.

取，则n.　　　　　　　　　　　　　　　　　　　　　　　　 (5分)

又m＝(0，0，1)为平面ABC的一个法向量，设向量m与n的夹角为θ，则.

从而，.　　　　　　　　　　　　　　　　　　　　　　　 (7分)

显然，二面角M－AC－B的平面角为锐角，故二面角M－AC－B的正切值是.　　 (8分)

(Ⅱ)因为a＝(1，0，0)为平面PCM的一个法向量，，则

点A到平面PCM的距离.　　　　　　　　　　　　　　　　　　　 (10分)

又PC＝PM＝1，则.　　　 (12分)