
1.已知集合A = {x|–1≤x≤1,x∈N},B = {–1,0,1},集合C满足A∪C = B,则集合C的个数是( )
A.1 B.4 C.7 D.8
21. 解:(1) 是增函数,
是增函数, 当
当 时,
时, 为增函数,又
为增函数,又 为偶函数,
为偶函数, ,
, .
.
当 时,
时,


综上, ………………………………………………5分
………………………………………………5分
(2)当 时,有
时,有 ,
,
当 时,
时, 即
即 ,
, ,
,
当 时,同理,
时,同理, ,
,
同样地, 及
及 ,得
,得

由 的存在性可知,上述不等式在
的存在性可知,上述不等式在 上必有解.
上必有解.
∵ 在
在 上的最小值为
上的最小值为 ,
, ,即
,即 ①
①
令 ,
, .
.
则 由
由 得
得
当 时,
时, ,
, 是减函数;当
是减函数;当 时,
时, ,
, 是增函数
是增函数
∴ 的最小值是
的最小值是 ,又
,又 ,
, ,
,
 ,
,
 在
在
 上有唯一解
上有唯一解 .……10分
.……10分
当 时,
时, ,当
,当 时,
时,
 在
在 时满足不等式①的最大实数解为
时满足不等式①的最大实数解为 ……13分
……13分
当 ,
, 时,
时, ,在
,在 时,
时,

 ,在
,在 时,
时,

综上所述, 最大整数为4. ……13分
最大整数为4. ……13分
20. 解:(1)当 时,
时,








 ……4分
……4分
(2)

 单调递增
单调递增 

又
 综上
综上 ……9分
……9分
(3)


 ………………………………………………13分
………………………………………………13分
19. 解:(1)当 时,
时, ,设所求圆的圆心坐标为
,设所求圆的圆心坐标为
 圆心
圆心 ,到直线
,到直线 的距离为
的距离为 ,则
,则


 ……………………………………6分
……………………………………6分
(2)圆心 关于
关于 的对称点为
的对称点为
 点
点 到
到 的距离为
的距离为
即


 ……………………………………………………………………12分
……………………………………………………………………12分
18.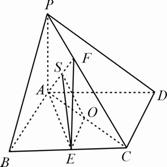 解:(1)
解:(1) 四边形
四边形 为菱形,
为菱形,

 为正三角形.
为正三角形.

 为
为 中点,
中点,
 . 又
. 又 .
. 
 面
面


 面
面 ,
, 面
面
 .
.
(2)设 ,
, 面
面 .
.  为
为 与平面
与平面 所成的角,
所成的角, 中,
中, .
. 当
当 最短时,
最短时, 最大,
最大, ,
, ,
, .
. .
.
过 作
作 于
于 ,则
,则 面
面 ,过
,过 作
作
 于
于 ,连结
,连结 ,则
,则 为二面角的平面角.
为二面角的平面角.  ………………………………12分
………………………………12分
17.解:(1) ,
, ,
, ,
, =3…………………………………………6分
=3…………………………………………6分
(2)
16.解:(1)
 ……………………………………6分
……………………………………6分
(2) ,
,
 ,
,  .
.
 ……………………………………12分
……………………………………12分
14.
 15. ①②③
15. ①②③
9.5,2 10.
假 11.

 12.
12.
 13.
2或
13.
2或
1.A 2. B 3. D 4. D 5. D 6. C 7. C 8. B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com