4、下列各句中，加点的成语使用不恰当的一句是　　　　 (　　 )

　　　 A．美军坦克进入巴格达的时候，伊拉克的武装力量几乎放弃了抵抗；几天后，萨达姆平时最信任的贴身保镖和护卫也大多作鸟兽散。

　　　 B．有人开玩笑说：“犹太金融资本家在豪宅客厅里打个喷嚏，世界上不少银行都将连锁感冒。”这可不是骇人听闻，他们在全球政治经济领域的作用确实非常之大。

　　　 C．健全国内的反腐倡廉机制是有效阻止贪官外逃的治本之策，而一味希图靠外力拿办贪官则是舍本逐末，断不可取。

　　　 D．台湾民进党上台以来，提出的经济举措名目繁多，“拼经济”拼得人们眼花缭乱，但定睛一看，这不过是为推行“台独”而造势罢了。

3]市人大常委会秘书处及时　　 各区县分会场代表的质询意见，分门别类送交各主管委员会负责人。

　　　 A．撤回　 消耗 　收集 B．撤消　 消耗　 搜集

　　　 C．撤回　 消费　 搜集 D．撤消　 消费　 收集

2]这是一条公理：财富只能毁灭崇高的理想和善良的气质，倘若它只　　 在个人的利益上面。

1]因为需要对举证再进行科学论证，为罹患“海湾战争综合症”的退役士兵提供法律援

　助的律师团希望原告暂时　　　 诉讼。

3、依次填入横线处的词语，恰当的一组是　　　　　　　　　 (　　 )

2、下列句子中，没有错别字的一项是　　　　　　　　　 (　　 )

　　　 A．慧星　　 收讫　　 挺而走险　　 振聋发馈

　　　 B．汇编　　 狙击　　 急公好义　　 彪炳春秋

　　　 C．踌躇 　　逼仄　　 既往不纠　　 纵横捭阖

　　　 D．潦倒　　 棉密　　 励精图治　　 敝帚自珍

1、下列各组词语中加点的字的读音，完全相同的一组是　　　　　　 (　　 )

　　　 A．悄寂　　 讥诮　　 春寒料峭　　 行情走俏

　　　 B．憧憬　　 冲压　　 忧心忡忡　　 首当其冲

　　　 C．当今　　 当权　　 螳臂当车　　 罚不当罪

　　　 D．差距　　 差劲　　 差可告慰　　 差强人意

例2 　求函数的值域

错解：令则

　　　 　，　　　　 　　　　(1)

关于t的方程(1)应有实数解，得，即

原因分析：应用 只保证方程(1)在实数范围 内有解，而本题要求方程(1)是在[-1,1]内有解。上面解法忽略了。

正解:令则[-1，1]，

当时[-1，1]；

　当时，=0　　　　　 (2)

　设若在[-1,1]内有一解，则且若(2)在[-1，1]有两解，则得综上所述为求值域

对策：在初中经常说错的话是“某方程无解”正确的说法是“方程无实数解”，在高中方程的解的情况常与范围有关，特别是隐含的范围，求值域若用判别式法，要考虑方程在什么范围内有解。

例3 　求函数的值域

错解：由 得

　　　　　 (*)

　，当　 时， 　　不满足原方程 ,取不到.

原因分析：(1)判别式大于或等于零只能使(*)有实数解，而原方程 要求有大于1的实数解。

(2)对进行平方时产生了增根。与不同解。

正确解法：令　 则

时

对策：求值域一般跟据函数的类型，选用不同的求法，判别式法常用在如的类型 。含有根号的函数一般用换元法。

三 　判定函数奇偶性中的错误

例4 ：判断函数的奇偶性

错解：而是奇函数，是奇函数。

原因分析：一个函数是奇函数还是偶函数的必要条件是定义域关于原点对称。若不对称，则为非奇非偶函数。上题错解是因为：一是不考虑定义域 ，二是原函数与不是同一函数。

正确解法：由得的定义域 为{∣或}它不是关于原点对称的区间，所以为非奇非偶函数

防错对策：函数的奇偶性是在整个定义域内的性质，判断函数的奇偶性必先看定义域是否关于原点对称，小心 错误，如　 是一个奇函数。

四 学习函数单调性中的错误

(1) 认识概念的误区：误认为单调性一定在整个定义域内考虑，实际上单调性是指定义域中某个区间内的性质，这个区间可能是定义域 ，也可能不是。

例5：求函数的单调区间

错解 ：设，且，则　　　　　　　　 (*)

因为不能确定它的符号，所以，无单调区间。

原因分析：在整个定义域内不能定它的符号，但是在较小的区间内可以定它的符号。

正确解法：(*)式的符号由确定，当［-1，1］时函数递增，和都递减。

对策：判定或证明单调性要注意步骤，也要注意区间，有时要分成小区间讨论。同时上式也不能写成在上递减。

(2)复合函数单调性的判定

例6 　求函数㏒的单调区间

错解：令㏒，因为㏒在上是减函数，

在上是减函数，在是增函数。

所以 函数㏒在上是减函数，在上是增函数原因分析：未注意

正确解法：由已知得 且在上是减函数，在上是增函数，所以，函数㏒在上是增函数，在是减函数。

对策：求函数的单调性，方法这里不讲，特别注意函数的定义域 M与函数的值域 D之间的关系是DM

(3)“组合函数”中的问题

从函数与的单调性，不能完全确定+,　　 /, 不要想当然地用某些未证明的结

例如在R上都是增函数，但是，+=在R是增函数，=在R 是减函数，=与/=在R 上不能确定。因此，这问题必须具体问题具体分析。

五 求函数周期性中的问题

1 学习定义的误区：一方面是对定义的理解不透，二方面是误认为只有三角函数才是周期函数

　 例7　 设是定义在R上的偶函数，其图象关于直线对称，对任意，都有

　 (1)设求　 (2) 证明是周期函数

错解：有的学生认为没有哪个三角函数满足，不会证明。这些学生认为只有三角函数才是周期函，因为在三角函数部分才讲周期性。

有的学生错解：因为函数图象关于对称，且是偶函数，得 ，所以函数是周期函数T=2。

原因分析：周期定义中的，是定义域中的任意一个数，这里取持殊值 。

正确解法：因为函数的图象关于直线对称，所以 　　　又　　 所以是R 上的周期函数，且2是它的一个周期。

对策：一定要彻底理解周期的定义，对周期性与对称性的关系参看相关文章的论述。

2、求最小正周期的误区　　　　　　　　　　　　　　　　　　　　　　　　

例8 求函数 的最小正周期

错解：因为函数与函数的最小正周期都是p ，因此，函数的最小正周期是p 。

原因分析：乱用一些没证明的结论。

正确解法：因为　 所以 它的最小正期为。

对策：按大纲要求，只要“了解周期函数和最小正周期的意义，会求函数的周期，或者经过简单的恒等变形可化为上述函数的三角函数的周期”就可以了。不要乱用没证明的结论

许多同学在学习函数这一内容时，只注意记住函数的解析式，会运用函数的一些性质，对函数的三要素(定义、值域、解析式)，只抓住一个要素，因此，在解题中错误百出。特别是定义域 ，在任何时侯都不要忘记，否则，将出许多错误。

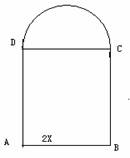
例1如图，用长为的铁丝弯成下部为矩形，上部为半圆形的框架，若矩形的一边长为2,求此框架围成的封闭图形的面积与的函数关系。

错解：由题意得　　　　　　　　　　　　　　　　　

y＝ +　　　　　　　　　　　　　　　

　 =

　 =

原因分析：本题写的是函数关系，因此，还要写出它的定义域 ，由得。补上定义域就对了。

对策：在解函数题 时一定要注意定义域 ，特别在解应用题时，定义域还与实际问题有关。有的同学只考虑解析式有意义的范围，这是不对的。

11、一活塞将一定质量的理想气体封闭在水平固定放置的气缸内，开始时气体体积为V₀，温度为 27⁰C．在活塞上施加压力，将气体体积压缩到2 V₀/3，温度升高到 57⁰C．设大气压强P₀＝l.0×10⁵pa，活塞与气缸壁摩擦不计．

(1)求此时气体的压强；

(2)保持温度不变，缓慢减小施加在活塞上的压力使气体体积恢复到 V_O，求此时气体的压强．

(06上海卷)[答案](1)1.65×10⁵pa (2)1.1×10⁵pa