
6.经市场调查,某商品在近100天内,其销售量和价格均为时间t的函数,且销售量近似地满足关系g(t)=-t+,(t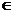 N,0<t≤100),在前40天里价格为f(t)=t+22(t
N,0<t≤100),在前40天里价格为f(t)=t+22(t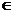 N,0<t≤40),在后60天里价格为f(t)=-t+52(t
N,0<t≤40),在后60天里价格为f(t)=-t+52(t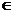 N,40<t≤1
N,40<t≤1 00),求这种商品的日销售额的最大值.
00),求这种商品的日销售额的最大值.
解析:由题意知,当0<t≤40,h(t)=-(t-10.5)2+;
当40<t≤100,h(t)=(t-106.5)2-;∴t=10或11时,这种商品的日销售额的最大值为808.5.
第30、31课时 函数模型及其应用
[例1]一家报刊推销员从报社买进报纸的价格是每份0.20元,卖出的价格是每份0.30元,卖不完的还可以以每份0.08元的价格退回报社.在一个月(以30天计算)有20天每天可卖出400份,其余10天只能卖250份,但每天从报社买进报纸的份数都相同,问应该从报社买多少份才能使每月所获得的利润最大?并计算每月最多能赚多少钱?
[例2]某人从A地到B地乘坐出租车,有两种方案,第一种方案:租用起步价10元,每km价为1.2元的汽车;第二种方案:租用起步价为8元,每km价为1.4元的汽车,按出租车管理条例,在起步价内,不同型号行驶的里程是相等的.则此人从A地到扫地选择哪一种方案比较合适.
[例3]按复利计算利率的储蓄,银行整存一年,年息8%,零存每月利息2%,现把2万元存入银行3年半,求取出后本利的和
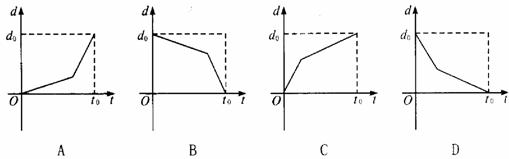
[例4]某学生离家去学校,为了锻炼身体,一开始跑步前进,跑累了再走余下的路,下图中,纵轴表示离学校的距离,横轴表示出发后的时间,则下列四个图形中较符合该生走法的是( )
[例5]容器中有浓度为m%的溶液a升,现从中倒出b升后用水加满,再倒出b升后用水加满,求这样进行了10次后溶液的浓度
[例6]某地方政府为保护地方电子工业发展,决定对某一进口电子产品征收附加税.已知这种电子产品国内市场零售价为每件250元,每年可销售40万件,若政府增加附加税率为每百元收t元时,则每年销售量将减少 t万件.
(1)将税金收入表示为征收附加税率的函数;
(2)若在该项经营中每年征收附加税金不低于600万元,那么附加税率应控制在什么范围?
[例7]将进货单价为8元的商品按10元一个销售,每天可卖出100个.若每个销售涨价一元 ,则日销售量减少10个.为获得最大利润,则此商品当日销售价应定为每个多少元?
,则日销售量减少10个.为获得最大利润,则此商品当日销售价应定为每个多少元?
[例8]为保护环境,实现城市绿化,某房地产公司要在拆迁地矩形ABCD(如下图所示)上规划出一块矩形地面建造住宅区小公园POCR(公园的两边分别落在BC和CD上),但不能超过文物保护三角形AEF的红线EF.问如何设计才能使公园占地面积最大?并求出最大面积.已知AB=CD=200m,BC=AD=160m,AE=60m,AF=40m.
课后练习
5.某商场在促销期间规定:商场内所有商品按标价的80%出售,同时当顾客在该商场内消费满一定金额后,按以下方案获得相应金额的奖券:
|
消费金额的范围 |
[200,400) |
[400,500) |
[500,700) |
[700,900) |
… |
|
获得奖券的金额 |
30 |
60 |
100 |
130 |
… |
根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如:购买标价400元的商品,则消费金额为320元,获得的优惠额为400×0.2+30=110元,设购买商品的优惠率=.
试问:(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在[500,800]内的商品,顾客购买标价为多少元的商品,可获得不小于的优惠率?
答案:(1)优惠率为33%;
(2)标价在[625,750]内的商品,购买时可获得不小于的优惠率.
4.一家人(父亲、母亲、孩子)去某地旅游,有两个旅行社同时发出邀请,且有各自的优惠政策.甲旅行社承诺,如果父亲买一张全票,则其家庭成员均可享受半价,乙旅行社承诺,家庭旅行算团体票,按原价的计算,这两家旅行社的原价是一样的,若家庭中孩子数不同,试分 别列出两家旅行社优惠政策实施后的孩子个数为变量的收费表达式,比较选择哪家更
别列出两家旅行社优惠政策实施后的孩子个数为变量的收费表达式,比较选择哪家更 优惠?
优惠?
解答:设两家旅行社的原价为a(a>0),家庭孩子个数为x(x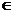 N*),甲、乙两家旅行收费分别为f(x)和g(x),
N*),甲、乙两家旅行收费分别为f(x)和g(x),
则f(x)=a+(x+1)·=x+a(x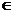 N*),
N*),
g(x)=(x+2)·=x+(x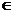 N*),
N*),
g(x)≥f(x),得 x+≤x+,∴x≥1.
因此,当家庭只有1个孩子时,两家随便选择,当孩子数多于1个时,应选择甲旅行社.
2.某纯净水制造厂在净化水的过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,则至少需要过滤的次数为( )(参考数据lg2=0.3010,lg3=0.4771)
A.5 B.10 C.14 D.15
答案:C
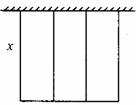 3.有一批材料可以建成200m的围墙,如果用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如下图所示),则围成的矩形最大面积为________m2(围墙厚度不计).
3.有一批材料可以建成200m的围墙,如果用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如下图所示),则围成的矩形最大面积为________m2(围墙厚度不计).
解析:设矩形宽为xm,则矩形长为(200-4x)m,
则矩形面积为
S=x(200-4x)=-4(x-25)2+2500(0<x<50),
∴x=25时,S有最大值2500m2.
1.某城市出租汽车统一价格,凡上车起步价为6元,行程不超过2km者均按此价收费,行程超过2km,按1.8元/km收费,另外,遇到塞车或等候时,汽车虽没有行驶,仍按6分钟折算1km计算,陈先生坐了一趟这种出租车,车费17元,车上仪表显示等候时间为11分30秒,那么陈先生此趟行程介于( )
A.5-7km B.9-11km C.7-9km D.3-5km
答案:A
1.在引入自变量建立目标函数解决函数应用题时,一是要注意自变量的取值范围,二是要检验所得结果,必要时运用估算和近似计算,以使结果符合实际问题的要求. 2.在实际问题向数学问题的转化过程中,要充分使用数学语言,如引入字母,列表,画图,建立坐标系等,以使实际问题数学符号化. 3.对于建立的各种数学模型,要能够模型识别,充分利用数学方法加以解决,并能积累一定数量的典型的函数模型,这是顺利解决实际问题的重要资本.
本节内容主要是运用所学的函数知识去解决实际问题,要求学生掌握函数应用的基本方法和步骤.函数的应用问题是高考中的热点内容,必须下功夫练好基本功.本节涉及的函数模型有:一次函数、二次函数、分段函数及较简单的指数函数和对数函数.其中,最重要的是二次函数模型.
[例7]将进货单价为8元的商品按10元一个销售,每天可卖出100个.若每个销售涨价一元,则日销 售量减少10个.为获得最大利润,则此商品当日销售价应定为每个多少元?
售量减少10个.为获得最大利润,则此商品当日销售价应定为每个多少元?
解析:设每个涨价x元,则实际销售价为(10+x)元,销售的个数为(100-10x),则利润为y=(10+x)(100-10x)-8(100-10x)=-10(x-4)2+360(0≤x≤10).
因此x=4,即售价定为每个14元时,利润最大.
[例8]为保护环境,实现城市绿化,某房地产公司要在拆迁地矩形ABCD(如下图所示)上规划出一块矩形地面建造住宅区小公园POCR(公园的两边分别落在BC和CD上),但不能超过文物保护三角形AEF的红线EF.问如何设计才能使公园占地面积最大?并求出最大面积.已知AB=CD=200m,BC=AD=160m,AE=60m,AF=40m.
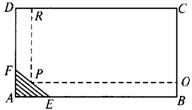 解析:设PO=x,
解析:设PO=x,
则S=-(x-190)2+×1902,0<x<200,
即x=190时,最大面积为24067m2.
总结:
解决函数应用题的流程图是:
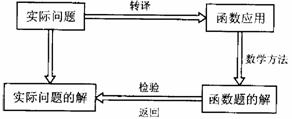
解决函数应用题的基本步骤是:
第一步:认真读题,缜密审题,确切理解题意,明确问题实际背景,然后进行科学的抽象、概括,将实际问 题转化成实际问题,即实际问题数学化.
题转化成实际问题,即实际问题数学化.
第二步:运用所学的数学知识和数学方法解答函数问题,得出函数问题的解.
第三步:将所得函数问题的解代入实际问题进行验证,看是否符合实际,并对实际问题作答.
课后练习
13.某工厂现有甲种原料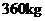 ,乙种原料
,乙种原料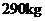 ,计划利用这两种原料生产
,计划利用这两种原料生产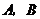 两种产品共
两种产品共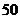 件.已知生产一件
件.已知生产一件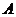 产品,需要甲种原料共
产品,需要甲种原料共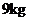 ,乙种原料
,乙种原料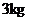 ,可获利润
,可获利润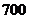 元;生产一件
元;生产一件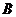 种产品,需用甲种原料
种产品,需用甲种原料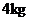 ,乙种原料
,乙种原料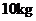 ,可获利润
,可获利润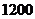 元.
元.
(1)按要求安排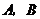 两种产品的生产件数,有几种方案?请你设计出来.
两种产品的生产件数,有几种方案?请你设计出来.
(2)设生产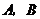 两种产品获总利润
两种产品获总利润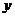 (元),其中一种的生产件数为
(元),其中一种的生产件数为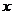 ,试写出
,试写出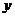 与
与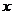 之间的函数关系式,并利用函数性质说明(1)中哪种方案获利最大?最大利
之间的函数关系式,并利用函数性质说明(1)中哪种方案获利最大?最大利 润是多少?
润是多少?
解:(1)设安排生产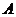 种产品
种产品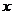 件,则生产
件,则生产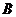 件产品为
件产品为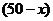 件,依题意,得
件,依题意,得
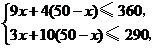
解得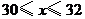 .
.
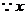 是整数,
是整数,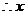 只能取
只能取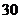 ,
,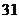 ,
,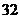 .
.
 生产方案有3种,分别为
生产方案有3种,分别为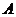 种
种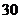 件
件 ,
,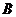 种
种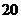 件;
件;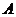 种
种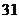 件,
件,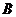 种
种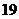 件;
件;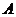 种
种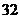 件,
件,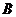 种
种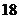 件.
件.
(2)设生产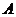 种产品
种产品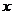 件,则
件,则
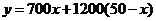
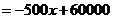 .
.
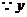 随
随
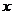 的增大而减小.
的增大而减小.
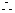 当
当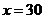 时,
时,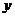 值最大,
值最大,
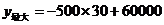
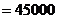 .
.
 安排生产
安排生产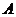
 种产品
种产品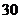 件,
件,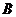 种产品
种产品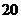 件时,获利最大,最大利润是
件时,获利最大,最大利润是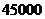 元.
元.
12.某城市现有人口总数为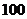 万人,如果年自然增长率为
万人,如果年自然增长率为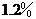 ,试解答下面的问题:
,试解答下面的问题:
(1)写出该城市人口总数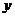 (万人)与经过年数
(万人)与经过年数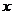 (年)的函数关系式.
(年)的函数关系式.
(2)计算大约多少年后该城市人口将达到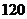 万人(精确到1年).
万人(精确到1年).
解:(1)1年后该城市人口总数为
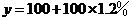
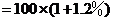 ;
;
2年后该城市人口总数为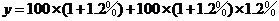
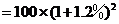 ;
;
3年后该城市人口总数为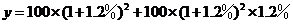
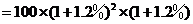
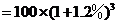 ;
;
……
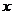 年后该城市人口总数为
年后该城市人口总数为
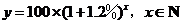 .
.
(2)设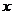 年后该城市人口将达到
年后该城市人口将达到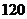 万人,
万人,
即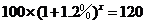 .
.
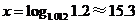 (年),
(年),
即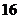 年后该城市人口将达到
年后该城市人口将达到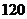 万人.
万人.
11.某自来水厂的蓄水池中有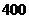 吨水,每天零点开始向居民供水,同时以每小时
吨水,每天零点开始向居民供水,同时以每小时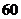 吨的速度向池中注水.已知
吨的速度向池中注水.已知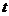 小时内向居民供水总量为
小时内向居民供水总量为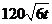 吨
吨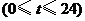 ,问
,问
(1)每天几点时蓄水池中的存水量最少?
(2)若池中存水量不多于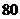 吨时,就会出现供水紧张现象,则每天会有几个
吨时,就会出现供水紧张现象,则每天会有几个 小时出现这种现象?
小时出现这种现象?
解:(1)设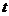 点时(即从零点起
点时(即从零点起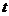 小时后)池中的存水量为
小时后)池中的存水量为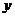 吨,则
吨,则
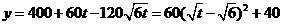 ,
,
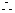 当
当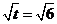 时,即
时,即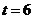 时,
时,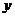 取得最小值
取得最小值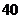 .
.
即每天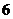 点时蓄水池中的存水量最少.
点时蓄水池中的存水量最少.
(2)由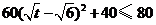 ,
,
解得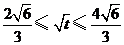 ,
,
即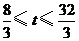 ,
,
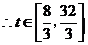 时,池中存水量将不多于
时,池中存水量将不多于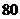 吨,
吨,
由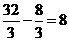 知,每天将有
知,每天将有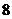 个小时出现供水紧张现象.
个小时出现供水紧张现象.
10.某工厂8年来某产品的总 产量
产量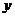 与时间
与时间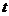 (年)的函数关系如图3所示,则
(年)的函数关系如图3所示,则
①前3年总产量增长速度越来越快;
②前3年总产量增长速度越来越慢;
③第3年后,这种产品停止生产;
④第3年后,这种产品年产量持续增长.
上述说法中正确的是 
 .
.
答案:①③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com