
2、函数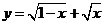 的定义域为( )
的定义域为( )
A.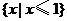 B.
B.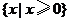 C.
C.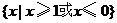 D.
D.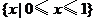
1、满足条件M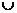 {1}={1,2,3}的集合M的个数是 ( )
{1}={1,2,3}的集合M的个数是 ( )
A.1 B.2 C.3 D.4
22.有一批数量很大的产品,其次品率是10%。
(1)连续抽取两件产品,求两件产品均为正品的概率;
(2)对这批产品进行抽查,每次抽出一件,如果抽出次品,则抽查终止,否则继续抽查,直到抽出次品,但抽查次数最多不超过4次,求抽查次数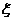 的分布列及期望。
的分布列及期望。
21.有甲、乙、丙三种产品,每种产品的测试合格率分别为0.8,0.8和0.6,从三种产品中各抽取一件进行检验。
(1)求恰有两件合格的概率;
(2)求至少有两件不合格的概率。
20.学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设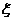 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且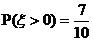 .
.
(1) 求文娱队的人数;
(2) 写出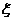 的概率分布列并计算
的概率分布列并计算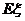 .
.
19.某射手在一次射击中命中9环的概率是0.28,命中8环的概率是0.19,不够8环的概率是0.29,计算这个射手在一次射击中命中9环或10环(最高环数)的概率.
18.将一个半径适当的小球放入如图所示的容 器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入
器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入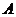 袋或
袋或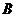 袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是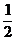 .
.
(1)求小球落入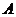 袋中的概率
袋中的概率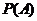 ;
;
(2)在容器入口处依次放入4个小球,记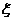 为落入
为落入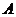
袋中小球的个数,试求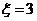 的概率和
的概率和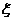 的数学期望
的数学期望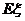 .
.
17.某商场举行抽奖活动,从装有编号0,1,2,3四个小球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖.
(1)求中三等奖的概率;
(2)求中奖的概率.
16.甲、乙两人进行摸球游戏,一袋中装有2个黑球和1个红球。规则如下:若一方摸中红球,将此球放入袋中,此人继续摸球;若一方没有摸到红球,将摸到的球放入袋中,则由对方摸彩球。现甲进行第一次摸球。
(1)在前三次摸球中,甲恰好摸中一次红球的所有情况;
(2)在前四次摸球中,甲恰好摸中两次红球的概率;
(3)设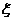 是前三次摸球中,甲摸到的红球的次数,
是前三次摸球中,甲摸到的红球的次数,
求随机变量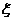 的概率分布与期望.
的概率分布与期望.
15.将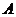 、
、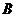 两枚骰子各抛掷一次,观察向上的点数,问:
两枚骰子各抛掷一次,观察向上的点数,问:
(1)共有多少种不同的结果?
(2)两数之和是3的倍数的结果有多少种?
(3)两数之和是3的倍数的概率是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com