2．把一些基本数据、常用公式、重要定理“过过电影”。

1．清点一下用具是否带全(笔、橡皮、作图工具、准考证、手表等)。

高考要取得好成绩，首先要有扎实的基础知识、熟练的基本技能和在长年累月的刻苦钻研中培养起来的数学能力，同时，也取决于临场的发挥，高考的特点是以学生解题能力的高低为标准的一次性选拔，这就使得临场发挥显得尤为重要，研究和总结临场解题策略，进行应试训练和心理辅导，已成为高考辅导的重要内容之一，正确运用数学高考临场解题策略，不仅可以预防各种心理障碍造成的不合理丢分和计算失误及笔误，而且能运用科学的检索方法，建立神经联系，挖掘思维和知识的潜能，考出最佳成绩。

1、提前进入“角色”

高考前一个晚上睡足八个小时，吃好清淡早餐，按清单带齐一切用具，提前半小时到达考区，一方面可以消除新异刺激，稳定情绪，从容进场，另一方面也留有时间提前进入“角色”--让大脑开始简单的数学活动，进入单一的数学情境。如：

16．已知两点M(-1，0)，N(1，0)且点P使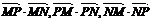成公差小于零的等差数列，

　　 (Ⅰ)点P的轨迹是什么曲线？

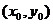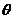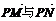　　 (Ⅱ)若点P坐标为，为的夹角，求tanθ．

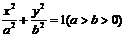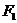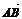15．已知椭圆的长、短轴端点分别为A、B，从此椭圆上一点M向x轴作垂线，恰好通过椭圆的左焦点，向量与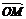是共线向量．

　　 (1)求椭圆的离心率e；

　　 (2)设Q是椭圆上任意一点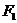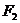， 、分别是左、右焦点，求∠ 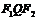的取值范围；

14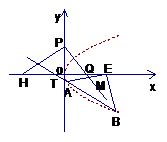．已知点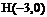，点P在y轴上，点Q在x轴的正半轴上，点M在直线PQ上，且满足，，

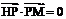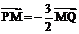(1)当点P在y轴上移动时，求点M的轨迹C；

(2)过点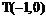作直线m与轨迹C交于A、B两点，若在x轴上存在一点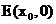，使得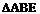为等边三角形，求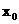的值.

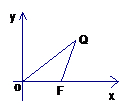13．已知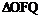的面积为S，且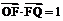，建立如图所示坐标系，

(1)若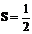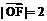，，求直线FQ的方程；

(2)设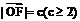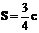，，若以O为中心，F为焦点的椭圆过点Q，求当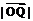取得最小值时的椭圆方程.

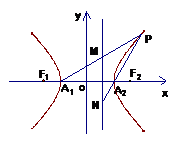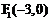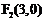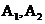12．如图，，是双曲线C的两焦点，直线是双曲线C的右准线， 是双曲线C的两个顶点，点P是双曲线C右支上异于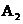的一动点，直线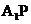、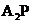交双曲线C的右准线分别于M,N两点，

(1)求双曲线C的方程；

(2)求证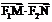：是定值.

11．已知两点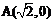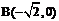，，动点P在y轴上的射影为Q，，

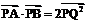　 (1)求动点P的轨迹E的方程；

　 (2)设直线m过点A，斜率为k，当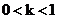时，曲线E的上支上有且仅有一点C到直线m的距离为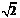，试求k的值及此时点C的坐标.

10．给出下列命题：

　 ①圆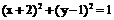关于点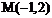对称的圆的方程是；

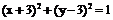②双曲线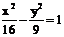右支上一点P到左准线的距离为18，那么该点到右焦点的距离为；

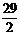③顶点在原点，对称轴是坐标轴，且经过点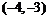的抛物线方程只能是；

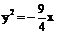④P、Q是椭圆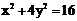上的两个动点，O为原点，直线OP,OQ的斜率之积为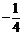，则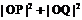等于定值20 .

把你认为正确的命题的序号填在横线上_________________ .