1.掌握平面的基本性质，空间两条直线、直线和平面、两个平面的位置关系(特别是平行和垂直关系)以及它们所成的角与距离的概念.

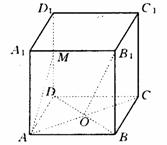
24、在正方体ABCD-A₁B₁C₁D₁中，O为正方形ABCD的中心，M为D₁D的中点.

(I)求证：异面直线B₁O与AM垂直；

(II)求二面角B₁-AM-C的大小；

(III)若正方体的棱长为a，求三棱锥B₁-AMC的体积。(9分)

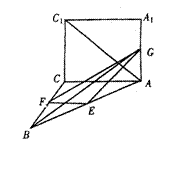
23、如图，正方形ACC₁A₁与等腰直角△ACB互相垂直，∠ACB=90°，E、F分别是AB、BC的中点， G是AA₁上的点.

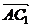
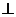
(I)若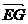，试确定点G的位置；

(II)在满足条件(1)的情况下，试求cos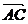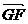＜，＞的值.(8分)

22、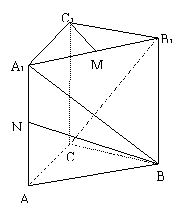如图，直三棱柱ABC-A₁B₁C₁，底面△ABC中，CA=CB=1，∠BCA=90º，

棱AA₁=2，M、N分别是A₁B₁，A₁A的中点，

(I)求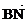的长；

(II)求cos<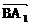,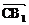>的值；

(III)求证：A₁B⊥C₁M.(9分)

21、球面上三点A、B、C组成这个球的一个截面的内接三角形，AB=18，BC=24，

AC=30，且球心到该截面的距离为球半径的一半。

(1)求球的表面积；

(2)求A，C两点的球面距离。(8分)

20、在正方体ABCD─A₁B₁C₁D₁中，M、N、P分别是A₁B₁，BB₁，B₁C₁的中点，用空间向量的坐标运算证明：B₁D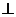平面PMN。(6分)

19、设空间两个不同的单位向量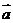=(x₁, y₁ ,0)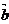，=(x₂, y₂,0)与向量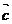=(1,1,1)的夹角都等于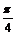，求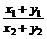的值(6分)

18、一个四面体的所有棱长都是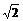，四个顶点在同一个球面上，则此球的表面积为　　　　 ．

17、若棱锥底面面积为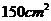，平行于底面的截面面积是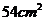，底面和这个截面的距离是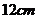，则棱锥的高为　　　　　 ；

16、已知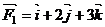,,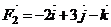 　,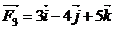若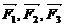共同作用在物体上，使物体从点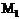(2,-3,2)移到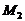(4，2，3)，则合力所作的功　　　　　　　 ；