
7.《华尔街日报》的英文网站网管说,中国文化对全世界的影响将会越来越大,世界上任何一个主流媒体都不可能忽视中国文化的影响。今天,汉文化正在走向世界,在这样的时期,我们更要注意学习唐朝文化的
A.光照四邻,影响深远 B.博大精深,全面辉煌
C.开放探求,兼收并蓄 D.崇尚实用,推陈出新
6.“朝为田舍郎,暮登天子堂”,这一现象反映的历史进步性体现在
A.打破身份限制 公开考试选拔官吏 B.实行乡举里选选拔人才
C.通过察举制自下而上推选人才 D.农民领袖通过起义掌握政权
5.以学习主题统揽历史阶段是学习历史的一个很好的方法。学习主题“封建国家的分裂和民族大融合”统揽的是
A.秦汉时期的历史 B.魏晋南北朝时期
C.隋唐时期的历史 D.明清时期的历史
4.对下列两幅图片相关史实的说明,正确的是

昭君出塞 松赞干布和文成公主入藏
A.前者迫于冒顿单于的威胁,后者是中原王朝主动示好
B.分别促进中原与北部和西南地区经济文化交流
C.分别发生在汉武帝时期和贞观年间
D.都促成中原王朝设置行政机构管辖该地区
3.“中国式建筑是凝固的思想意识形态。……太和殿内皇帝所用的‘御座’,安置在一个高约2米的基座上,使御座从平地升起,犹如须弥座托着太和殿的缩影。”其中突出体现的政治思想是
A.天人感应 B.皇权至上 C.大一统 D.中央集权
2.《左传·昭公》说:“昔武王克殷,成王靖四方,康王息民,并建母弟,以蕃屏周”。材料反映西周的主要政治意图是
A.惠及边民 B.恩及兄弟 C.拱卫周室 D.镇压叛乱
1.《左传》所记春秋时期人们经常把“社稷”一词作为国家政权的代名词。其中“稷”是指
A.土神 B.君主 C.谷神 D.百姓
7.(本题满分18分)本题共有3个小题,第1小题满分4分, 第2小题满分8分, 第3小题满分6分.
在直角坐标平面中,已知点P1(1,2),P2(2,22),┄,Pn(n,2n),其中n是正整数.对平面上任一点A0,记A1为A0关于点P1的对称点, A2为A1关于点P2的对称点, ┄, AN为AN-1关于点PN的对称点.
(1)求向量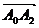 的坐标;
的坐标;
(2)当点A0在曲线C上移动时, 点A2的轨迹是函数y=f(x)的图象,其中f(x)是以3为周期的周期函数,且当x∈(0,3]时,f(x)=lgx.求以曲线C为图象的函数在(1,4]上的解析式;
(3)对任意偶数n,用n表示向量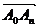 的坐标.
的坐标.
[解](1)设点A0(x,y), A0为P1关于点的对称点A0的坐标为(2-x,4-y),
A1为P2关于点的对称点A2的坐标为(2+x,4+y),
∴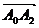 ={2,4}.
={2,4}.
(2) ∵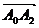 ={2,4},
={2,4},
∴f(x)的图象由曲线C向右平移2个单位,再向上平移4个单位得到.
因此, 曲线C是函数y=g(x)的图象,其中g(x)是以3为周期的周期函数,且当x∈(-2,1]时,g(x)=lg(x+2)-4.于是,当x∈(1,4]时,g(x)=lg(x-1)-4.
另解设点A0(x,y), A2(x2,y2),于是x2-x=2,y2-y=4,
若3< x2≤6,则0< x2-3≤3,于是f(x2)=f(x2-3)=lg(x2-3).
当1< x≤4时, 则3< x2≤6,y+4=lg(x-1).
∴当x∈(1,4]时,g(x)=lg(x-1)-4.
(3)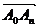 =
=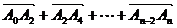 ,
,
由于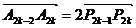 ,得
,得
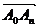 =2(
=2(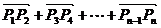 )=2({1,2}+{1,23}+┄+{1,2n-1})=2{
)=2({1,2}+{1,23}+┄+{1,2n-1})=2{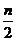 ,
,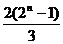 }={n,
}={n,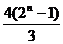 }
}
6.(本题满分16分)本题共有3个小题,第1小题满分4分, 第2小题满分6分, 第3小题满分6分.
对定义域分别是Df、Dg的函数y=f(x) 、y=g(x),
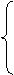 f(x)·g(x) 当x∈Df且x∈Dg
f(x)·g(x) 当x∈Df且x∈Dg
规定: 函数h(x)= f(x)
当x∈Df且x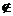 Dg
Dg
g(x) 当x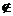 Df且x∈Dg
Df且x∈Dg
(1)
若函数f(x)=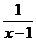 ,g(x)=x2,x∈R,写出函数h(x)的解析式;
,g(x)=x2,x∈R,写出函数h(x)的解析式;
(2) 求问题(1)中函数h(x)的值域;
(3)若g(x)=f(x+α), 其中α是常数,且α∈[0,π],请设计一个定义域为R的函数y=f(x),及一个α的值,使得h(x)=cos4x,并予以证明.
[解] (1)h(x)=
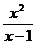 x∈(-∞,1)∪(1,+∞)
x∈(-∞,1)∪(1,+∞)
1 x=1
(2) 当x≠1时, h(x)= 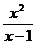 =x-1+
=x-1+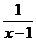 +2,
+2,
若x>1时, 则h(x)≥4,其中等号当x=2时成立
若x<1时, 则h(x)≤ 0,其中等号当x=0时成立
∴函数h(x)的值域是(-∞,0] {1}∪[4,+∞)
(3)令 f(x)=sin2x+cos2x,α=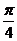
则g(x)=f(x+α)= sin2(x+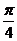 )+cos2(x+
)+cos2(x+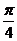 )=cos2x-sin2x,
)=cos2x-sin2x,
于是h(x)= f(x)·f(x+α)= (sin2x+co2sx)( cos2x-sin2x)=cos4x.
另解令f(x)=1+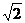 sin2x, α=
sin2x, α=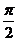 ,
,
g(x)=f(x+α)= 1+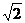 sin2(x+π)=1-
sin2(x+π)=1-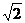 sin2x,
sin2x,
于是h(x)= f(x)·f(x+α)= (1+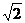 sin2x)( 1-
sin2x)( 1-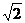 sin2x)=cos4x.
sin2x)=cos4x.
5.已知函数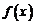 和
和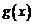 的图象关于原点对称,且
的图象关于原点对称,且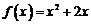 .
.
(Ⅰ)求函数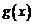 的解析式;
的解析式;
(Ⅱ)解不等式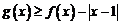 ;
;
(Ⅲ)若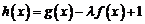 在
在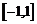 上是增函数,求实数
上是增函数,求实数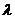 的取值范围.
的取值范围.
本题主要考查函数图象的对称、二次函数的基本性质与不等式的应用等基础知识,以及综合运用所学知识分析和解决问题的能力.满分14分.
解:(Ⅰ)设函数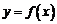 的图象上任意一点
的图象上任意一点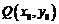 关于原点的对称点为
关于原点的对称点为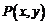 ,则
,则
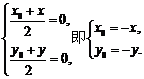
∵点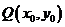 在函数
在函数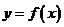 的图象上
的图象上
∴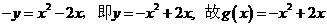
(Ⅱ)由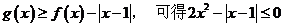
当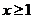 时,
时,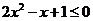 ,此时不等式无解.
,此时不等式无解.
当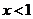 时,
时,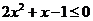 ,解得
,解得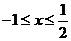 .
.
因此,原不等式的解集为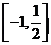 .
.
(Ⅲ)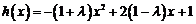
①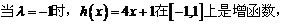
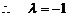
②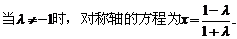
ⅰ)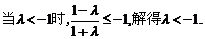
ⅱ)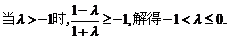
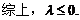
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com