
3. 点关于点的对称点(中点坐标公式)
2. 平行线间的距离公式
1. 点到直线距离公式及证明
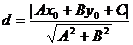
关于证明:
根据点斜式,直线PQ的方程为(不妨设A≠0)
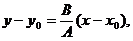
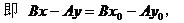
解方程组
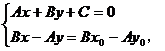
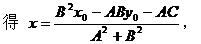
这就是点Q的横坐标,又可得
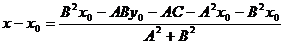
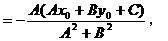
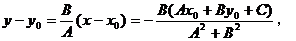
所以,
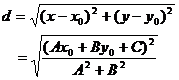
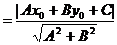 。
。
这就推导得到点P(x0,y0)到直线l:Ax+By+C=0的距离公式。
如果A=0或B=0,上式的距离公式仍然成立。
下面再介绍一种直接用两点间距离公式的推导方法。
设点Q的坐标为(x1,y1),则
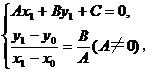
把方程组作变形,
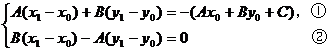
把①,②两边分别平方后相加,得
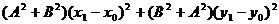
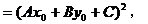
所以,
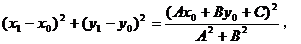
所以,
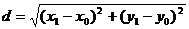
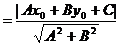
此公式还可以用向量的有关知识推导,介绍如下:
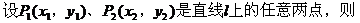
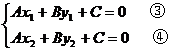
把③、④两式左右两边分别相减,得
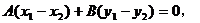
由向量的数量积的知识,知
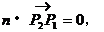
这里n=(A,B)。所以n=(A,B)是与直线l垂直的向量。
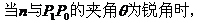
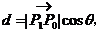
(如图所示)
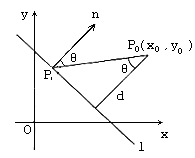

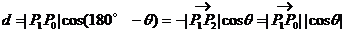
(如图所示)
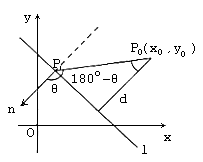
所以,都有
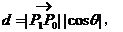
因为
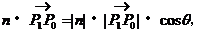
所以
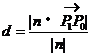
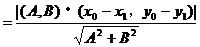
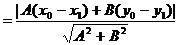
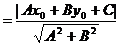
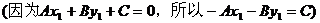
点到直线的距离;
点关于点、关于直线的对称点;
直线关于点、关于直线的对称直线;
直线方程复习;
19. 直线
直线 经过抛物线
经过抛物线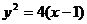 的焦点,且与准线成30
的焦点,且与准线成30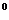 角,则直线
角,则直线 的斜截式方程是
的斜截式方程是
18.已知双曲线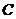 :
: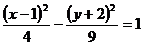 ,给出以下四个命题:
,给出以下四个命题:
① 双曲线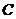 的渐近线方程是
的渐近线方程是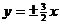 ;
;
② 直线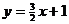 与双曲线
与双曲线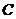 只有一个交点;
只有一个交点;
③ 将双曲线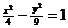 向左平移一个单位,并向上平移两个单位,可以得到双曲线
向左平移一个单位,并向上平移两个单位,可以得到双曲线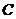 ;
;
④ 双曲线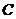 的一个焦点到一条渐近线的距离为3。
的一个焦点到一条渐近线的距离为3。
 其中所有正确命题的序号是
其中所有正确命题的序号是
17.椭圆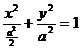 与连结
与连结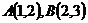 的线段没有公共点,则正数
的线段没有公共点,则正数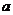 的取值范围是
的取值范围是

16.已知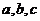 为某一直角三角形的三边,
为某一直角三角形的三边,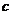 为斜边,若点
为斜边,若点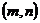 在直线
在直线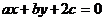 上,则
上,则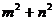 的最小值为
的最小值为

15.直线x-2y-3=0与圆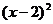 +
+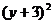 =9交于P、Q两点,则△POQ (O是原点)的面积等于(
)
=9交于P、Q两点,则△POQ (O是原点)的面积等于(
)
(A) 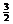 (B)
(B)
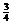
(C) 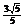 (D)
(D)
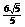
14.已知两点M(0,1).N(10,1)给出下列直线方程:
① 5x-3y-22=0 ② 5x-3y-52=0
③ x-y-4=0 ④ 4x-y-14=0
在直线上存在点P满足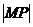 =
=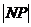 +6的所有直线方程是( )
+6的所有直线方程是( )
(A) ①②③ (B) ②④
(C) ①③ (D) ②③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com