3．抛物线y=ax²+bx+c(a≠0)，若a>0，当x≤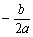时，y随x的增大而减小；当x≥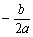时，y随x的增大而增大．若a<0，当x≤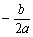时，y随x的增大而增大；当x≥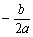时，y随x的增大而减小．

2．抛物线y=ax²+bx+c(a≠0)的图象：当a>0时，开口向上，当a<0时开口向下，对称轴是直线x=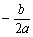，顶点坐标是()．

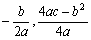1．二次函数y=ax²，y=a(x-h)²，y=a(x-h)²+k，y=ax²+bx+c(各式中，a≠0)的图象形状相同，只是位置不同，它们的顶点坐标及对称轴如下表：

解析式	y=ax2	y=a(x-h)2	y=a(x-h)2+k	y=ax2+bx+c
顶点坐标	(0，0)	(h，0)	(h，k)	()
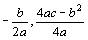对 称 轴	x=0	x=h	x=h	x=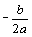

　当h>0时，y=a(x-h)²的图象可由抛物线y=ax²向右平行移动h个单位得到， 　当h<0时，则向左平行移动|h|个单位得到． 　当h>0,k>0时，将抛物线y=ax²向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)²+k的图象； 　当h>0,k<0时，将抛物线y=ax²向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)²+k的图象； 　当h<0,k>0时，将抛物线向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)²+k的图象； 　当h<0,k<0时，将抛物线向左平行移动|h|个单位，再向下移动|k|个单位可得到y=a(x-h)²+k的图象； 　因此，研究抛物线 y=ax²+bx+c(a≠0)的图象，通过配方，将一般式化为y=a(x-h)²+k的形式，可确定其顶点坐标、对称轴，抛物线的大体位置就很清楚了．这给画图象提供了方便．

3．会根据已知图象上三个点的坐标求出二次函数的解析式．

　名师精讲

2．能利用图象或配方法确定抛物线的开口方向及对称轴、顶点的位置．

1．会用描点法画出二次函数的图象．

20．请以“开放在生命深处的花朵”为标题写一篇文章。

要求：1．除诗歌外，文体不限。2．不少于800字。

19．下面是一篇“中国首届全球通手机短信文学大赛”散文类获奖作品，请你为这篇作品写几句评点的话。(80字左右)(5分)

山里的母亲

　 　母亲这辈子只识得三个字，那就是她的名字。母亲这辈子只做一件事，那就是劳动。母亲这辈子只有一个愿望，那就是让三个孩子走出这山。母亲这辈子唯一的欣慰，那就是她的孩子秉承了她的执著和坚韧。

17. 依次填入下面一段文字横线处的语句，衔接最恰当的一组是(3分)

马在漫长的进化历程中的发展趋势是体型从小到大，腿和脚由短变长。　　　　　　

　　　　　　　　　　　　　　　 ，侧趾退化，不再使用，只靠中趾支撑身体，行走和奔跑。

　　 ①所以在演化中四肢逐渐变得长而有力

　　 ②这个发展趋势也反映了马从适应于森林生活到适应草原生活的过程

　　 ③在草原中生活极易受到肉食动物的袭击

　　 ④由于马是被捕食的动物

　　 ⑤而最好的防御方式就是要比捕食它的动物跑得更快

A．③⑤①②④　　　 B．②③④⑤①　　　 C．②④③⑤①　　　 D．②③④①⑤