10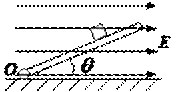．如图所示，质量为m的物体带正电Q在斜面上处于静止状态，物体与斜面均在匀强电场内，匀强电场E方向水平向右。当斜面的倾角θ逐渐增大(θ<90°)，而该带电体仍静止在斜面上时，(　　 )

　 A．物体所受合外力为零。

　 B．物体所受静摩擦力的方向可能会改变180°。

　 C．物体的重力势能逐渐增大，电势能逐渐减小。

　 D．物体的重力势能逐渐增大，电势能逐渐增大。

第Ⅱ卷 ( 非选择题:共70分)

9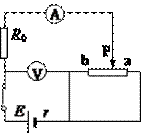．如图所示电路中，电源的电动势为E，内电阻为r，当滑动变阻器的滑片P由a向b滑动的过程中，电流表、电压表的示数变化情况是(　　)

　 A．电流表示数一直减小，电压表示数一直增大

　 B．电流表示数一直增大，电压表示数一直减小

　 C．电流表示数先增大后减小，电压表示数先减小后增大

　 D．电流表示数先减小后增大，电压表示数先增大后减小

8．欧姆在探索通过导体的电流和电压、电阻关系时由于无电源和电流表，他就利用金属在冷水和热水中产生电动势代替电源，用小磁针的偏转检测电流，具体做法是：在地磁场作用下处于水平静止的小磁针上方，平行于小磁针水平放置一直导线，当该导线中通有电流时，小磁针会发生偏转；当通过该导线电流为I时，小磁针偏转了30°，问当他发现小磁针偏转了60°，通过该直导线的电流为(已知直导线在某点产生的磁场与通过直导线的电流成正比(　　 )

　　 　A．2I　　　　　 　 B．I　　　 　C．3I　　　　 　 D． I

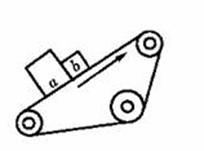
6．在北京机场货物托运处，常用传送带运送行李和货物，　　　　　 如图所示，靠在一起的两个质地相同，质量和大小均不同的包装箱随传送带一起上行，下列说法正确的是　(　　 　 )

　　 A．匀速上行时b受3个力作用

　　 B．匀加速上行时b受4个力作用

　　 C．若上行过程传送带因故突然停止时，b受4个力作用

　　 D．若上行过程传送带因故突然停止后，b受的摩擦力一定比原来大

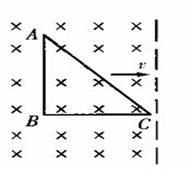　7．如图所示，在垂直纸面向里，磁感应强度为B的匀强磁场区域中有一个均匀导线制成的单匝直角三角形线框。现用外力使线框以恒定的速度v沿垂直磁场方向向右运动，运动中线框的AB边始终与磁场右边界平行，已知AB=BC=L，线框导线的总电阻为R。则线框离开磁场的过程中(　　 )

　　 A．线框中的电动势随时间均匀增大

B．通过线框截面的电荷量为BL²/(2R)

C．线框所受外力的最大值为B²VL²/R

　 D．线框中的热功率与时间成正比

4.举世瞩目的北京2008奥运会上，何雯娜为中国夺得史上首枚蹦床奥运金牌，为祖国争得了荣誉。比赛刚开始，何雯娜要在竖直方向上经过几次高高跃起，某次跃起从最高点至最低点的过程中(忽略空气阻力)，下列正确的是　(　　　 ) 　　

　　　 A．速度先增大后减小至床面时最大　

　　 B．加速度先不变后减小

　　 C．人接触床面后蹦床的弹性势能先增大后减小

　　 D．人、床和地球组成的系统的机械能守恒

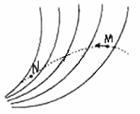　 5．图中的实线表示电场线，虚线表示只受电场力作用的带正电粒子的运动轨迹粒子先经过M点，再经过N点，可以判定(　　 )

　　　 A．M点的电势高于N点的电势

　　　 B．粒子在M点的电势能小于在N点的电势能

　　　 C．粒子在M点动能大于在N点的动能

　　　 D．粒子在M点受到的电场力小于在N点受到的电场力

3．联合国安理会五个常任理事国都拥有否决权，即只要其中一个常任理事国投反对票，提案就不能通过。假设设计一个表决器，常任理事国投反对票时输入“0”，投赞成票或弃权时输入“l”，提案通过输出为“l”，通不过输出为“0”，则这个表决器应具有的逻辑关系是(　　 　)

　 　　A．与门　　 　B．或门　　 　C．非门　　 　D．与非门

1．2008年5月四川汶川大地震发生后，有多名空降兵从近5000m的高空跳伞，安全着陆后及时向指挥员报告灾情。假设空降兵跳伞经历竖直加速下降和竖直减速下降两个过程，将人和伞看成一个系统，在这两个过程中，下列说法正确的是(　　 )

　　 A.系统受到的合外力始终向下

　　 B.运动阻力始终竖直向上

　　 C.系统的重力势能增加

　　 D.在相等的时间内系统下落的位移相等

　2. 为纪念伽利略将望远镜用于天文观测400周年,2009年被定为以“探索我的宇宙”为主题的国际天文年．我国发射的“嫦娥一号”卫星绕月球经过一年多的运行，完成了既定任务，于2009年3月1日16时13分成功撞月．如图为“嫦娥一号” 卫星撞月的模拟图，卫星在控制点1开始进入撞月轨道．假设卫星绕月球作圆周运动的轨道半径为R，周期为T，引力常量为G．根据题中信息，以下说法正确的是( 　　　)

A．可以求出月球的质量　 　　　　　

B．可以求出月球对“嫦娥一号”卫星的引力

C．“嫦娥一号”卫星在控制点1处应减速　 D．“嫦娥一号”在地面的发射速度大于11.2km/s

(1)、(选修4-4：坐标系与参数方程)

在极坐标系中，从极点O作直线与另一直线相交于点M，在OM上取一点P，使．

　 1)求点P的轨迹方程；

　 2)设R为上任意一点，试求RP的最小值．

(2)、 选修4－5：不等式选讲

　 1)(6分) 设均为正数，且，求证

　 2)(6分) 已知、都是正数，且，求证：.

21．(12分)　　　

已知函数

(1) 试判断函数的单调性；

(2) 设，求在上的最大值；

(3)试证明：对，不等式

20、(12分)

已知椭圆C中心在原点、焦点在轴上，椭圆C上的点到焦点的最大值为，最小值为．

　(1)求椭圆C的标准方程；

　(2)若直线：与椭圆交于不同的两点(不是左、右顶点)，且以为直径的圆经过椭圆的右顶点．求证：直线过定点，并求出定点的坐标．