
19.(本小题满分14分)
已知数列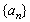 的前
的前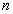 项和
项和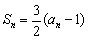 ,
,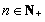 .
.
(1)求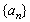 的通项公式;
的通项公式;
(2)若对于任意的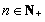 ,有
,有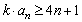 成立,求实数
成立,求实数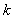 的取值范围.
的取值范围.
18.(本小题满分14分)
已知函数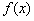 满足
满足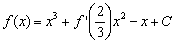 (其中
(其中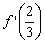 为
为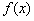 在点
在点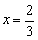 处的导数,
处的导数,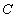 为常数).
为常数).
(1)求函数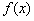 的单调区间;
的单调区间;
(2)若方程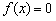 有且只有两个不等的实数根,求常数
有且只有两个不等的实数根,求常数 .
.
17.(本小题满分12分)
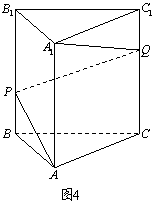 如图4,正三棱柱
如图4,正三棱柱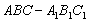 中,
中,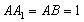 ,
,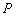 、
、 分别是侧棱
分别是侧棱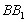 、
、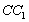 上的三等分点,
上的三等分点,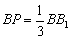 ,
,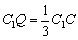 .
.
(1)证明:平面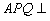 平面
平面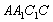 ;
;
(2)求四面体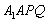 的体积.
的体积.
16.(本小题满分12分)
设有同频率的两个正弦电流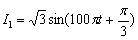 ,
,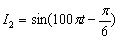 ,把它们合成后,得到电流
,把它们合成后,得到电流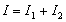 .
.
(1)求电流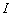 的最小正周期
的最小正周期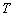 和频率
和频率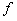 ;
;
(2)设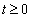 ,求电流
,求电流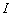 的最大值和最小值,并指出
的最大值和最小值,并指出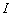 第一次达到最大值和最小值时的
第一次达到最大值和最小值时的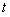 值.
值.
(二)选做题(14-15题,考生只能从中选做一题)
14. (坐标系与参数方程选做题)圆锥曲线
(坐标系与参数方程选做题)圆锥曲线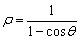 的准线的极坐标方程是 .
的准线的极坐标方程是 .
15.(几何证明选讲选做题)如图3,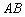 是圆
是圆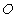 的直径,弦
的直径,弦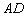
和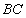 相交于点
相交于点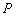 ,且
,且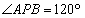 ,则
,则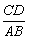 等于
.
等于
.
(一)必做题(11-13)
11.若△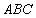 的三个内角满足
的三个内角满足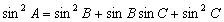 ,则
,则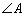 等于 .
等于 .
12.据研究,甲、乙两个磁盘受到病毒感染,感染的量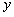 (单位:比特数)与时间
(单位:比特数)与时间 (单位:秒)的函数关系式分别是
(单位:秒)的函数关系式分别是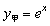 和
和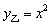 .
.
显然,当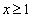 时,甲磁盘受到的病毒感染增长率比乙磁盘受到的病毒感染增长率大.试根据上述事实提炼一个不等式是
.
时,甲磁盘受到的病毒感染增长率比乙磁盘受到的病毒感染增长率大.试根据上述事实提炼一个不等式是
.
13.给出下列四个命题:
①设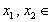 R,则
R,则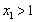 且
且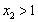 的充要条件是
的充要条件是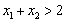 且
且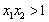 ;
;
②任意的锐角三角形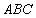 中,有
中,有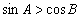 成立;
成立;
③平面上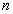 个圆最多将平面分成
个圆最多将平面分成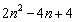 个部分;
个部分;
④空间中直角在一个平面上的正投影可以是钝角.
其中真命题的序号是 (要求写出所有真命题的序号).
10. 已知点
已知点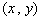 所在的可行域如图2所示.若要使目标函数
所在的可行域如图2所示.若要使目标函数
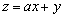 取得最大值的最优解有无数多个,则
取得最大值的最优解有无数多个,则 的值为
的值为
A.4
B.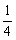 C.
C.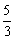 D.
D.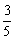
9.若偶函数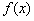 在
在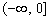 内单调递减,则不等式
内单调递减,则不等式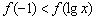 的解集是
的解集是
A.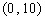 B.
B.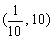 C.
C.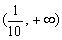 D.
D.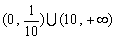
8.如果二次方程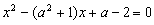 有一个根比1大,另一个根比
有一个根比1大,另一个根比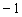 小,则实数
小,则实数 的取值范围是
的取值范围是
A.( ,1) B.(
,1) B.(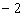 ,0) C.(
,0) C.(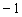 ,0) D.(0,2)
,0) D.(0,2)
7.已知向量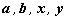 满足
满足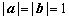 ,
,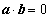 ,且
,且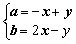 ,则
,则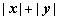 等于
等于
A.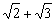 B.
B.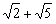 C.
C.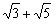 D.7
D.7
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com