
2.数形结合思想。解题时重视方程的几何意义和图形的辅助作用是非常必要的。即:将对几何图形的研究,转化为对代数式的研究,同时又要理解代数问题的几何意义。
[例题解析]
例1 已知圆(x+4)2+y2=25的圆心为M1,圆(x-4)2+y2=1的圆心为M2,一动圆与这两个圆都外切。
(1)求动圆圆心P的轨迹方程;
(2)若过点M2的直线与(1)中所求轨迹有两个交点A、B,求|AM1|·|BM1|的取值范围。
解 (1)∵|PM1|-5=|PM2|-1,∴|PM1| - |PM2|=4
∴动圆圆心P的轨迹是以M1、M2为焦点的双曲线的右支。
c=4,a=2,b2=12,
故所求轨迹方程为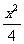 -
-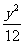 =1(x≥2)。
=1(x≥2)。
(2)当过M2的直线倾斜角不等于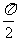 时,设其斜率为k,
时,设其斜率为k,
直线方程为 y=k(x-4)
与双曲线 3x2-y2-12=0联立,消去y化简得
(3-k2)x2+8k2x-16k2-12=0
又设A(x1,y1),B(x2,y2),x1>0,x2>0
由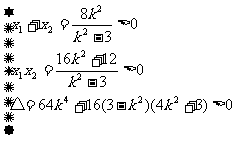
解得 k2>3。
由双曲线左准线方程 x=-1且e=2,有
|AM1|·|BM1|=e|x1+1|·e|x2+1|
=4[x1x2+(x1+x2)+1]
=4(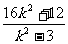 +
+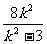 +1)
+1)
=100+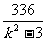
∵k2-3>0,∴|AM1|×|BM1|>100
又当直线倾斜角等于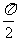 时,A(4,y1),B(4,y2),
时,A(4,y1),B(4,y2),
|AM1|=|BM1|=e(4+1)=10
|AM1|·|BM1|=100
故 |AM1|·|BM1|≥100。
例2 如图9-1,已知圆C:(x+4)2+y2=4。圆D的圆心D在y轴上且与圆C外切。圆 D与y轴交于A、B两点,点P为(-3,0)。
(1)若点D坐标为(0,3),求∠APB的正切值;
(2)当点D在y轴上运动时,求∠APB的最大值;
(3)在x轴上是否存在定点Q,当圆D在y轴上运动时,∠AQB是定值?如果存在,求出点Q坐标;如果不存在,说明理由。
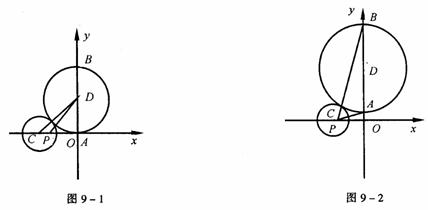
解 (1)∵|CD|=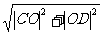 =5,(O为原点)且圆D与圆C外切,
=5,(O为原点)且圆D与圆C外切,
∴圆D半径r=5-2=3,
此时,A、B坐标分别为(0,0)、(0,6),
∴PA在x轴上,且BP的斜率k=2,
∴tan∠APB=2。
(2)如图9-2,设D的坐标为(0,a),圆D的半径为r,则(r+2)2=16+a2。 ①
设PA、PB的斜率为k1、k2,又A、B的坐标分别为(0,a-r)、(0,a+r)。则
k1=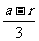 ,k2=
,k2=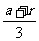 ,
,
∴tan∠APB=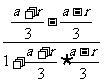 =
= ②
②
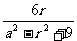
由①解出a2代入②,得tan∠APB=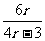 =
=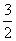 +
+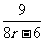 ,而8r-6为单调增函数,r∈[2,+∞
,而8r-6为单调增函数,r∈[2,+∞ 。
。
∴tan∠APB∈(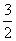 ,
,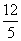
∠APB的最大值为arttan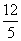 。
。
(3)假设存在Q点,设Q(b,0),QA、QB的斜率分别为k1,k2,则k1=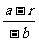 ,k2=
,k2=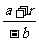 ,
,
tan∠AQB=|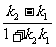 |=|
|=|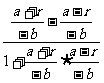 |=|
|=| |
|
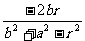
将a2=(r+2)2 – 16代入上式,得
tan∠AQB=|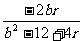 |=|
|=|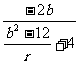 |
|
欲使∠AQB大小与r无关,则应有b2=12,即b=±2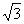 ,
,
此时tan∠AQB=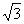 ,∠AQB=60°。
,∠AQB=60°。
∴存在Q点,当圆D变动时,∠AQB为定值60°,这Q点坐标为(±2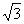 ,0)。
,0)。
例3 设正方形ABCD(A、B、C、D顺时针排列)的外接圆方程为x2+y2-6x+a=0(a<9),C、D点所在直线l的斜率为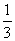 。
。
(1)求外接圆圆心M点的坐标及正方形对角线AC、BD的斜率;
(2)如果在x轴上方的A、B两点在一条以原点为顶点,以x轴为对称轴的抛物线上,求此抛物线的方程及直线l的方程;
(3)如果ABCD的外接圆半径为2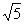 ,在x轴上方的A、B两点在一条以x轴为对称轴的抛物线上,求此抛物线的方程及直线l的方程。
,在x轴上方的A、B两点在一条以x轴为对称轴的抛物线上,求此抛物线的方程及直线l的方程。
解 (1)由(x-3)2+y2=9-a(a<9)可知圆心M的坐标为(3,0),依题意:
∠ABM=∠BAM=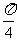 ,kAB=
,kAB=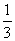 。
。
∴MA,MB的斜率k满足:|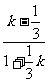 |=1,
|=1,
解得:kAC= -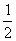 ,kBD=2。
,kBD=2。
(2)设MB、MA的倾斜角分别为θ1、θ2,则tanθ1=2,tanθ2= -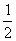 ,
,
可以推出:cosθ1=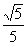 , sinθ1=
, sinθ1=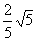 ,cosθ2= -
,cosθ2= -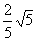 ,sinθ2=
,sinθ2=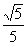 。
。
再设|MA|=|MB|=r,则A(3-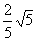 r,
r,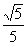 r),B(3+
r),B(3+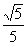 r,
r, 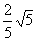 r)。
r)。
设抛物线方程为y2=2px(p>0),由于A,B两点在抛物线上,
∴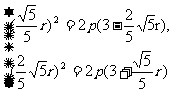
 解出:r=
解出:r=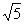 ,p=
,p=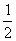 。
。
得抛物线方程为y2=x。
由此可知A点坐标为(1,1),且A点关于M(3,0)的对称点C的坐标是(5,-1),
∴直线l的方程为y -(-1)=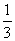 (x-5),
(x-5),
即x-3y-8=0。
(3)将圆方程(x-3)2+y2=(2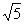 )2分别与AC、BD的直线方程:
)2分别与AC、BD的直线方程:
y= -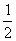 (x-3),y=2(x-3)联立,可解得A(-1,2),B(5,4)。
(x-3),y=2(x-3)联立,可解得A(-1,2),B(5,4)。
设抛物线方程为y2=a(x-m) (*)
将A(-1,2)、B(5,4)的坐标代入(*),得
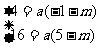
解得:a=2,m= -3,
∴抛物线的方程为y2=2(x+3)。
A(-1,2)点关于M(3,0)的对称点为C(7,-2),
故直线l的方程为y-(-2)=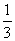 (x-7),即x-3y-13=0。
(x-7),即x-3y-13=0。
例4 如图9-3,已知:射线OA为y=kx(k>0,x>0),射线OB为y= -kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
(1)当k为定值时,动点P的纵坐标y是横坐标x的函数,求这个函数y=f(x)的解析式;
(2)根据k的取值范围,确定y=f(x)的定义域。
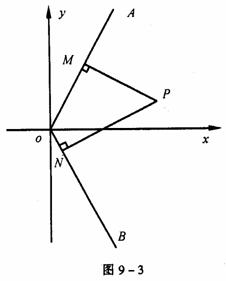
解 (1)设M(a,ka),N(b,-kb),(a>0,b>0)。
则|OM|=a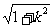 ,|ON|=b
,|ON|=b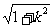 。
。
由动点P在∠AOx的内部,得0<y<kx。
∴|PM|=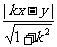 =
=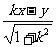 ,|PN |=
,|PN |=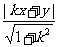 =
=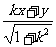
∴S四边形ONPM=S△ONP+S△OPM
=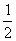 (|OM|·|PM|+|ON|·|PN|)
(|OM|·|PM|+|ON|·|PN|)
=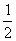 [a(kx-y)+b(kx+y)]
[a(kx-y)+b(kx+y)]
=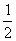 [k(a+b)x -
(a-b)y]=k
[k(a+b)x -
(a-b)y]=k
∴k(a+b)x-(a-b)y=2k ①
又由kPM= -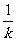 =
=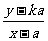 , kPN=
, kPN=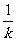 =
=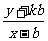 ,
,
分别解得a=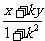 ,b=
,b=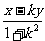 ,
,
代入①式消a、b,并化简得x2-y2=k2+1。
∵y>0,∴y=
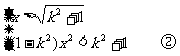
(2)由0<y<kx,得
0< <kx
<kx
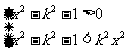
 (*)
(*)
当k=1时,不等式②为0<2恒成立,
∴(*) x>
x>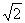 。
。
当0<k<1时,由不等式②得x2<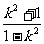 ,x<
,x<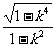 ,
,
∴(*)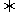
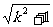 <x<
<x<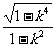 。
。
当k>1时,由不等式②得x2>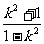 ,且
,且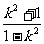 <0,
<0,
∴(*) x>
x>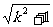
但垂足N必须在射线OB上,否则O、N、P、M四点不能组成四边形,所以还必须满足条件
y<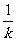 x,将它代入函数解析式,得
x,将它代入函数解析式,得
 <
<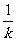 x
x
解得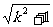 <x<
<x<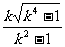 (k>1),或x∈k(0<k≤1)。
(k>1),或x∈k(0<k≤1)。
综上:当k=1时,定义域为{x|x>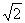 };
};
当0<k<1时,定义域为{x|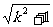 <x<
<x<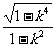 };
};
当k>1时,定义域为{x|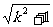 <x<
<x<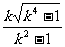 }。
}。
例5 已知函数f(x)=x2-1(x≥1)的图像为C1,曲线C2与C1关于直线y=x对称。
(1)求曲线C2的方程y=g(x);
(2)设函数y=g(x)的定义域为M,x1,x2∈M,且x1≠x2,求证|g(x1)-g(x2)|<|x1-x2|;
(3)设A、B为曲线C2上任意不同两点,证明直线AB与直线y=x必相交。
解 (1)曲线C1和C2关于直线y=x对称,则g(x)为f(x)的反函数。
∵y=x2-1,x2=y+1,又x≥1
∴x=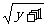
则曲线C2的方程为g(x)= 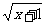 (x≥0)。
(x≥0)。
(2)设x1,x2∈M,且x1≠x2。
则x1-x2≠0。又x1≥0, x2≥0,
∴|g(x1)-g(x2)|=|
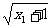 -
-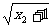 |
|
=
≤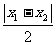 <|x1-x2|
<|x1-x2|
(3)设A(x1,y1)、B(x2,y2)为曲线C2上任意不同两点。
x1,x2∈M,且x1≠x2,
由(2)知,|kAB|=|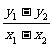 |=
|=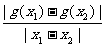 <1
<1
∴直线AB的斜率|kAB|≠1,
又直线y=x的斜率为1,
∴直线AB与直线y=x必相交。
例6 已知⊙O′过定点A(0,p)(p>0),圆心O′在抛物线x2=2py上运动,MN为圆O′截x轴所得的弦,令|AM|=d1,|AN|=d2,∠MAN=θ。
(1)当O′点运动时,|MN|是否有变化?并证明你的结论;
(2)求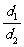 +
+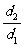 的最大值,并求取得最大值的θ值。
的最大值,并求取得最大值的θ值。
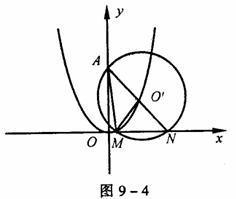
解 (1)设O′(x0,y0),则x02=2py0
(y0≥0),⊙O′的半径|O′A|=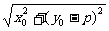 ,⊙O′的方程为(x-x0)2+(y-y0)2=x02+(y0-p)2。令y=0,并把x02=2py0代入得x2-2x0x+x02-p2=0,解得xM=x0 – p,xN=x0+p,∴|MN|=| xN – xM|=2p为定值。
,⊙O′的方程为(x-x0)2+(y-y0)2=x02+(y0-p)2。令y=0,并把x02=2py0代入得x2-2x0x+x02-p2=0,解得xM=x0 – p,xN=x0+p,∴|MN|=| xN – xM|=2p为定值。
(2)∵M(x0-p,0) ,N(x0+p,0) ∴d1=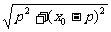 ,d2=
,d2=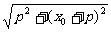 ,则d12+d22=4p2+2x02,d1d2=
,则d12+d22=4p2+2x02,d1d2=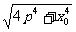 ,∴
,∴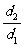 +
+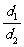 =
=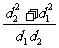 =
=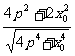 =2
=2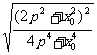 =
=
2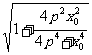 ≤2
≤2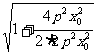 =2
=2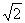
当且仅当x02=2p2,即x=±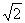 p,y0=p时等号成立,∴
p,y0=p时等号成立,∴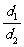 +
+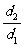 的最大值为2
的最大值为2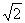 。
。
此时|O′B|=|MB|=|NB|(B为MN中点),又O′M=O′N,
∴△O′MN为等腰直角三角形,∠MO′N=90°,则θ=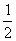 ∠MO′N=45°。
∠MO′N=45°。
例7 已知函数y=log2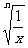 (n∈N)。
(n∈N)。
(1)当n=1,2,3…时,把已知函数的图像和直线y=1的交点的横坐标依次记为a1, a2, a3,…,求证a1+ a2+ a3+…+ an<1;
(2)对于每一个n的值,设A n、B n为已知函数的图像上与x轴距离为1的两点,求证n取任意一个正整数时,以A n B n为直径的圆都与一条定直线相切,并求出这条定直线的方程和切点的坐标。
解 原函数可化为:y=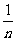 log
log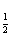 x。
x。
(1)y=1时,可求得x=(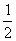 )n,即an=(
)n,即an=(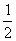 )n=
)n=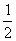 (
(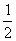 )n-1,
)n-1,
∴{an}是以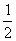 为首项,
为首项,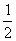 为公比的等比数列。
为公比的等比数列。
∴a1+ a2+ a3+…+ an=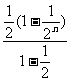 =1-
=1-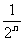 <1
<1
(2)同理可以求An、Bn的横坐标,可得An、Bn的坐标分别为(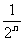 ,1)和(2n,-1),因此| AnBn |=
,1)和(2n,-1),因此| AnBn |=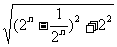 =2n+
=2n+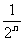 ,
,
因此AnBn中点C到y轴距离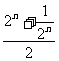 =
=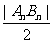 ,
,
∴以C为圆心、AnBn为直径的圆必与定直线y轴相切,这条定直线的方程为x=0。由点C的纵坐标为0,可知从点C到y轴作垂线的垂足就是原点,即切点,所以切点坐标为(0,0))。
例8 自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程。(1989年全国高考数学试题)
解法一 已知圆的标准方程是
(x-2)2+(y-2)2=1,它关于x轴的对称圆的方程是(x-2)2+(y+2)2=1。设光线L所在的直线的方程是y-3=k(x+3)(其中斜率k待定),由题设知对称圆的圆心C′(2,-2)到这条直线的距离等于1,即d=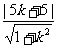 =1。整理得 12k2+25k+12=0,解得k= -
=1。整理得 12k2+25k+12=0,解得k= -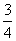 或k= -
或k= -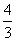 。故所求直线方程是y-3= -
。故所求直线方程是y-3= -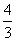 (x+3),或y-3= -
(x+3),或y-3= -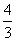 (x+3),即3x+4y+3=0或4x+3y+3=0。
(x+3),即3x+4y+3=0或4x+3y+3=0。
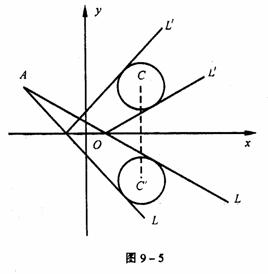
解法二 已知圆的标准方程是(x-2)2+(y-2)2=1,设交线L所在的直线的方程是
y-3=k(x+3)(其中斜率k待定),由题意知k≠0,于是L的反射点的坐标是(-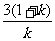 ,0),因为光线的入射角等于反射角,所以反射光线L′所在直线的方程为y=
-k(x+
,0),因为光线的入射角等于反射角,所以反射光线L′所在直线的方程为y=
-k(x+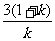 ),即y+kx+3(1+k)=0。这条直线应与已知圆相切,故圆心到直线的距离为1,即d=
),即y+kx+3(1+k)=0。这条直线应与已知圆相切,故圆心到直线的距离为1,即d=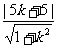 =1。以下同解法一。
=1。以下同解法一。
例9 设圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3∶1,在满足条件①、②的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程。(1997年全国高考数学试题)
解法一 设圆的圆心为P(a,b),半径为r,则点P到x轴,y轴的距离分别为|b|,|a|。由题设知圆P截x轴所得劣弧所对的圆心角为90°,∴圆P截x轴所得的弦长为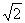 r,故r2=2b2。又圆P截y轴所得的的弦长为2,所以有r2=a2+1。从而得2b2-a2=1。又点P(a,b)到直线x-2y=0的距离为d=
r,故r2=2b2。又圆P截y轴所得的的弦长为2,所以有r2=a2+1。从而得2b2-a2=1。又点P(a,b)到直线x-2y=0的距离为d=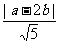 ,所以5d2=|a-2b|2=a2+4b2-4ab≥a2+4b2 -2(a2+b2)=2b2-a2=1,当且仅当a=b时,上式等号成立,从而要使d取得最小值,则应有
,所以5d2=|a-2b|2=a2+4b2-4ab≥a2+4b2 -2(a2+b2)=2b2-a2=1,当且仅当a=b时,上式等号成立,从而要使d取得最小值,则应有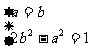 ,解此方程组得
,解此方程组得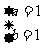 或
或 。又由r2=2b2知r=
。又由r2=2b2知r=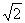 。于是,所求圆的方程是(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2。
。于是,所求圆的方程是(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2。
解法二 同解法一得d=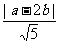 ,∴a-2b=±
,∴a-2b=±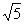 d,得a2=4b2±
d,得a2=4b2±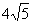 bd+5d2 ①
bd+5d2 ①
将a2=2b2-1代入①式,整理得2b2±4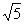 bd+5d2+1=0
② 把它看作b的二次方程,由于方程有实根,故判别式非负,即△=8(5d2-1)≥0,得5d2≥1。所以5d2有最小值1,从而d有最小值
bd+5d2+1=0
② 把它看作b的二次方程,由于方程有实根,故判别式非负,即△=8(5d2-1)≥0,得5d2≥1。所以5d2有最小值1,从而d有最小值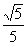 。将其代入②式得2b2±4b+2=0,解得b=±1。将b=±1代入r2=2b2得r2=2,由r2=a2+1得a=±1。综上a=±1,b=±1,r2=2。由|a-2b|=1知a,b同号。于是,所求圆的方程是(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2。
。将其代入②式得2b2±4b+2=0,解得b=±1。将b=±1代入r2=2b2得r2=2,由r2=a2+1得a=±1。综上a=±1,b=±1,r2=2。由|a-2b|=1知a,b同号。于是,所求圆的方程是(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2。
1.公式法。求直线和圆的方程要正确运用公式解题。各种位置关系的判断要灵活使用各种结论。
12.两圆的位置关系的判定方法。
设两圆圆心分别为O1、O2,半径分别为r1,r2,|O1O2|为圆心距,则两圆位置关系如下:
|O1O2|>r1+r2 两圆外离;
两圆外离;
|O1O2|=r1+r2 两圆外切;
两圆外切;
| r1-r2|<|O1O2|< r1+r2 两圆相交;
两圆相交;
| O1O2 |=| r1-r2| 两圆内切;
两圆内切;
0<| O1O2|<| r1-r2| 两圆内含。
两圆内含。
11.直线与圆的位置关系的判定方法。
(1)法一:直线:Ax+By+C=0;圆:x2+y2+Dx+Ey+F=0。
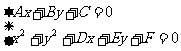
 一元二次方程
一元二次方程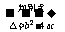

(2)法二:直线:Ax+By+C=0;圆:(x-a)2+(y-b)2=r2,圆心(a,b)到直线的距离为
d=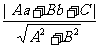


10.确定圆方程需要有三个互相独立的条件。圆的方程有两种形式,要注意各种形式的圆方程的适用范围。
(1)圆的标准方程:(x-a)2+(y-b)2=r2,其中(a,b)是圆心坐标,r是圆的半径;
(2)圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0),圆心坐标为(-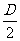 ,-
,-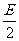 ),半径为r=
),半径为r=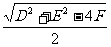 。
。
9.点到直线的距离公式。
(1)已知一点P(x0,y0)及一条直线l:Ax+By+C=0,则点P到直线l的距离d=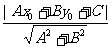 ;
;
(2)两平行直线l1:Ax+By+C1=0, l2:Ax+By+C2=0之间的距离d=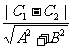 。
。
8.怎么判断两直线是否平行或垂直?判断两直线是否平行或垂直时,若两直线的斜率都存在,可以用斜率的关系来判断;若直线的斜率不存在,则必须用一般式的平行垂直条件来判断。
(1)斜率存在且不重合的两条直线l1∶y=k1x+b1, l2∶y=k2x+b2,有以下结论:
①l1∥l2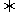 k1=k2
k1=k2
②l1⊥l2 k1·k2= -1
k1·k2= -1
(2)对于直线l1∶A1x+B1y+C1=0, l2∶A2x+B2y+C2=0,当A1,A2,B1,B2都不为零时,有以下结论:
①l1∥l2
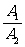 =
=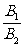 ≠
≠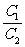
②l1⊥l2 A1A2+B1B2
= 0
A1A2+B1B2
= 0
③l1与l2相交
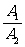 ≠
≠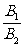
④l1与l2重合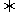
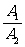 =
=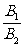 =
=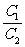
7.两条直线的夹角。当两直线的斜率k1,k2都存在且k1·k2≠ -1时,tanθ=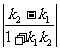 ,当直线的斜率不存在时,可结合图形判断。另外还应注意到:“到角”公式与“夹角”公式的区别。
,当直线的斜率不存在时,可结合图形判断。另外还应注意到:“到角”公式与“夹角”公式的区别。
6.平面上直线与二元一次方程是一一对应的。
5.确定直线方程需要有两个互相独立的条件。确定直线方程的形式很多,但必须注意各种形式的直线方程的适用范围。
|
名称 |
方程 |
说明 |
适用条件 |
|
斜截式 |
y=kx+b |
k--斜率 b--纵截距 |
倾斜角为90°的直线不能用此式 |
|
点斜式 |
y-y0=k(x-x0) |
(x0,y0)--直线上 已知点,k--斜率 |
倾斜角为90°的直线不能用此式 |
|
两点式 |
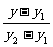 = =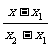 |
(x1,y1),(x2,y2)是直线上两个已知点 |
与两坐标轴平行的直线不能用此式 |
|
截距式 |
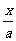 + +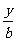 =1 =1 |
a--直线的横截距 b--直线的纵截距 |
过(0,0)及与两坐标轴平行的直线不能用此式 |
|
一般式 |
Ax+By+C=0 |
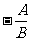 , ,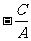 , ,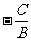 分别为斜率、横截距和纵截距 分别为斜率、横截距和纵截距 |
A、B不能同时为零 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com