
一项是符合题目要求的.
21. (本小题满分13分)对于在区间[m,n]上有意义的两个函数 与
与 ,如果对任意
,如果对任意 [m,n]均有
[m,n]均有 ,称
,称 与
与 在[m,n]上是接近的,否则称
在[m,n]上是接近的,否则称 与
与 在[m,n]上是非接近的,现有两个函数
在[m,n]上是非接近的,现有两个函数 与
与 (a>0,a≠1),给定区间[a+2,a+3].
(a>0,a≠1),给定区间[a+2,a+3].
(1)若 与
与 在给定区间[a+2,a+3]上都有意义,求a的取值范围;
在给定区间[a+2,a+3]上都有意义,求a的取值范围;
(2)讨论 与
与 在[a+2,a+3]上是否是接近的.
在[a+2,a+3]上是否是接近的.
 2010届衡阳市两校联考试卷
2010届衡阳市两校联考试卷
数学(理科)
20. (本小题满分13分)如图,
(本小题满分13分)如图, ,
, 分别是椭圆
分别是椭圆 (a>b>0)的左右焦点,M为椭圆上一点,
(a>b>0)的左右焦点,M为椭圆上一点,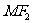 垂直于x轴,且OM与椭圆长轴和短轴端点的连线AB平行。
垂直于x轴,且OM与椭圆长轴和短轴端点的连线AB平行。
(1)求椭圆的离心率;
(2)若G为椭圆上不同于长轴端点任一点,求∠ 取值范围;
取值范围;
(3)过 且与OM垂直的直线交椭圆于P、Q.
且与OM垂直的直线交椭圆于P、Q.
19.(本小题满分13分)设数列 的前
的前 项和为
项和为 ,且
,且 ;数列
;数列 为等差数列,且
为等差数列,且 ,
, .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)若 ,
, 为数列
为数列 的前
的前 项和.
求证:
项和.
求证: .
.
18.(本小题满分12分)某隧道长2150米,通过隧道的车速不能超过20米/秒.一个由55辆车身都为10米的同一车型组成的运输车队匀速通过该隧道.设车队的速度为x米/秒,根据安全和车流的需要,相邻两车均保持 米的距离,其中a为常数且
米的距离,其中a为常数且 ,自第一辆车车头进入隧道至第55辆车车尾离开隧道所用时间为y(秒) .
,自第一辆车车头进入隧道至第55辆车车尾离开隧道所用时间为y(秒) .
(1)将y表示为x的函数;
(2)求车队通过隧道所用时间取最小值时车队的速度.
17、 (本小题满分12分)如图,正方形
(本小题满分12分)如图,正方形 所在的平面与平面
所在的平面与平面 垂直,
垂直,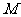 是
是 和
和 的交点,
的交点,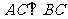 ,且
,且 .
.
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成的角的大小;
所成的角的大小;
(3)求二面角 的大小.
的大小.
16、(本小题满分12分)已知向量 =(sin(
=(sin( +x),
+x), cosx),
cosx),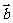 =(sinx,cosx), f(x)=
=(sinx,cosx), f(x)=  ·
·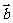 .
.
⑴求f(x)的最小正周期和单调增区间;
⑵如果三角形ABC中,满足f(A)= ,求角A的值.
,求角A的值.
15、在计算“ ”时,某同学学到了如下一种方法:先改写第k项:
”时,某同学学到了如下一种方法:先改写第k项:
 由此得
由此得


… 
相加,得
类比上述方法,请你计算“ ”,其结果为 .
”,其结果为 .
14、给出以下几个命题,正确的是 .
①函数 对称中心是
对称中心是 ;
;
②已知 是等差数列
是等差数列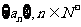 的前n项和 ,若
的前n项和 ,若 ;
;
③函数 为奇函数的充要条件是
为奇函数的充要条件是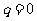 ;
;
④已知 均是正数,且
均是正数,且 ,则
,则 。
。
13、若直线 始终平分圆
始终平分圆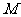 :
: 的周长,则
的周长,则 的最小值为
。
的最小值为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com