
2、对称性:
1、范围:
例1 (1)已知抛物线标准方程是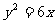 ,则它的焦点坐标为
,则它的焦点坐标为 ,
,
准线 的方程为
的方程为
(2)已知抛物线的焦点坐标是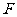 (2,0),则它的标准方程是
(2,0),则它的标准方程是 。
。
(3)已知抛物线的准线方程是x=-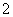 ,则它的标准方程是
,则它的标准方程是 。
。
(4) 点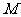 与点
与点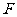 (4,0)的距离和它到直线
(4,0)的距离和它到直线 的距离相等,则点
的距离相等,则点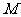 的轨迹方程是_________________
的轨迹方程是_________________
(5)点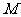 与点
与点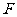 (4,0)的距离比它到直线
(4,0)的距离比它到直线 的距离小1,求点
的距离小1,求点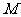 的轨迹方程。
的轨迹方程。
(四)数形结合思考:
在方程 中,因为一次项
中,因为一次项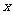 系数为_____,可得到焦点坐标_________,可以说:一次项
系数为_____,可得到焦点坐标_________,可以说:一次项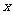 系数是
系数是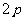 ,则焦点在
,则焦点在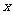 轴上,且焦点的横坐标等于一次项
轴上,且焦点的横坐标等于一次项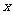 的系数的四分之一,同时也可以得到准线方程___________。反之,如果已知焦点的坐标是
的系数的四分之一,同时也可以得到准线方程___________。反之,如果已知焦点的坐标是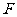 (
(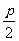 ,0),可以写出,抛物线标准方程____________;同理,如果已知准线方程是
,0),可以写出,抛物线标准方程____________;同理,如果已知准线方程是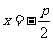 ,也可以写出,抛物线标准方程____________。
,也可以写出,抛物线标准方程____________。
(二) 抛物线的定义
1、定义:平面内与一个定点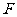 和一条不经过定点
和一条不经过定点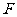 的定直线
的定直线 的距离_____的点的轨迹
的距离_____的点的轨迹
叫做________
定点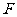 叫做__________,定直线
叫做__________,定直线 叫做_____________
叫做_____________
l
 (三) 探究二:抛物线的标准方程
(三) 探究二:抛物线的标准方程
问题1:坐标系应如何建立,分析下面两方案哪一个更好些?
(1) 以定直线为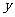 轴,过
轴,过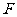 做定直线的垂线为
做定直线的垂线为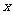 轴;
·F
轴;
·F
(2) 过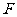 做定直线的垂线为
做定直线的垂线为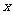 轴,以抛物线与
轴,以抛物线与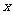 轴交点为原点,
轴交点为原点,
再画出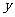 轴
轴
问题2:抛物线的标准方程的推导:
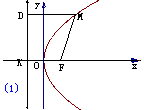
填空:如图所示,取经过点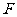 且垂直
且垂直 的直线为
的直线为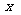 轴,垂足为
轴,垂足为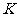 。以
。以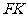 的中点
的中点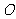 为原点,建立直角坐标系系,设|
为原点,建立直角坐标系系,设|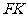 |=
|=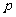 (
(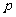 >0),
>0),
那么焦点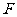 的坐标为______,准线
的坐标为______,准线 的方程为_______________,
的方程为_______________,
设抛物线上的点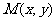 ,动点
,动点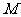 满足的几何条件是______________
满足的几何条件是______________
 则有_____________________
则有_____________________
化简方程得_____________________
方程______________叫做抛物线的标准方程
它表示的抛物线的焦点在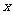 轴的正半轴上,焦点坐标是
轴的正半轴上,焦点坐标是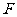 (
(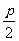 ,0),它的准线方程是
,0),它的准线方程是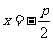 。
。
(一)探究一:抛物线的定义
问题:当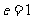 时,在平面内与一定点的距离和
时,在平面内与一定点的距离和
 一条定直线的距离的比是常数
一条定直线的距离的比是常数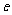 =1的点的轨迹是什么?
=1的点的轨迹是什么?
l
教师演示步骤画图
(1)平面内一个定点F和一条不经过定点F的定直线
(2)在直线 上任取点H,过点H作
上任取点H,过点H作 ·F
·F
(3)作线段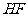 的垂直平分线
的垂直平分线 ,交
,交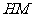 于
于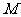
探究思考:当点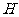 在直线
在直线 上运动时,
上运动时,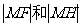 的大小关系?
的大小关系?
你的结论:当点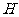 在直线
在直线 上运动时,总有______________,即动点
上运动时,总有______________,即动点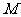 到定点
到定点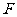 的距离和到定直线
的距离和到定直线 的距离_______
的距离_______
动点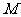 的轨迹是______________
的轨迹是______________
椭圆和双曲线的有共同的几何特征:都可以看作是,在平面内与一定点的距离和一条定直线的距离的比是常数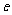 的点的轨迹。(其中定点不在直线上)
的点的轨迹。(其中定点不在直线上)
当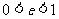 时,轨迹是_______;当
时,轨迹是_______;当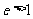 时,轨迹是__________。
时,轨迹是__________。
4. 你对老师的教学有哪些想法,请告诉老师.
3. 你还有哪些地方不清楚的,请告诉老师.
2.你在哪些数学能力上有所提高?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com