
5、已知函数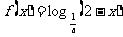 在其定义域上单调递减,则函数
在其定义域上单调递减,则函数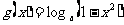 的单调减区间是( )
的单调减区间是( )
A.  B.
B. 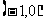 C.
C.
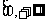 D.
D.
4、将函数 的图象向左平移一个单位得到图象
的图象向左平移一个单位得到图象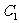 ,再将
,再将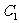 向上平移一个单位得图象
向上平移一个单位得图象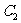 ,作出
,作出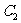 关于直线
关于直线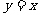 对称的图象
对称的图象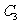 ,则
,则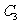 对应的函数的解析式为( )
对应的函数的解析式为( )
A. 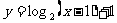 B.
B.
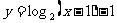
C. 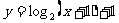 D.
D.
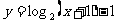
3、已知0< <1,
<1,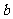 <-1,则函数
<-1,则函数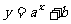 的图象必定不经过( )
的图象必定不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2、已知函数 的定义域为[0,1],值域为[1,2],则函数
的定义域为[0,1],值域为[1,2],则函数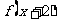 的定义域和值域分别是( )
的定义域和值域分别是( )
A. [0,1] ,[1,2] B. [2,3] ,[3,4] C. [-2,-1] ,[1,2] D. [-1,2] ,[3,4]
1、已知函数 ,
,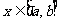 ,那么集合
,那么集合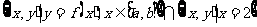 中元素的个数为( )
中元素的个数为( )
A. 1 B. 0 C. 1或0 D. 1或2
22.(本小题12分)
已知函数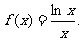
(I)求函数 的 单调区间,并比较
的 单调区间,并比较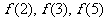 的大小;
的大小;
(II)证明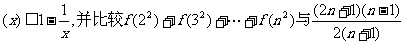 的大小。
的大小。
21.(本小题12分)
已知函数
(I)当a=1时,求 的最小值;
的最小值;
(II)若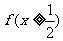 恒成立,求a的取值范围。
恒成立,求a的取值范围。
20.(本小题12分)
在三角形ABC中, AB=2,BC=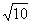 ,CA=3。点M是三角形ABC三边的高所在直线的交点。
,CA=3。点M是三角形ABC三边的高所在直线的交点。
(I)求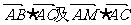 的值;
的值;
(II)求满足关系式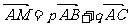 的实数p及q 值。
的实数p及q 值。
19.(本小题12分)
已知递增的等比数列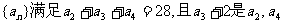 的等差中项。
的等差中项。
(1)求数列 的通项公式;
的通项公式;
(2)若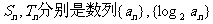 的前n项和,求
的前n项和,求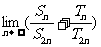 的值。
的值。
18.(本小题12分)
某中学在高一开设了4门选修课,每个学生必须且只需选修1门选修课,对于该年级的甲、乙、丙3名学生,回答下列问题。
(I)求这3名学生选择的选修课互不相同的概率;
(II)求恰有2门选修课没有被这3名学生选择的概率;
(III)某一选修课被这3名学生选择的人数的数学期望。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com