
28.(2009宁夏海南卷理)用min{a,b,c}表示a,b,c三个数中的最小值 ( )
设f(x)=min{, x+2,10-x} (x 0),则f(x)的最大值为
0),则f(x)的最大值为
(A)4 (B)5 (C)6 (D)7
答案 C
27.(2009辽宁卷文)已知偶函数 在区间
在区间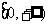 单调增加,则满足
单调增加,则满足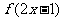 <
<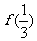 的x 取值范围是 (
)
的x 取值范围是 (
)
(A)(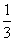 ,
,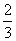 ) B.[
) B.[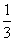 ,
,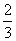 ) C.(
) C.( ,
,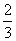 ) D.[
) D.[ ,
,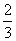 )
)
答案 A
解析 由于f(x)是偶函数,故f(x)=f(|x|)
∴得f(|2x-1|)<f(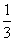 ),再根据f(x)的单调性
),再根据f(x)的单调性
得|2x-1|<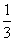 解得
解得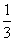 <x<
<x<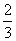
26.(2009福建卷理)函数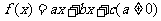 的图象关于直线
的图象关于直线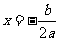 对称。据此可推测,对任意的非零实数a,b,c,m,n,p,关于x的方程
对称。据此可推测,对任意的非零实数a,b,c,m,n,p,关于x的方程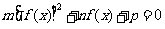 的解集都不可能是 ( )
的解集都不可能是 ( )
A. 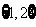 B
B
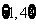 C
C
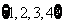 D
D 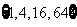
答案 D
解析 本题用特例法解决简洁快速,对方程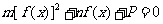 中
中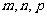 分别赋值求出
分别赋值求出 代入
代入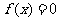 求出检验即得.
求出检验即得.
25.(2009四川卷文)已知函数 是定义在实数集R上的不恒为零的偶函数,且对任意实数
是定义在实数集R上的不恒为零的偶函数,且对任意实数 都有
都有
 ,则
,则 的值是 ( )
的值是 ( )
A. 0
B.  C.
1
D.
C.
1
D. 
答案 A
解析 若 ≠0,则有
≠0,则有 ,取
,取 ,则有:
,则有:
 (∵
(∵ 是偶函数,则
是偶函数,则
 )由此得
)由此得 于是
于是

24..(2009湖北卷理)设球的半径为时间t的函数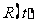 。若球的体积以均匀速度c增长,则球的表面积的增长速度与球半径 ( )
。若球的体积以均匀速度c增长,则球的表面积的增长速度与球半径 ( )
A.成正比,比例系数为C B. 成正比,比例系数为2C
C.成反比,比例系数为C D. 成反比,比例系数为2C
答案 D
解析 由题意可知球的体积为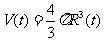 ,则
,则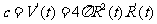 ,由此可
,由此可
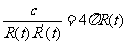 ,而球的表面积为
,而球的表面积为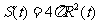 ,
,
所以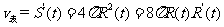 ,
,
即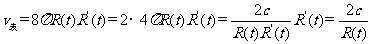 ,故选
,故选
23.(2009湖北卷理)设a为非零实数,函数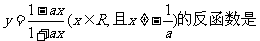 ( )
( )
A、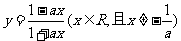 B、
B、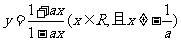
C、 D、
D、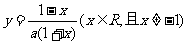
答案 D
解析 由原函数是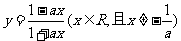 ,从中解得
,从中解得
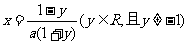 即原函数的反函数是
即原函数的反函数是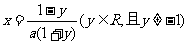 ,故选择D
,故选择D
22.(2009天津卷文)设函数f(x)在R上的导函数为f’(x),且2f(x)+xf’(x)>x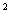 ,x下面的不等式在R内恒成立的是 ( )
,x下面的不等式在R内恒成立的是 ( )
A.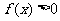 B.
B.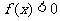 C.
C.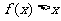 D.
D.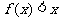
答案 A
解析 由已知,首先令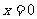 ,排除B,D。然后结合已知条件排除C,得到A
,排除B,D。然后结合已知条件排除C,得到A
[考点定位]本试题考察了导数来解决函数单调性的运用。通过分析解析式的特点,考查了分析问题和解决问题的能力。
21.(2009天津卷文)设函数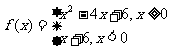 则不等式
则不等式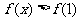 的解集是( )
的解集是( )
A.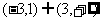 B.
B.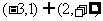
C. D.
D.
答案 A
解析 由已知,函数先增后减再增
当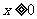 ,
,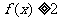
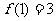 令
令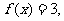
解得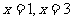 。
。
当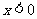 ,
,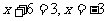
故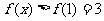 ,解得
,解得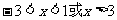
[考点定位]本试题考查分段函数的单调性问题的运用。以及一元二次不等式的求解。
20.(2009江西卷理)设函数 的定义域为
的定义域为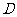 ,若所有点
,若所有点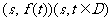 构成一个正方形区域,则
构成一个正方形区域,则 的值为 ( )
的值为 ( )
A. B.
B. C.
C. D.不能确定
D.不能确定
答案 B
解析 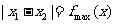 ,
,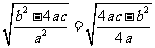 ,
,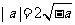 ,
,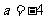 ,选B
,选B
19.(2009江西卷理)函数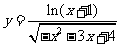 的定义域为 ( )
的定义域为 ( )
A.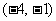 B.
B.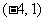 C.
C. D.
D.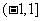
答案 C
解析 由 .故选C
.故选C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com