
5.在三棱柱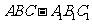 中,各棱长相等,侧掕垂直于底面,点
中,各棱长相等,侧掕垂直于底面,点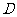 是侧面
是侧面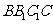 的中心,则
的中心,则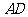 与平面
与平面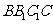 所成角的大小是 ( )
所成角的大小是 ( )
A.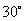 B.
B.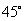 C.
C.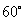 D.
D.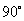
4. 如果函数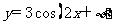 的图像关于点
的图像关于点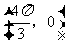 中心对称,那么
中心对称,那么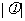 的最小值为(A)
的最小值为(A)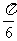 (B)
(B)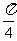 (C)
(C)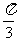 (D)
(D) 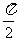
3. 设 、
、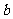 、
、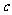 是单位向量,且
是单位向量,且 ·
·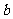 =0,则
=0,则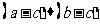 的最小值为 ( )
的最小值为 ( )
(A) (B)
(B)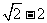 (C)
(C)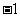 (D)
(D)
2.已知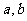 是实数,则“
是实数,则“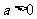 且
且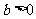 ”是“
”是“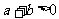 且
且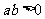 ”的 ( )
”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
1.设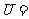
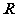 ,
,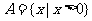 ,
,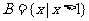 ,则
,则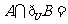 ( )
( )
A.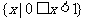 B.
B.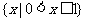 C.
C.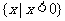 D.
D.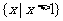
22.(本题满分14分)已知函数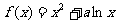 .
.
(Ⅰ)当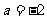 时,求函数
时,求函数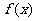 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若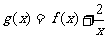 在
在 上是单调增函数,求实数a的取值范围.
上是单调增函数,求实数a的取值范围.
平邑县高考补习学校第四次阶段性考试
21. (本小题满分12分)已知直线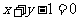 与椭圆
与椭圆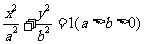 相交于
相交于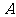 、
、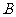 两点,
两点,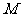 是线段
是线段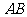 上的一点,
上的一点,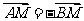 ,且点M在直线
,且点M在直线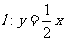 上
上
(1)求椭圆的离心率;
(2)若椭圆的焦点关于直线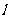 的对称点在单位圆
的对称点在单位圆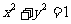 上,求椭圆的方程。
上,求椭圆的方程。
20.(本题满分12分)某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用12万元,以后每年都增加4万元,每年捕鱼收益50万元.
(Ⅰ)问第几年开始获利?
(Ⅱ)若干年后,有两种处理方案:①年平均获利最大时,以26万元出售该渔船;②总纯
收入获利最大时,以8万元出售该渔船. 问哪种方案最合算?
19. (本小题满分12分)如图,在直角梯形
(本小题满分12分)如图,在直角梯形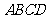 中,
中,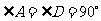 ,
,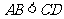 ,
, 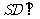 平面
平面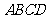 ,
,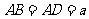 ,
,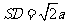 .
.
(Ⅰ)求证:平面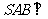 平面
平面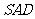 ;
;
(Ⅱ)设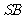 的中点为
的中点为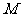 ,当
,当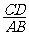 为何值时,能使
为何值时,能使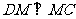 ? 请给出证明.
? 请给出证明.

18.(本小题满分12分) 已知数列{an}的各项均为正数,观察程序框图,若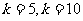 时,分别有
时,分别有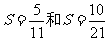 令
令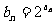 ,
,
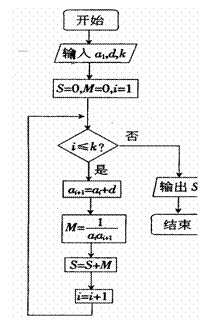 (I)求数列{an}的通项公式
(I)求数列{an}的通项公式
(II)令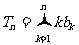 ,求
,求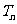
|
题 号 |
分 数 |
|
填 空 题 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
总 分 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com