
20.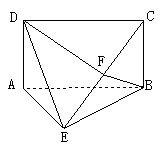 (本大题共15分)如图所示,ABCD为矩形,
(本大题共15分)如图所示,ABCD为矩形,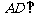 平面ABE,
平面ABE, ,F为CE上的点,且
,F为CE上的点,且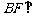 平面ACE.
平面ACE.
(1)求证: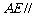 平面BFD;
平面BFD;
(2)求证: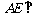 平面BCE;
平面BCE;
(3)求平面BDF与平面ABE所成的二面角的正弦值.
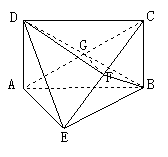 (1)证明:连AC交BD于G,由题意可得G是AC的中点,可得F是EC的中点.
(1)证明:连AC交BD于G,由题意可得G是AC的中点,可得F是EC的中点.
在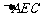 中,
中,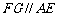 ,
,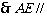 平面BFD. ………5分
平面BFD. ………5分
(2) 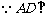 平面ABE,
平面ABE,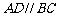 ,
,
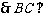 平面ABE,则
平面ABE,则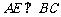 ,
,
又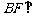 平面ACE,则
平面ACE,则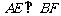 ,
,
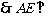 平面BCE. ……………………………………10分
平面BCE. ……………………………………10分
(3)可以以AB中点O为原点,OE为x轴,OB为y轴,
OG为z轴,建立空间直角坐标系.通过计算法向量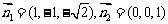 ,
,
计算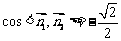 ,所以平面BDF与平面ABE所成的二面角的正弦值为
,所以平面BDF与平面ABE所成的二面角的正弦值为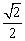 .
.
…………………………………………………………………………………………………15分
19.(本大题共14分)一种电脑屏幕保护画面,只有符号“O”和“ ”随机地反复出现,每秒钟变化一次,每次变化只出现“O”和“
”随机地反复出现,每秒钟变化一次,每次变化只出现“O”和“ ”之一,其中出现“O”的概率为
”之一,其中出现“O”的概率为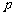 ,出现“
,出现“ ”的概率为
”的概率为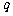 ,若第
,若第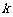 次出现“O”,则记
次出现“O”,则记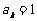 ;出现“
;出现“ ”,则记
”,则记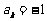 .令
.令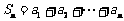 .
.
(1)当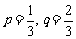 时,求
时,求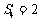 的概率;
的概率;
(2)当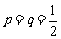 时,记
时,记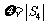 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
解:(1)因为 ,即出现“O”的次数是3次,出现“
,即出现“O”的次数是3次,出现“ ”的次数是1次,
”的次数是1次,
所以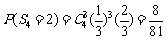 .………………………………………………………………5分
.………………………………………………………………5分
(2)对于 的可能取值有
的可能取值有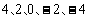 ,因此
,因此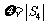 的可能取值为
的可能取值为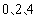 ,
,
又 ,
,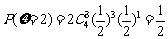 ,
,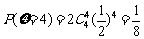 ,
,
所以 的分布列为
的分布列为
 |
0 |
2 |
4 |
|
P |
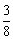 |
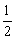 |
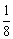 |
……………………………………………………………………………………………………10分
所以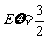 .……………………………………………………………………………………14分
.……………………………………………………………………………………14分
18.(本大题共14分)已知函数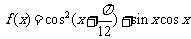 .
.
(1)求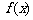 的最小正周期和图象的对称中心;
的最小正周期和图象的对称中心;
(2)若存在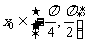 使得不等式
使得不等式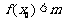 成立,求
成立,求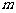 的取值范围.
的取值范围.
解:化简得: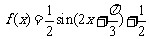 …………………………………………………………6分
…………………………………………………………6分
(1) 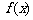 的最小正周期为
的最小正周期为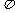 ,……………………………………………………………………7分
,……………………………………………………………………7分
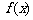 的对称中心
的对称中心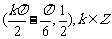 ;…………………………………………………………9分
;…………………………………………………………9分
(2) 由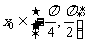
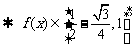 ,…………………………………………………12分
,…………………………………………………12分
存在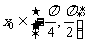 使得不等式
使得不等式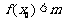 成立,得
成立,得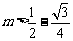 .……………………………14分
.……………………………14分
17.给出下列四个命题:①函数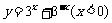 的最小值为2;②在数列
的最小值为2;②在数列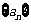 中,
中, ,
,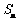 是其前
是其前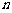 项和,且满足
项和,且满足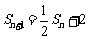 ,则数列
,则数列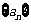 是等比数列;③若
是等比数列;③若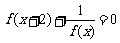 ,则函数
,则函数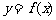 是以4为周期的周期函数;④若函数
是以4为周期的周期函数;④若函数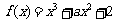 的图象关于点
的图象关于点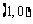 对称,则
对称,则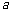 的值为
的值为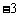 .则正确命题的序号是 ▲ . ③④
.则正确命题的序号是 ▲ . ③④
16.已知函数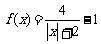 的定义域为
的定义域为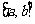 (
(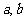 为整数),值域为
为整数),值域为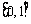 ,则满足条件的整数对
,则满足条件的整数对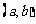 共有 ▲ 个.5
共有 ▲ 个.5
15.从6种不同的作物种子中选出4种放入4个不同的瓶子中展出,如果甲、乙两种种子不能放入第1号瓶内,且丙、丁不能同时入选,那么不同的放法共有 ▲ 种.132
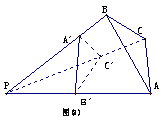
14.由图(1)有面积关系: 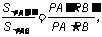 则由(2) 有体积关系:
则由(2) 有体积关系: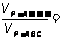 ▲ .
▲ . 
13.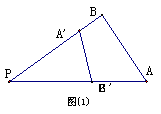
 若
若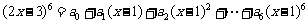 ,则
,则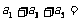 ▲ .
▲ .
12.在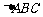 中,边长
中,边长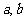 是方程
是方程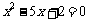 的两个根,
的两个根,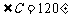 ,则边长
,则边长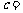 ▲ .
▲ .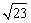
11.若复数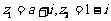 ,且
,且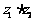 为纯虚数,则实数
为纯虚数,则实数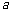 等于 ▲ .
等于 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com