21、(12分)已知定义域为R的二次函数f(x)的最小值为0，且有f(1+x)＝f(1－x), 直线g(x)＝4(x－1)的图象被f(x)的图象截得的弦长为4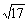，数列{a_n}满足a₁＝2,

(a_n+1－a_n)g(a_n)+f(a_n)＝0 (n∈N*).

(1)求函数f(x)的解析式；

(2)求数列{a_n}的通项公式；

(3)设b_n＝3f(a_n)－g(a_n+1)，求数列{b_n}的最值及相应的n值。

20、(12分)已知函数f(x)＝x³―ax―1.

(1)若f(x)在实数集R上单调递增，求实数a的取值范围；

(2)是否存在实数a，使f(x)在(－1, 1)上单调递减？若存在，求出a的取值范围，若不存在，说明理由。

19、(12分)已知斜三棱柱ABC-A₁B₁C₁，侧面ACC₁A₁与底面ABC垂直，

∠ABC＝90°，BC＝2，AC＝2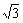，且AA₁⊥A₁C，AA₁＝A₁C.

(1)试判断AA₁与平面A₁BC是否垂直，并说明理由；

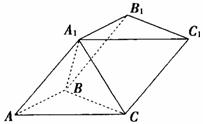(2)求侧面BB₁C₁C与底面ABC所成锐二面角的余弦值。

18、(12分)某工厂每月生产某种产品三件，经检测发现，工厂生产该产品的合格率为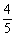，已知生产一件合格品能盈利25万元，生产一件次品将会亏损10万元，假设该产品任何两件之间合格与否相互没有影响。

(1)求工厂每月盈利额ξ(万元)的所有可能取值；

(2)若该工厂制定了每月盈利额不低于40万元的目标，求该工厂达到盈利目标的概率。

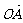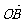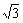17、(12分)已知x∈R, 向量＝(acos²x, 1), ＝(2, asin2x－a), f(x)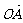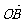＝·, a≠0.

(1)求函数f(x)的解析式，并求当a＞0时，f(x)的单调增区间；

(2)当x∈[0, 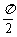]时，f(x)的最大值为5，求a的值。

16、在△ABC中，AB＝3，AC＝5，若O为△ABC的外心，则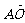·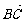的值为　　　　　　　 。

15、若函数f(x)＝ax³+x+1有极值，则实数a的取值范围为　　　　　　 　 。

14、过椭圆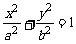的左焦点F且倾斜角为60°的直线交椭圆于A、B两点，若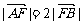，则椭圆的离心率e＝ 　　　　 。

13、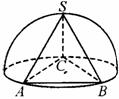如图，已知各顶点都在半球面上的正三棱锥S-ABC。若AB＝a，则该三棱锥的体积为　　　　　 。

12、已知数列{a_n}满足a_n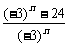＝(n∈N*)，其前n项和为S_n，则满足不等式|S_n―n―6|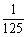＜的最小整数n是(　)

　　 A．5　　　　　　 B．6　　　　　　 C．7　　　　　　 D．8