
1.下列关于真核细胞结构和功能叙述中,错误的是 ( )
A. 抑制线粒体的功能会影响主动运输
B. 核糖体由RNA和蛋白质构成
C. 有分泌功能的细胞才有高尔基体
D. 溶酶体可消化细胞器碎片
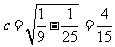 ,椭圆的离心率
,椭圆的离心率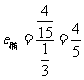 .
.
∵椭圆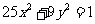 的焦点在
的焦点在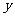 轴上,且与双曲线有公共焦点,
轴上,且与双曲线有公共焦点,
因此设双曲线的方程为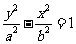 ,
,
且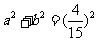 , ①
, ①
∵椭圆与双曲线的离心率之和为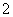 ,
,
而双曲线的离心率为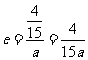 ,
,
∴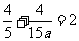 ,②
,②
由①②解得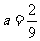 ,
,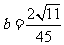
∴所求双曲线方程为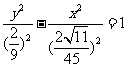 .
.
作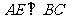 于
于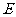 ,连接
,连接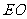 .
.
则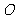 、
、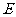 分别为
分别为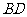 、
、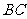 的中点,∴
的中点,∴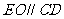 .
.
∵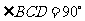 ,∴
,∴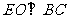 ,
,
而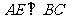 ,所以
,所以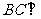 面
面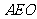 ,
,
∴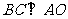 ,又
,又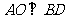 ,
,
∴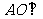 面
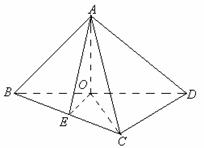
面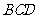 .
.
 连接
连接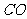 ,则
,则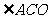 为
为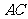 与面
与面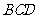 所成的角.
所成的角.
∵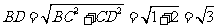 ,
,
∴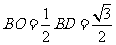 ,
,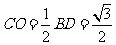 ,
,
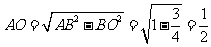 .
.
在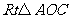 中,
中,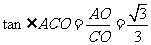 ,
,
∴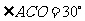 ,即
,即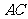 与平面
与平面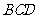 所成的角为
所成的角为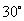 .
.
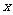 |
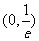 |
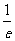 |
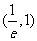 |
 |
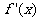 |
+ |
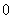 |
- |
- |
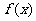 |
单调增 |
极大值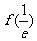 |
单调减 |
单调减 |
(Ⅱ)在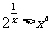 两边取对数,得
两边取对数,得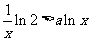 ,由于
,由于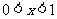 ,
,
所以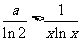 .
.
由(Ⅰ)的结果可知,当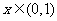 时,
时,
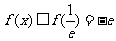 ,要使①式对所有
,要使①式对所有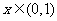 成立,
成立,
当且仅当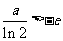 ,即
,即 .
.
(Ⅰ)求函数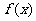 的单调区间;
的单调区间;
(Ⅱ)已知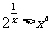 对任意
对任意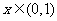 成立,求实数
成立,求实数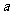 的取值范围.
的取值范围.
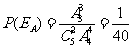 ,即甲、乙两人同时分到
,即甲、乙两人同时分到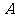 岗位的概率是
岗位的概率是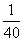 .
.
(Ⅱ)记甲、乙两人同时分到同一岗位为事件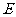 ,
,
那么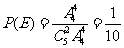 ,
,
所以,甲、乙两人不在同一个岗位的概率是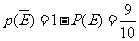 .
.
(Ⅲ)随机变量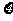 可能取的值为
可能取的值为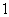 ,
,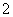 .
.
则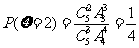 ,
,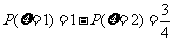 .
.
所以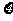 的分布列是
的分布列是
|
ξ |
1 |
2 |
|
P |
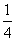 |
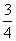 |
至少有一名战士.
(Ⅰ)求甲、乙两人同时分到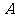 岗位的概率;
岗位的概率;
(Ⅱ)求甲、乙两人不在同一个岗位的概率;
(Ⅲ)设随机变量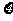 为这五名战士中分到
为这五名战士中分到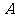 岗位的人数,求
岗位的人数,求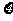 的分布列.
的分布列.
两式相减得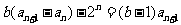 ,即
,即 , ①
, ①
(Ⅰ)当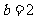 时,由①知
时,由①知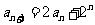 ,
,
于是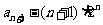
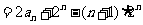
 ,
,
又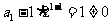 ,所以
,所以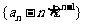 是首项为
是首项为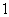 ,公比为
,公比为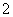 的等比数列.
的等比数列.
(Ⅱ)当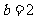 时,由(Ⅰ)知
时,由(Ⅰ)知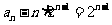 ,即
,即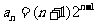 ;
;
当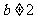 时,由①得
时,由①得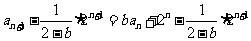
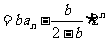
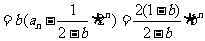 ,
,
故有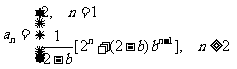 .
.
(Ⅰ)证明:当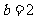 时,
时,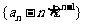 是等比数列;
是等比数列;
(Ⅱ)求 的通项公式.
的通项公式.
3.解:设圆心为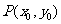 ,由
,由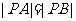 ,
,
得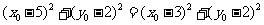 , ①
, ①
又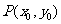 在直线
在直线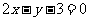 上,则
上,则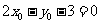 ,②
,②
由①②解得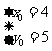 ,即所求圆的圆心为
,即所求圆的圆心为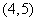 ,半径为
,半径为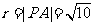 .
.
故所求圆方程为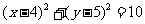 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com