
3.⑥→⑤→④城市一月均温的变化体现了 ( )
A.从赤道向两极的地域分异规律 B.从沿海向内陆的地域分异规律
C.山地垂直地域分异规律 D.非地带性
2.温哥华西侧洋流对该地环境的影响是 ( )
A.增温减湿 B.减温减湿 C.增温增湿 D.减温增湿
表1中序号①至⑥为我国六个省会城市。回答3-6题。
表1 (单位:℃)
|
序号 |
一月均温 |
七月均温 |
年均温 |
序号 |
一月均温 |
七月均温 |
年均温 |
|
① |
-0.3 |
27.3 |
14.2 |
④ |
-2.9 |
26.6 |
12.7 |
|
② |
4.7 |
29.3 |
17.2 |
⑤ |
2.1 |
82.3 |
15.7 |
|
③ |
13.3 |
28.4 |
21.8 |
⑥ |
15.8 |
28.8 |
22.9 |
1.在当地时间2月14日16时30分开始进行的双人混合花样滑冰的比赛中,中国三对选手 表现出色。北京电视台开始现场转播此次比赛的时间是 ( )
A.14日18时30分 B.15日0时30分
C.14日23时30分 D.15日8时30分
2010.4
第I卷(单项选择题)
本卷共35小题,每小题4分,共140分。在每小题列出的四个选项中,只有一项是最符合题目要求的。
2010年冬季奥运会于2月12日至28日在加拿大的温哥华(西八区)举行。回答1、2题。
(15)(本小题共12分)
在 中,角
中,角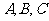 所对的边分别为
所对的边分别为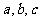 ,满足
,满足 ,且
,且 的面积为
的面积为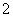 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,求
,求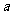 的值.
的值.
(16)(本小题共13分)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了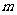 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为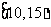 ,
, ,
, ,
,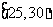 ,
, ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求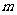 ;
;
 (Ⅱ)工厂规定从各组中任选1人进行再培训,则选取5人的概率是多少?
(Ⅱ)工厂规定从各组中任选1人进行再培训,则选取5人的概率是多少?
(17)(本小题共14分)
 三棱柱
三棱柱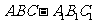 中,侧棱与底面垂直,
中,侧棱与底面垂直,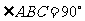 ,
, ,
, 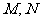 分别是
分别是 ,
,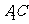 的中点.
的中点.
(Ⅰ)求证: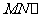 平面
平面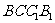 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角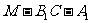 的余弦值.
的余弦值.
(18)(本小题共14分)
已知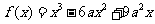 (
( ).
).
(Ⅰ)求函数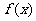 的单调递减区间;
的单调递减区间;
(Ⅱ)当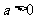 时,若对
时,若对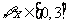 有
有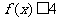 恒成立,求实数
恒成立,求实数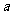 的取值范围.
的取值范围.
(19)(本小题共14分)
已知抛物线 ,点
,点 关于
关于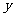 轴的对称点为
轴的对称点为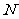 ,直线
,直线 过点
过点 交抛物线于
交抛物线于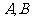 两点.
两点.
(Ⅰ)证明:直线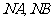 的斜率互为相反数;
的斜率互为相反数;
(Ⅱ)求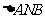 面积的最小值;
面积的最小值;
(Ⅲ)当点 的坐标为
的坐标为 ,且
,且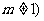 .根据(Ⅰ)(Ⅱ)推测并回答下列问题(不必说明理由):
.根据(Ⅰ)(Ⅱ)推测并回答下列问题(不必说明理由):
① 直线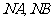 的斜率是否互为相反数?
的斜率是否互为相反数?
② 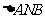 面积的最小值是多少?
面积的最小值是多少?
(20)(本小题共13分)
已知数列
 中,
中,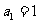 ,
, 且
且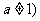 ,其前
,其前 项和为
项和为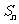 ,且当
,且当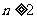 时,
时,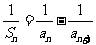 .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)若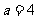 ,令
,令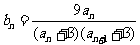 ,记数列
,记数列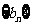 的前
的前 项和为
项和为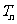 .设
.设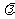
 是整数,问是否存在正整数
是整数,问是否存在正整数 ,使等式
,使等式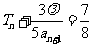 成立?若存在,求出
成立?若存在,求出 和相应的
和相应的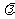 值;若不存在,请说明理由.
值;若不存在,请说明理由.
(考生务必将答案答在答题卡上,在试卷上作答无效)
崇文区2009-2010学年度第二学期统一练习(一)
(9)如果复数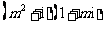 (其中
(其中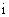 是虚数单位)是实数,则实数
是虚数单位)是实数,则实数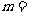
 ___________.
___________.
(10)若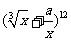 的展开式中的常数项为
的展开式中的常数项为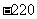 ,则实数
,则实数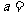
 ___________.
___________.
(11)将参数方程 (
( 为参数)化成普通
为参数)化成普通 方程为 .
方程为 .
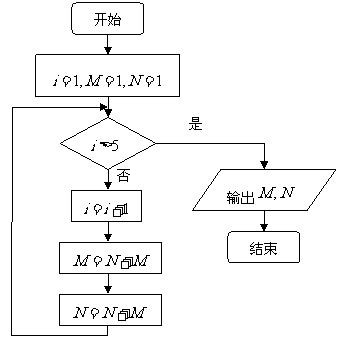
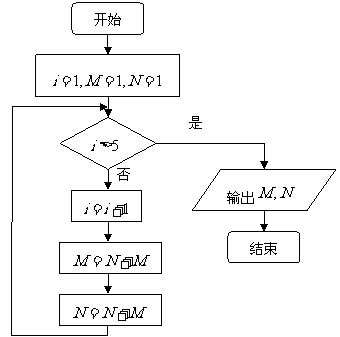 (12)某程序框图如图所示,该程序运行后输出
(12)某程序框图如图所示,该程序运行后输出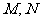 的值分别为
.
的值分别为
.
(13)若数列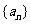 的前
的前 项和为
项和为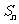 ,则
,则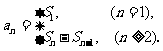
若数列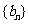 的前
的前 项积为
项积为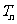 ,类
,类 比
比 上述结果,则
上述结果,则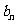 =_________;
=_________;
此时,若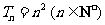 ,则
,则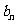 =___________.
=___________.
(14)定义在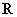 上的函数满足
上的函数满足 ,
,
且当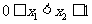 时,
时,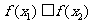 ,则
,则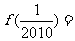 _________________.
_________________.
(1)已知全集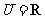 ,集合
,集合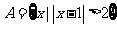 ,
,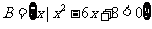 ,则集合
,则集合
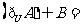
(A)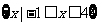 (B)
(B)
(C)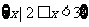 (D)
(D) 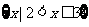
(2)一个单位共有职工200人,其中不超过45岁的有120人,超过45岁的有80人. 为了调查职工的健康状况,用分层抽样的方法从全体职工中抽出一个容量为25的样本,应抽取不超过45岁的职工人数为
 (A)
5
(B) 10 (C)15 (D)50
(A)
5
(B) 10 (C)15 (D)50
(3)已知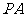 是
是
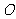 的切线,切点为
的切线,切点为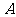 ,
, ,
,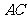 是
是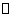
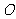
的直径, 交
交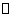
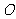 于点
于点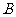 ,
,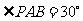 ,则
,则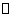
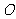 的
的
半径为
(A)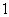 (B)
(B)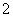
(C)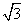 (D)
(D)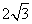
(4)已知等比数列 为递增数列,且
为递增数列,且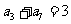 ,
,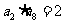 ,则
,则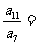
(A)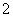 (B)
(B)
 (C)
(C) 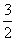 (D)
(D)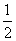
(5)已知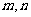 是两条不同直线,
是两条不同直线,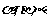 是三个不同平面,下列命题中正确的为
是三个不同平面,下列命题中正确的为
(A)若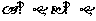 则
则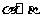 (B)若
(B)若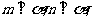 则
则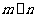
(C)若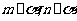 ,则
,则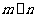 (D)若
(D)若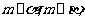 则
则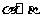
(6)设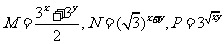 (其中
(其中
 ), 则
), 则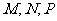 大小关系为
大小关系为
(A)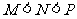 (B)
(B)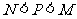 (C)
(C)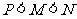 (D)
(D)
(7)2位男生和3位女生共5位同学站成一排.若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数为
(A)36
(B)4 2
(C) 48
(D)
60
2
(C) 48
(D)
60
(8)设定义在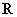 上的函数
上的函数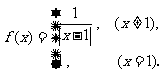 若关于
若关于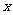 的方程
的方程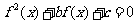 有3个不同的实数解
有3个不同的实数解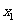 ,
,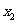 ,
,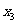 ,则
,则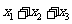 等于
等于
(A) 3 (B)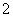 (C)
(C)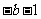 (D)
(D)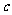
崇文区2009-2010学年度第二学期统一练习(一)
高三数学(理科) 2010.4
第Ⅱ卷(共110分)
(9)若 ,则
,则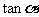 =
.
=
.
(10)如果复数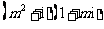 (其中
(其中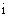 是虚数单位)是实数,则实数
是虚数单位)是实数,则实数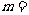

 ___________.
___________.
 (11)从
(11)从 张扑克牌(没有大小王)中随机的抽一张牌,这张牌是
张扑克牌(没有大小王)中随机的抽一张牌,这张牌是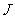 或
或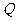 或
或 的概率为_______.
的概率为_______.
(12)某程序框图如图所示,该程序运行后
输出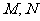 的值分别为 .
的值分别为 .
(13)若数列 的前
的前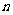 项和为
项和为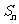 ,则
,则
若数列 的前
的前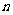 项积为
项积为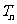 ,类比上述结果,则
,类比上述结果,则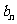 =_________;
=_________;
此时,若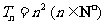 ,则
,则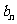 =___________.
=___________.
(14)关于平面向量有下列四个命题:
①若 ,则
,则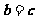 ; ②已知
; ②已知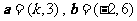 .若
.若 ,则
,则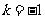 ;
;
③非零向量 和
和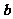 ,满足
,满足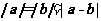 ,则
,则 与
与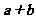 的夹角为
的夹角为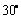 ;
;
④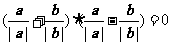 .
.
其中正确的命题为___________.(写出所有正确命题的序号) 三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.
(15)(本小题共12分)
在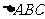 中,角
中,角 所对的边分别为
所对的边分别为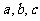 ,满足
,满足 ,且
,且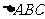 的面积为
的面积为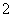 .
.
(Ⅰ)求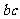 的值;
的值;
(Ⅱ)若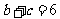 ,求
,求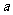 的值.
的值.
(16)(本小题共13分)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为 ,
, ,
, ,
,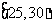 ,
,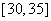 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工
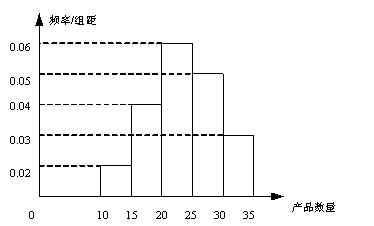 人不在同一组的概率是多少?
人不在同一组的概率是多少?
(17)(本小题共14分)
 三棱柱
三棱柱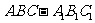 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,
, 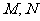 分别是
分别是 ,
, 的中点.
的中点.
(Ⅰ)求证: 平面
平面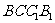 ;
;
(Ⅱ)求证: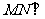 平面
平面 ;
;
(Ⅲ)求三棱锥
 的体积.
的体积.
(18)(本小题共14分)
已知函数 (
( ).
).
(Ⅰ)求函数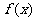 的单调递减区间;
的单调递减区间;
(Ⅱ)当 时,若对
时,若对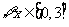 有
有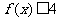 恒成立,求实数
恒成立,求实数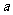 的取值范围.
的取值范围.
(19)(本小题共14分)
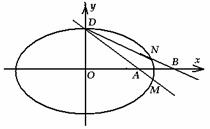 已知椭圆
已知椭圆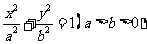 短轴
短轴 的一个端点
的一个端点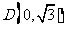 ,离心率
,离心率 .过
.过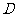 作直线
作直线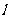 与椭圆交于另一点
与椭圆交于另一点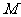 ,与
,与 轴交于点
轴交于点 (不同于原点
(不同于原点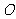 ),点
),点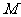 关于
关于 轴的对称点为
轴的对称点为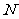 ,直线
,直线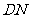 交
交 轴于点
轴于点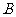 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)求  的值.
的值.
(20)(本小题共13分)
已知数列 的前
的前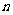 项和为
项和为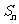 ,且
,且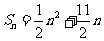 .
.
数列 满足
满足 (
( ),且
),且 ,
,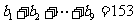 .
.
(Ⅰ)求数列 ,
,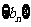 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列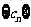 的前
的前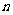 项和为
项和为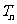 ,求使不等式
,求使不等式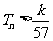 对一切
对一切 都成立的最大正整数
都成立的最大正整数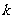 的值;
的值;
(Ⅲ)设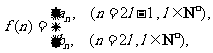 是否存在
是否存在 ,使得
,使得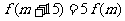 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明
的值;若不存在,请说明 理由.
理由.
(考生务必将答案答在答题卡上,在试卷上作答无效)
崇文区2009-2010学年度第二学期统一练习(一)
(1)已 知全集
知全集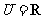 ,集合
,集合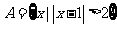 ,
, ,则集合
,则集合
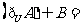
(A)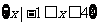 (B)
(B)
(C)  (D)
(D)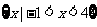
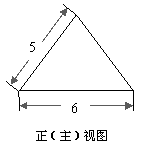
(2)已知幂函数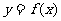 的图象过(4,2)点,则
的图象过(4,2)点,则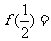
 (A)
(A)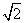 (B)
(B) (C)
(C)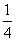 (D)
(D)
 (3)有一个几何体的三视图及其尺寸如图
(3)有一个几何体的三视图及其尺寸如图
(单位: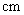 ),该几何体的表面积和体积为
),该几何体的表面积和体积为
(A)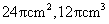
(B)
 (C)
(C)
(D)以上都不正确
 (4)若直线
(4)若直线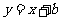 与圆
与圆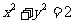 相切,则
相切,则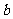 的值为
的值为
(A)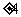 (B)
(B) (C)
(C) (D)
(D)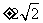
(5)将函数 的图象向右平移
的图象向右平移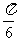 个单位后,其图象的一条对称轴方程为
个单位后,其图象的一条对称轴方程为
(A) 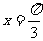 (B)
(B) 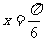 (C)
(C)  (D)
(D) 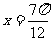
(6)已知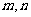 是两条不同直线,
是两条不同直线,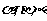 是三个不同平面,下列命题中正确的为
是三个不同平面,下列命题中正确的为
(A)若 则
则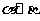 (B)若
(B)若 则
则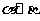
(C)若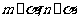 ,则
,则 (D)若
(D)若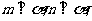 则
则
(7)若 ,函数
,函数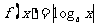 ,
,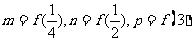 ,则
,则
(A)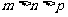 (B)
(B) (C)
(C)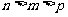 (D)
(D)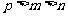
(8)如果对于任 意实数
意实数 ,
, 表示不超过
表示不超过 的最大整数. 例如
的最大整数. 例如 ,
,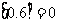 .
.
那么“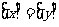 ”是“
”是“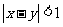 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
崇文区2009-2010学年度第二学期统一练习(一)
高三数学(文科) 2010.4
第Ⅱ卷(共110分)
第二节:书面表达(25分)
请你根据下面一幅图和一首诗,写一篇说明“书的作用”的短文。
注意:可根据小诗的提示适当增加必要的细节,使内容和意思衔接。(字数为100左右)
层层宝库找开来,黑宝纵横一排排。
能记诸般悠悠事,不分古今和中外。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com