
20.(本小题满分13分)
已知首项不为零的数列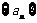 的前
的前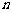 项和为
项和为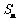 ,若对任意的
,若对任意的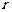 ,
,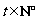 ,都有
,都有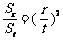 .
.
(Ⅰ)判断数列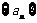 是否为等差数列,并证明你的结论;
是否为等差数列,并证明你的结论;
(Ⅱ)若数列 的第
的第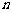 项
项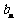 是数列
是数列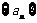 的第
的第 项
项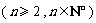 ,且
,且 ,
, ,求数列
,求数列 的前
的前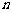 项和
项和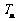 .
.
19.(本小题满分13分)
在一条笔直的工艺流水线上有 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为 ,
,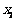 ,
,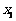 ,每个工作台上有若干名工人.现要在
,每个工作台上有若干名工人.现要在 与
与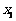 之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
(Ⅰ)若每个工作台上只有一名工人,试确定供应站的位置;
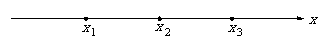 (Ⅱ)设工作台从左到右的人数依次为
(Ⅱ)设工作台从左到右的人数依次为 ,
, ,
, ,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
|
18.(本小题满分12分)
 如图
如图 ,
, 是圆
是圆 的的直径,点
的的直径,点 是弧
是弧 的中点,
的中点, ,
, 分别是
分别是 ,
, 的中点,
的中点,
平面 .
.
(Ⅰ)求异面直线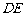 与
与 所成的角;
所成的角;
(Ⅱ)证明  平面
平面 .
.
|
17.(本小题满分12分)
甲,乙两人进行射击比赛,每人射击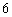 次,他们命中的环数如下表:
次,他们命中的环数如下表:
|
甲 |
5 |
8 |
7 |
9 |
10 |
6 |
|
乙 |
6 |
7 |
4 |
10 |
9 |
9 |
(Ⅰ)根据上表中的数据,判断甲,乙两人谁发挥较稳定;
(Ⅱ)把甲6次射击命中的环数看成一个总体,用简单随机抽样方法从中抽取两次命中的环数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过 的概率.
的概率.
16.(本小题满分12分)
在 中,角
中,角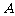 ,
,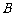 ,
, 所对的边分别为
所对的边分别为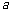 ,
, ,
,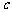 ,向量
,向量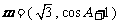 ,
,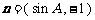 ,且
,且 .
.
(Ⅰ)求角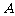 的大小;
的大小;
(Ⅱ)若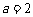 ,
, ,求
,求 的值.
的值.
15.定义运算符号“ ”:表示若干个数相乘,例如:
”:表示若干个数相乘,例如: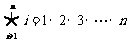 .记
.记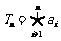 ,
,
其中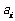 为数列
为数列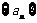 中的第
中的第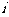 项.
项.
(1)若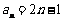 ,则
,则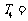 ;
;
(2)若 ,则
,则 .
.
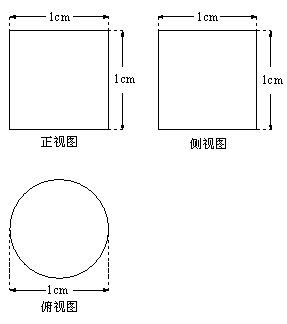
14.一空间几何体的三视图(单位: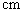 )如图
)如图 所示,则此几何体的表面积是
所示,则此几何体的表面积是 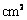 .
.


|
13.某人午觉醒来,发现表停了,他打开收音机,想听电台的整点报时,则他等待的时间不多于5分钟的概率为 .
12.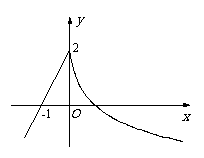 如图
如图 ,函数
,函数 的图象是
的图象是
一条连续不断的曲线,则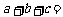 .
.
|
11. 某化工厂准备对一化工产品进行技术改造,决定优选加工温度,假定最佳温度在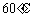 到
到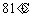 之间.现用分数法进行优选,则第二次试点的温度为
之间.现用分数法进行优选,则第二次试点的温度为 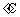 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com