
4.观察下面一幅漫画,根据要求完成题目。(5分)

(1)写一段话描绘画面内容,要求至少运用一种修辞格。
(3分)
答: ▲ ▲
(2)用一句话点明漫画内涵,不超过15字。(2分)
答: ▲ ▲
2.下列各旬中,加点成语使用恰当的一项是(3分)
A.“六·三○”特大醉酒驾车肇事案司机张明宝一审被判无期徒刑,这一判罚引起广泛争议,许多人认为张明宝致五死四伤,后果特别严重,罚不当罪,判处死刑也不为过。
B.随着新年钟声的敲响,围坐在广场音乐水池旁的人们骤然爆发出一阵由衷的欢呼,他们情不自禁的手拉着手,忘乎所以地唱着、跳着。
C.本书自问世以来印数超过500万册,作为传统实用的基本英语语法书,能在众多同类出版物中脱颖而出,关键在于它有极强的针对性。
D.杜郎口中学三面黑板学生争相去写、去画的真实课堂把他们“学生是学习的主人,是具有独立人格的平等的人”的理念演绎得淋漓尽致。
1.下列词语中加点的字,每对读音都不相同的一组是(3分)
A.纰缪/未雨绸缪 哥俩/肮脏伎俩 称职/称体裁衣
B.躯壳/金蝉脱壳 艾草/自怨自艾 扁担/一叶扁舟
C.诏书/昭然若揭 对峙/恃才傲物 桀骜/估屈聱牙
D.锋镝/嫡系后裔 倾轧/安营扎寨 裨将/稗官野史
7.数列求和的常用方法:
(1)公式法:
①等比数列 的前
的前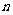 项和Sn=2n-1,则
项和Sn=2n-1,则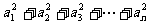 =_____(答:
=_____(答: );
);
②计算机是将信息转换成二进制数进行处理的。二进制即“逢2进1”,如 表示二进制数,将它转换成十进制形式是
表示二进制数,将它转换成十进制形式是 ,那么将二进制
,那么将二进制 转换成十进制数是_______(答:
转换成十进制数是_______(答: )
)
(2)分组求和法:
(08天津文20)在数列 中,
中, ,
, ,
, .
.
(Ⅰ)证明数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的前
的前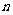 项和
项和 ;
;
(Ⅰ)证明:由题设 ,得
,得
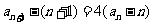 ,
, .
.
又 ,所以数列
,所以数列 是首项为
是首项为 ,且公比为
,且公比为 的等比数列.
的等比数列.
(Ⅱ)解:由(Ⅰ)可知 ,于是数列
,于是数列 的通项公式为
的通项公式为
 .
.
所以数列 的前
的前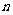 项和
项和 .
.
(3)倒序相加法:
①求证: ;
;
②已知 ,则
,则 =______(答:
=______(答: )
)
(4)错位相减法:
(1)设 为等比数列,
为等比数列, ,已知
,已知 ,
, ,①求数列
,①求数列 的首项和公比;②求数列
的首项和公比;②求数列 的通项公式.(答:①
的通项公式.(答:① ,
, ;②
;② );
);
(2) (2009山东卷文)等比数列{ }的前n项和为
}的前n项和为 , 已知对任意的
, 已知对任意的 ,点
,点 ,均在函数
,均在函数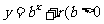 且
且 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(11)当b=2时,记  求数列
求数列 的前
的前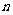 项和
项和
解:因为对任意的 ,点
,点 ,均在函数
,均在函数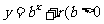 且
且 均为常数)的图像上.所以得
均为常数)的图像上.所以得 ,
,
当 时,
时, ,
,
当 时,
时,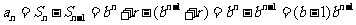 ,
,
又因为{ }为等比数列, 所以
}为等比数列, 所以 , 公比为
, 公比为 , 所以
, 所以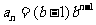
(2)当b=2时, ,
, 
则
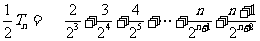
相减,得


所以
[命题立意]:本题主要考查了等比数列的定义,通项公式,以及已知 求
求 的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前
的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前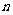 项和
项和 .
.
(3)设 ,
, ,求数列
,求数列 的前
的前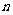 项和
项和 .
.
 ,
,


 ,
,

(5)裂项相消法:
(1)求和: (答:
(答: );
);
(2)在数列 中,
中, ,且Sn=9,则n=_____(答:99);
,且Sn=9,则n=_____(答:99);
(6)通项转换法:求和: (答:
(答: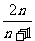 )
)
6.数列的通项的求法:
(1)构造法(2009四川卷理)设数列 的前
的前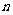 项和为
项和为 ,对任意的正整数
,对任意的正整数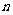 ,都有
,都有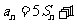 成立,记
成立,记 。求数列
。求数列 的通项公式。
的通项公式。
解:当 时,
时,
又 
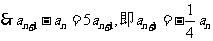
 数列
数列 成等比数列,其首项
成等比数列,其首项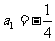 ,公比是
,公比是

 ……………………………………..3分
……………………………………..3分
(2)迭加法:(2009全国卷Ⅰ理)在数列 中,
中, 设
设 ,求数列
,求数列 的通项公式
的通项公式
解:由已知有
 利用累差迭加即可求出数列
利用累差迭加即可求出数列 的通项公式:
的通项公式:  (
( )
)
已知数列 满足
满足 ,
,
 ,则
,则 =________(答:
=________(答: )
)
①
已知 ,求
,求 (答:
(答: );
);
②
已知 ,求
,求 (答:
(答: );
);
③已知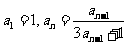 ,求
,求 (答:
(答: );
);
④已知数列满足 =1,
=1, ,求
,求 (答:
(答: )
)
⑤已知 的前
的前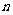 项和满足
项和满足 ,求
,求 (答:
(答: );
);
⑥数列 满足
满足 ,求
,求 (答:
(答: )
)
⑦已知数列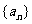 中,
中, ,前
,前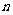 项和
项和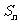 ,若
,若 ,求
,求 (答:
(答: )
)
⑧(全国2理21)设数列 的首项
的首项 .求
.求 的通项公式;
的通项公式;
解:由 整理得
整理得  .
.
又 ,所以
,所以 是首项为
是首项为 ,公比为
,公比为 的等比数列,得
的等比数列,得

设数列 满足
满足 ,
, .求数列
.求数列 的通项;
的通项;
(I)



验证 时也满足上式,
时也满足上式,
⑨(北京理10)若数列 的前
的前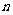 项和
项和 ,则此数列的通项公式为 ;数列
,则此数列的通项公式为 ;数列 中数值最小的项是第 项.
中数值最小的项是第 项.
解析:数列 的前
的前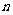 项和
项和 ,数列为等差数列,数列的通项公式为
,数列为等差数列,数列的通项公式为 =
= ,数列
,数列 的通项公式为
的通项公式为 ,其中数值最小的项应是最靠近对称轴
,其中数值最小的项应是最靠近对称轴 的项,即n=3,第3项是数列
的项,即n=3,第3项是数列 中数值最小的项。
中数值最小的项。
5.等比数列的性质:
(1)(2009辽宁卷理)设等比数列{  }的前n 项和为
}的前n 项和为 ,若
,若
 =3
,则
=3
,则  =
=
(A) 2 (B)
 (C)
(C)
 (D)3
(D)3
[解析]设公比为q ,则 =1+q3=3 Þ
q3=2
=1+q3=3 Þ
q3=2
于是 .
.
[答案]B
(2)各项均为正数的等比数列 中,若
中,若 ,则
,则 (答:10)。
(答:10)。
(3)已知 且
且 ,设数列
,设数列 满足
满足
 ,且
,且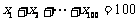 ,则
,则 . (答:
. (答: );
);
(4)(2009辽宁卷理)设等比数列{  }的前n 项和为
}的前n 项和为 ,若
,若
 =3
,则
=3
,则  =
=
(A) 2 (B)
 (C)
(C)
 (D)3
(D)3
[解析]设公比为q ,则 =1+q3=3 Þ
q3=2
=1+q3=3 Þ
q3=2
于是 .
.
[答案]B
(5)(2009宁夏海南卷理)等比数列 的前n项和为
的前n项和为 ,且4
,且4 ,2
,2 ,
, 成等差数列。若
成等差数列。若 =1,则
=1,则 =
=
(A)7 (B)8 (3)15 (4)16
解析: 4
4 ,2
,2 ,
, 成等差数列,
成等差数列, ,选C.
,选C.
(6)若 是等比数列,且
是等比数列,且 ,则
,则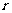 = (答:-1)
= (答:-1)
(7)设等比数列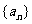 的公比为
的公比为 ,前
,前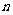 项和为
项和为 ,若
,若 成等差数列,则
成等差数列,则 的值为_____(答:-2)
的值为_____(答:-2)
(8)设数列 的前
的前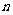 项和为
项和为 (
( ), 关于数列
), 关于数列 有下列三个命题:①若
有下列三个命题:①若 ,则
,则 既是等差数列又是等比数列;②若
既是等差数列又是等比数列;②若 ,则
,则 是等差数列;③若
是等差数列;③若 ,则
,则 是等比数列。这些命题中,真命题的序号是
(答:②③)
是等比数列。这些命题中,真命题的序号是
(答:②③)
4.等比数列的有关概念:
(1)等比数列的判断方法:
①(2009湖北卷文)设 记不超过
记不超过 的最大整数为[
的最大整数为[ ],令{
],令{ }=
}= -[
-[ ],则
],则 {
{ },[
},[ ],
],
A.是等差数列但不是等比数列 B.是等比数列但不是等差数列
C.既是等差数列又是等比数列 D.既不是等差数列也不是等比数列
[答案]B
[解析]可分别求得 ,
, .则等比数列性质易得三者构成等比数列.
.则等比数列性质易得三者构成等比数列.
②数列 中,
中, =4
=4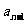 +1 (
+1 ( )且
)且 =1,若
=1,若 ,求证:数列{
,求证:数列{ }是等比数列。
}是等比数列。
(2)等比数列的通项:
(2009广东卷理)已知等比数列 满足
满足 ,且
,且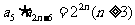 ,则当
,则当 时,
时,
A.
 B.
B.  C.
C.  D.
D.

[解析]由 得
得 ,
, ,则
,则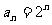 ,
, 
 ,选C.
,选C.
(3)等比数列的前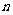 和:
和:
(1)等比数列中, =2,S99=77,求
=2,S99=77,求 (答:44);
(答:44);
(2) 的值为__________(答:2046);
的值为__________(答:2046);
(4)等比中项:
①已知两个正数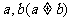 的等差中项为A,等比中项为B,则A与B的大小关系为______(答:A>B)
的等差中项为A,等比中项为B,则A与B的大小关系为______(答:A>B)
⑵(2009四川卷文)等差数列{ }的公差不为零,首项
}的公差不为零,首项 =1,
=1, 是
是 和
和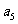 的等比中项,则数列的前10项之和是
的等比中项,则数列的前10项之和是
A. 90 B. 100 C. 145 D. 190 .
[答案]B
[解析]设公差为 ,则
,则 .∵
.∵ ≠0,解得
≠0,解得 =2,∴
=2,∴ =100
=100
③(2009江西卷文)公差不为零的等差数列 的前
的前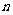 项和为
项和为 .若
.若 是
是 的等比中项,
的等比中项,  ,则
,则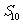 等于
等于
A. 18 B. 24 C. 60 D. 90 .
答案:C
[解析]由 得
得 得
得 ,再由
,再由 得
得
 则
则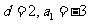 ,所以
,所以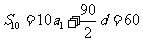 ,.故选C
,.故选C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com