
16、(1)证明: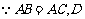 为
为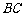 中点,
中点,
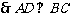 ,
,
又直三棱柱中: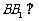 底面
底面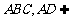 底面
底面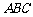 ,
,
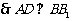 ,
,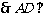 平面
平面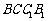 ,
,

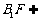 平面
平面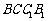 ,
,
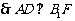 .
.
在 矩形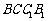 中:
中: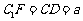 ,
,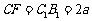 ,
,
 ,
,
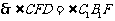 ,
,
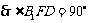 ,即
,即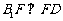 ,
,
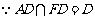 ,
,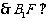 平面
平面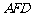 ;-----------5分
;-----------5分
(2)解:
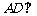 平面
平面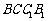 ,
,
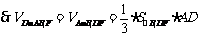 =
=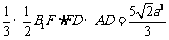 ; -------10分
; -------10分
(3)当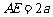 时,
时,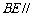 平面
平面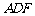 .
.
证明:连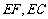 ,设
,设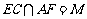 ,连
,连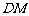 ,
,
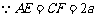 ,
,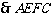 为矩形,
为矩形,
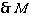 为
为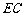 中点,
中点,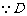 为
为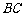 中点,
中点,
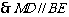 ,
,
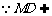 平面
平面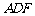 ,
,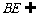 平面
平面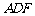 ,
,
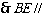 平面
平面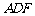 .
-------15分
.
-------15分
15、(1)n≥2时,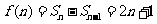 . ………………… 4分
. ………………… 4分
n=1时,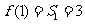 ,适合上式,
,适合上式,
∴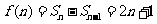
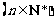 .
………………… 5分
.
………………… 5分
(2)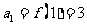 ,
,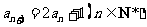 .
………………… 8分
.
………………… 8分
即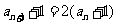 .
.
∴数列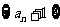 是首项为4、公比为2的等比数列. ………………… 10分
是首项为4、公比为2的等比数列. ………………… 10分
 ,∴
,∴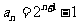
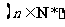 .……………… 12分
.……………… 12分
Tn=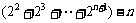 =
=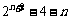 .
………………… 14分
.
………………… 14分
13、y2=8x(x>0)或y=0 (x<0);14、7.
7、充分不必要;8、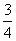 ;9、3;10、
;9、3;10、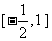 ;11、3;12、
;11、3;12、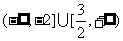 ;
;
1、16;2、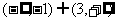 ;3、
;3、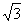 ;4、
;4、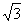 ;5、
;5、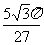 ;6、
;6、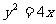 ;
;
16、在直三棱柱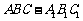 中,
中,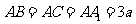 ,
,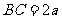 ,
,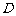 是
是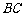 的中点,
的中点,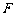 是
是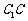 上一点,且
上一点,且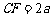 .
.
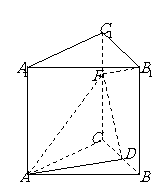 (1)求证:
(1)求证: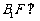 平面
平面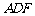 ;(2)求三棱锥
;(2)求三棱锥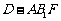 的体积;
的体积;
(3)试在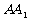 上找一点
上找一点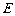 ,使得
,使得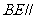 平面
平面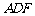 .
.
15、已知数列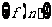 的前n项和为
的前n项和为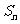 ,且
,且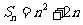 .
.
(Ⅰ)求数列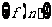 通项公式;(Ⅱ)若
通项公式;(Ⅱ)若 ,
,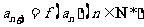 ,求证数列
,求证数列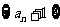 是等比数列,并求数列
是等比数列,并求数列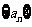 的前
的前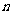 项和
项和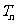 .
.
14、设集合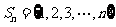 ,若
,若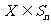 ,把
,把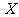 的所有元素的乘积称为
的所有元素的乘积称为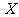 的容量(若
的容量(若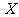 中只有一个元素,则该元素的数值即为它的容量,规定空集的容量为0)。若
中只有一个元素,则该元素的数值即为它的容量,规定空集的容量为0)。若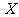 的容量为奇(偶)数,则称
的容量为奇(偶)数,则称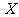 为
为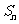 的奇(偶)子集。若
的奇(偶)子集。若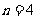 ,则
,则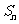 的所有奇子集的容量之和为____ .
的所有奇子集的容量之和为____ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com