
21.(本题15分)
(Ⅰ)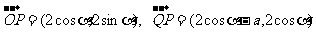 ,由OP⊥PQ,得
,由OP⊥PQ,得
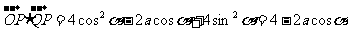 =0,
=0,
由 ,得得cosa =
,得得cosa = 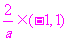 ,
,
a < –2或a >2. 7分
(Ⅱ)(向量坐标法)当a= –1时, 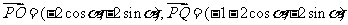 ,
,
 (第21题) |
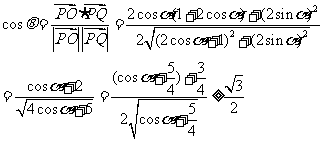
当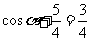 ,即
,即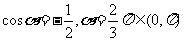 时,取等号.
时,取等号.
又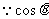 在
在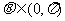 上是减函数,
上是减函数, .
8分
.
8分
另解:(余弦定理法).如图,  ,
,
设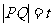 ,则
,则 ,
,
又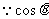 在
在 上是减函数,
上是减函数, ,
,
此时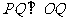 ,
,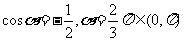 8分
8分
20.(本题14分)(Ⅰ)在等差数列 中,由
中,由
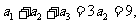 得,
得,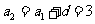
又由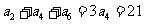 ,得
,得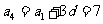 ,
,
联立解得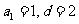 , 3分
, 3分
则数列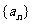 的通项公式为
的通项公式为
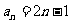 .
3分
.
3分
(Ⅱ)
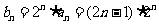 ,
,
∴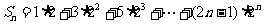 ……(1)
……(1)
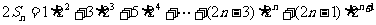 …(2)
…(2)
(1)、(2)两式相减,

得 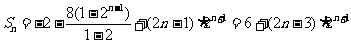 8分
8分
19.(本题14分)
(Ⅰ)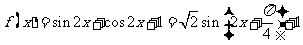 ,其最小正周期是
,其最小正周期是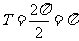 ,
,
又当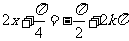 ,即
,即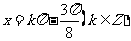 时,
时, 取得最小值
取得最小值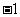 ,
,
所以函数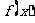 的最小值是
的最小值是 ,此时
,此时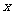 的集合为
的集合为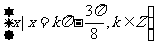 .
7分
.
7分
(Ⅱ)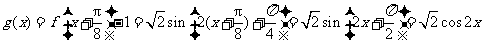

 .
.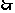 函数
函数 是偶函数. 7分
是偶函数. 7分
18.(本题14分)
(Ⅰ)第1次摸球有4个可能的结果:a,b,c,d,其中第1次摸到黄球的结果包括:a,b,故第1次摸到黄球的概率是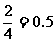 . 4分
. 4分
(Ⅱ)先后两次摸球有12种可能的结果:(a,b)(a,c)(a,d)(b,a)(b,c)(b,d)(c,a)(c,b)(c,d)(d,a)(d,b)(d,c),其中第2次摸到黄球的结果包括:(a,b)(b,a)(c,a)(c,b)(d,a)(d,b),故第2次摸到黄球的概率为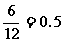 . 10分
. 10分
11.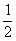 12.
12.  13. x = 1 14. 224 15.0 16.
13. x = 1 14. 224 15.0 16. 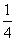 17.
3600
17.
3600
22. (本题15分)已知函数 .
.
(I)若函数 在点
在点 处的切线斜率为4,求实数
处的切线斜率为4,求实数 的值;
的值;
(II)若函数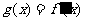 在区间
在区间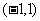 上存在零点,求实数
上存在零点,求实数 的取值范围.
的取值范围.
2010年杭州市第一次高考科目教学质量检测数学文科评分标准
21.(本题15分)已知点 和Q( a,0 ),
和Q( a,0 ),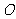 为坐标原点.当
为坐标原点.当 时.
时.
(Ⅰ)若存在点P,使得OP⊥PQ,求实数a的取值范围;
(Ⅱ) 如果a = –1,求向量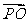 与
与 的夹角
的夹角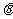 的最大值.
的最大值.
20.(本题14分)在等差数列 中,已知
中,已知 ,
,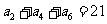 .
.
(Ⅰ)求数列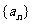 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前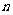 项和
项和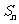 .
.
19.(本题14分)已知函数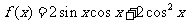 (
(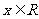 ).
).
(Ⅰ)求 的最小正周期,并求
的最小正周期,并求 的最小值;
的最小值;
(Ⅱ)令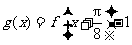 ,判断函数
,判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
18.(本题14分)从装有编号分别为a,b的2个黄球和编号分别为 c,d的2个红球的袋中无放回地摸球,每次任摸一球,求:
(Ⅰ)第1次摸到黄球的概率;
(Ⅱ)第2次摸到黄球的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com