
2.下列有关细胞生命活动的分析正确的是
A.无线粒体的细胞可在质膜上进行需氧呼吸
B.将原生质体放入高渗溶液中可观察到质壁分离现象
C.与抗体分泌有关的细胞器有核糖体、线粒体、内质网、高尔基体、中心体
D.胞吐要消耗能量,因此经胞吐出细胞的物质的转运方式是主动转运
1.某池塘中,早期藻类大量繁殖,食藻浮游动物水蚤大量繁殖,藻类减少,接着又引起水蚤减少。后期排入污水,引起部分水蚤死亡,加重了污染,导致更多水蚤死亡。关于上述过程的叙述,正确的是
A.早期不属于负反馈,后期属于负反馈 B.早期属于负反馈,后期属于正反馈
C.早期、后期均属于负反馈 D.早期、后期均属于正反馈
22.(本题15分).
(Ⅰ)由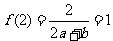 ,得
,得 ;又
;又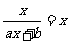 有且仅有一个解,即
有且仅有一个解,即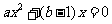 有唯一解满足
有唯一解满足 .
.
 当
当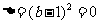 时,
时,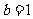 ,
,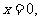 则
则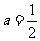 ,此时
,此时
又当 时,
时, ,因为
,因为 ,
,
所以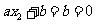 ,则
,则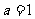 ,此时
,此时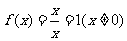
综上所述, 或者
或者 ;
4分
;
4分
(Ⅱ) 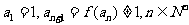 ,当
,当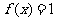 时,
时,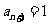 ,不合题意,
,不合题意,
则 ,
,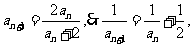 则
则 ,
,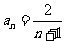 4分
4分
(Ⅲ)由(Ⅱ)知,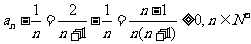
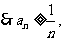 则
则 ,所以
,所以 2分
2分
设数列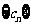 的前
的前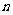 项和为
项和为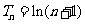 ,则
,则
当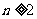 时,
时,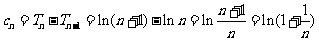 ,要证明
,要证明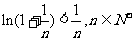
令 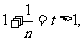 只要证明:
只要证明: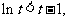 其中
其中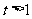 .
.
令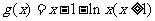 ,则
,则 ,所以
,所以 在
在 上是增函数,
上是增函数,
则当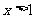 时,
时,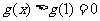 ,即
,即 ,所以
,所以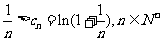 ,
,
则  . 5分
. 5分
[说明]也可用数学归纳法证明,为此,先证明 即证:
即证: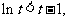 其中
其中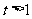 .
.

21.(本题15分)
(Ⅰ)当A、D区域同时用红色鲜花时,其它区域不能用红色.
 (第21题) |
因此,布置花圃的不同方法的种数为4´3´3 = 36种.… ………………4分
(穷举全部情况满分,部分情况酌情给分)
(Ⅱ)设M表示事件“恰有两个区域用红色鲜花”,
当区域A、D同色时,共有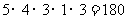 种;
种;
当区域A、D不同色时,共有 种;
种;
因此,所有基本事件总数为:180+240=420种(是等可能的)……2分
又因为A、D为红色时,共有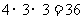 种;
种;
B、E为红色时,共有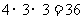 种;
种;
因此,事件M包含的基本事件有:36+36=72种.
所以,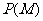 =
=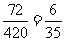 .
……………………………………………3分
.
……………………………………………3分
(Ⅲ)随机变量 的分布列为:
的分布列为:
 |
0 |
1 |
2 |
|
P |
 |
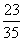 |
 |
所以, =
= .……………………………………6分
.……………………………………6分
20.(本题14分)由题意得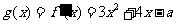 .
.
(I) 4分
4分
(II)讨论:(1)当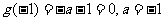 时,
时,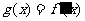 的零点
的零点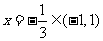 ;
;
(2)当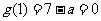 时,
时,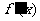 的零点
的零点 ,不合题意; 3分
,不合题意; 3分
(3)当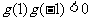 时,
时,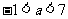
(4)当 时,
时,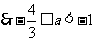
综上所述,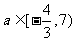 7分
7分
(II)另解: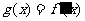 在区间
在区间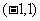 上存在零点,等价于
上存在零点,等价于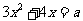 在区间
在区间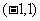 上有解,
上有解,
也等价于直线 与曲线
与曲线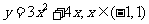 有公共点,
有公共点,
作图可得 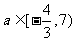 . 7分
. 7分
或者:又等价于当 时
,求值域:
时
,求值域: . 7分
. 7分
19.(本题14分)(Ⅰ)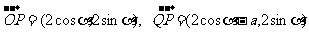 ,由OP⊥PQ,得
,由OP⊥PQ,得
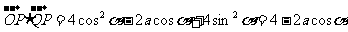 =0,
=0,
由 ,得cosa =
,得cosa =  ,
,
解得a < –2或a >2. 7分
(Ⅱ)(向量坐标法)当a= –1时,
 ,
,
|
(第19题) |
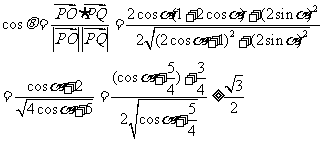
当 ,即
,即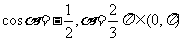 时,取等号.
7分
时,取等号.
7分

另证(余弦定理).如图,  ,
,
设 ,则
,则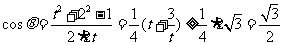 ,
,
取等号时,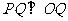 ,
,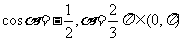 7分
7分
18.(本题14分)
(Ⅰ)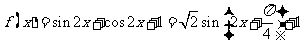 ,其最小正周期是
,其最小正周期是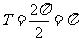 ,
,
又当 ,即
,即 时,
时,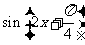 取得最小值
取得最小值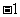 ,
,
所以函数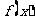 的最小值是
的最小值是 ,此时
,此时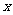 的集合为
的集合为 . 6分
. 6分
(Ⅱ)
由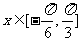 ,得
,得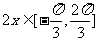 ,则
,则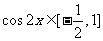 ,
,
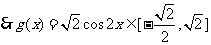 ,
,
若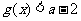 对于
对于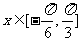 恒成立,则
恒成立,则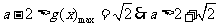 8分
8分
11. 90° 12. x =
1 13. 224 14. 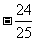 15. 0 16.
3465 17.[– 1,7]
15. 0 16.
3465 17.[– 1,7]
22.(本题15分)已知函数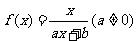 满足
满足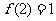 ,且方程f(x) = x有且仅有一个实数根.
,且方程f(x) = x有且仅有一个实数根.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)设数列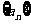 满足
满足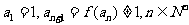 .求数列
.求数列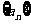 的通项公式;
的通项公式;
(Ⅲ)定义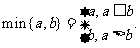 对于(Ⅱ)中的数列
对于(Ⅱ)中的数列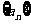 ,令
,令  设
设 为数列
为数列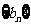 的前
的前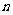 项和,求证:
项和,求证: .
.
2010年杭州市第一次高考科目教学质量检测数学理科评分标准
21.(本题15分)某学校要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
(Ⅰ)当A、D区域同时用红色鲜花时,求布置花圃的不同方法的种数;
 (第21题) |
(Ⅱ)求恰有两个区域用红色鲜花的概率;
(Ⅲ)记 为花圃中用红色鲜花布置的区域的个数,求随机变量
为花圃中用红色鲜花布置的区域的个数,求随机变量 的分布列及其数学期望E
的分布列及其数学期望E .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com